
12 Caractéristiques des ondes (avec exemples)

le caractéristiques des vagues sont les caractéristiques du phénomène ondulatoire: longueur d'onde, fréquence, vallées, crêtes, vitesse, énergie et autres que nous expliquerons dans cet article.
Dans les ondes, ce ne sont pas les particules qui voyagent avec la perturbation, mais l'énergie. Lorsqu'une onde se propage dans un milieu matériel, qui peut être de l'eau, de l'air ou une corde, entre autres, les particules se déplacent à peine de la position d'équilibre, pour y revenir après un court laps de temps.
Cependant, le mouvement est transmis d'une particule à une autre, faisant vibrer chacune d'elles. De cette façon, la perturbation que nous appelons vague, tout comme la vague de supporters dans les stades, lorsque les matchs de football sont joués.
L'étude des vagues est très intéressante, car nous vivons dans un monde qui en regorge: la lumière, les vagues de la mer, le son de la musique et la voix sont tous des phénomènes ondulatoires, bien que de nature différente. La lumière et le son sont particulièrement importants, car nous en avons constamment besoin pour communiquer avec le monde extérieur..
Quelles sont les caractéristiques des vagues?
Vibration
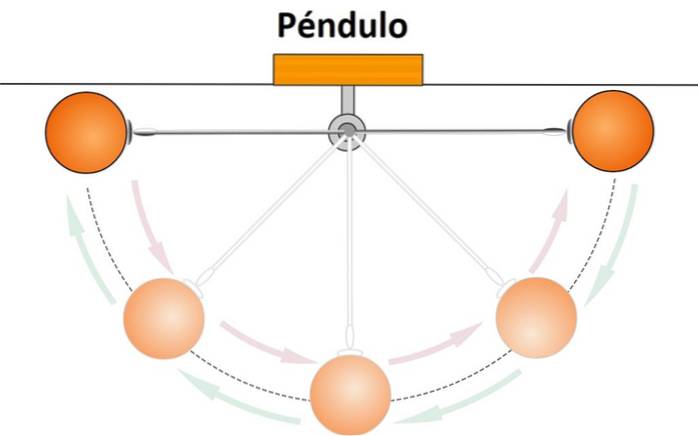
C'est le chemin complet qu'une particule effectue dans son mouvement de va-et-vient. Par exemple, un pendule a un mouvement de va-et-vient, car à partir d'un certain point, il décrit un arc, s'arrête lorsqu'il atteint une certaine hauteur et revient à sa position d'origine..
S'il n'y avait pas de friction, ce mouvement se poursuivrait indéfiniment. Mais à cause du frottement, le mouvement devient plus lent et moins large, jusqu'à ce que le pendule s'arrête..
Lorsqu'une corde horizontale tendue est perturbée, les particules de la corde vibrent dans le sens vertical, c'est-à-dire de haut en bas, tandis que la perturbation se déplace horizontalement le long de la corde.
Centre de balançoire
Lorsqu'une particule effectue son mouvement de va-et-vient, elle le fait en se déplaçant autour d'un certain point, appelé origine ou centre d'oscillation..
Dans l'exemple du pendule, il est en équilibre au point le plus bas, et il oscille autour de lui si on le sépare un peu de cette position. Par conséquent, ce point peut être considéré comme le centre de l'oscillation.
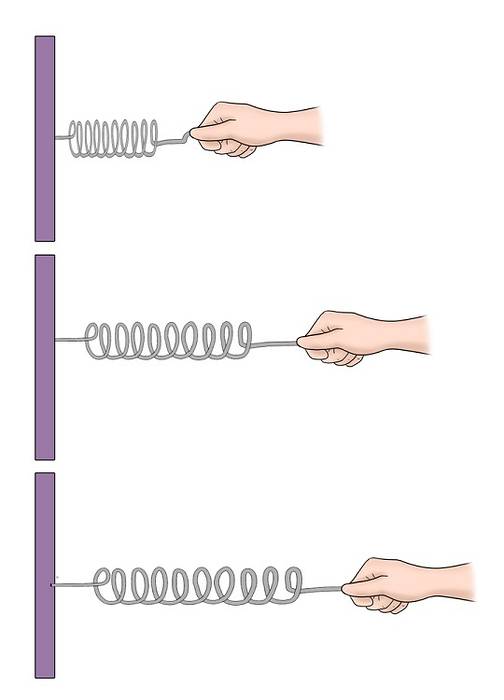
On peut aussi imaginer un ressort sur une table horizontale, attaché à une extrémité à un mur, et avec un bloc à l'autre extrémité. Si le système de bloc à ressort n'est pas perturbé, le bloc est dans une certaine position d'équilibre.
Cependant, en comprimant ou en étirant un peu le ressort, le système commence à osciller autour de cette position d'équilibre..
Élongation
C'est la distance à laquelle la particule s'éloigne du centre d'oscillation après un certain temps. Il est mesuré en mètres lorsque le système international SI est utilisé..
Si un ressort avec un bloc à une extrémité est comprimé ou étiré, on dit qu'il a subi un allongement d'un nombre "x" de mètres, de centimètres ou de toute autre unité utilisée pour mesurer la distance..
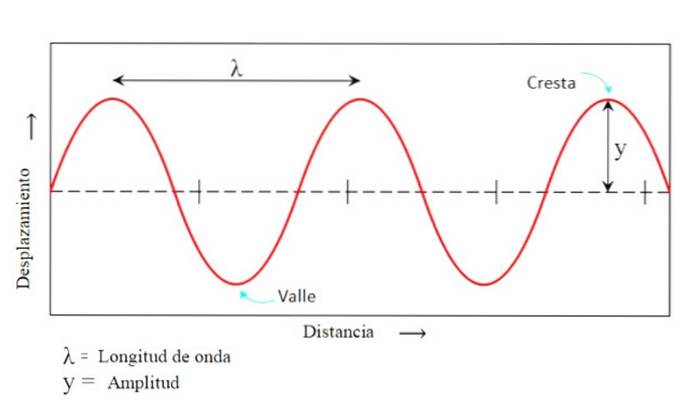
Crêtes et vallées
Ce sont respectivement les points les plus hauts et les plus bas que la particule atteint par rapport à la position d'équilibre y = 0 (voir figure 1).
Amplitude

C'est la distance maximale que la particule sépare du centre d'oscillation et est également donnée en mètres. Il est noté À ou comment Oui. Là, la position d'équilibre coïncide avec y = 0 et correspond aux crêtes et vallées de la vague.
L'amplitude est un paramètre important, car elle est liée à l'énergie transportée par l'onde. Plus l'amplitude est grande, plus l'énergie est grande, comme c'est le cas avec les vagues de l'océan, par exemple.
Nœud
Les nœuds sont les points où la particule passe par le centre d'oscillation ou la position d'équilibre..
Cycle
C'est ce qu'on appelle une oscillation complète, lorsque la particule passe d'une crête à l'autre, ou d'une vallée à l'autre. Alors on dit que ça a pédalé.
Le pendule exécute un balancement complet lorsqu'il s'éloigne d'une certaine hauteur de la position d'équilibre, passe par le point le plus bas, monte à la même hauteur à l'aller et revient à la hauteur initiale lors du voyage de retour.
Période
Les ondes étant répétitives, le mouvement des particules est périodique. La période est le temps nécessaire pour effectuer une oscillation complète et est généralement indiquée par la lettre majuscule T. Les unités de la période dans le SI International System sont les secondes.
La fréquence
C'est la grandeur inverse ou réciproque de la période et est liée au nombre d'oscillations ou de cycles effectués par unité de temps. Il est indiqué par la lettre F.
Le nombre d'oscillations n'étant pas une unité, les secondes sont utilisées pour la fréquence-1 (s-1), appelé Hertz ou hertz et en abrégé Hz.
Étant l'inverse de la période, nous pouvons écrire une relation mathématique entre les deux grandeurs:
f = 1 / T
Ou bien:
T = 1 / f
Si, par exemple, un pendule exécute 30 cycles en 6 secondes, sa fréquence est:
f = (30 cycles) / (6 s) = 5 cycles / s = 5 Hz.
Longueur d'onde
C'est la distance entre deux points d'une vague qui sont à la même hauteur, à condition qu'une oscillation complète ait été faite. Il peut être mesuré d'une crête à une autre d'affilée, par exemple, mais aussi de vallée en vallée.
La longueur d'onde est désignée par la lettre grecque λ, qui se lit «lambda» et est mesurée en unités de distance telles que les mètres dans le système international, bien qu'il y ait une si grande variété de longueurs d'onde que les multiples et sous-multiples sont fréquents.
Numéro d'onde
C'est la magnitude inverse de la longueur d'onde, multipliée par le nombre 2π. Par conséquent, en désignant le nombre d'onde par la lettre k, nous avons:
k = 2π / λ
Vitesse de propagation
C'est la vitesse à laquelle la perturbation se déplace. Si le milieu dans lequel se propage l'onde est homogène et isotrope, c'est-à-dire que ses propriétés sont les mêmes partout, alors cette vitesse est constante et est donnée par:
v = λ / T
Les unités de vitesse de propagation sont les mêmes que pour toute autre vitesse. Dans le système international, cela correspond à m / s.
Puisque la période est l'inverse de la fréquence, elle peut également être exprimée:
v = λ. F
Et comme la vitesse est constante, le produit λ.f est également constant, de sorte que si, par exemple, la longueur d'onde est modifiée, la fréquence change pour que le produit reste le même.
Les références
- Giancoli, D. 2006. Physique: principes avec applications. 6e. Salle des Prentices Ed.
- Hewitt, Paul. 2012. Science physique conceptuelle. 5ème. Ed. Pearson.
- Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 1. Pearson.
- Serway, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Éd. Cengage Learning.
- Tipler, P. (2006) Physique pour la science et la technologie. 5e éd. Volume 1. Éditorial Reverté.



Personne n'a encore commenté ce post.