La accélération instantanée C'est le changement que subit la vitesse par unité de temps à chaque instant du mouvement. Au moment précis où le "dragster«De l'image photographiée, elle portait une accélération de 29,4 m / sdeux. Cela signifie qu'à ce moment-là, sa vitesse était augmentée de 29,4 m / s en l'espace de 1 s. Cela équivaut à 105 km / h en seulement 1 seconde.
Une compétition de dragsters est facilement modélisée en supposant que la voiture de course est un objet ponctuel. P qui se déplace en ligne droite. Sur cette ligne un axe orienté avec l'origine est choisi OU ALORS que nous appellerons l'axeBŒUF) ou juste axe X.
Les variables cinématiques qui définissent et décrivent le mouvement sont:
Ce sont toutes des quantités vectorielles. Par conséquent, ils ont une grandeur, une direction et un sens.
Dans le cas d'un mouvement rectiligne, il n'y a que deux directions possibles: positive (+) dans la direction de (BŒUF) ou négatif (-) dans le sens opposé de (BŒUF). Par conséquent, il est possible de se passer de la notation vectorielle formelle et d'utiliser les signes pour indiquer le sens de la grandeur.
Index des articles
Supposons qu'à l'instant t la particule a de la vitesse v (t) et dans l'instant t ' sa vitesse est v (t ').
Ainsi, le changement que la vitesse a eu pendant cette période était Δv = v (t ') - v (t). D'où l'accélération dans le laps de temps Δt = t '- t , serait donné par le quotient:
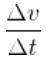
Ce quotient est l'accélération moyenne àm dans la période de temps Δt entre les instants t et t '.
Si nous voulions calculer l'accélération juste au temps t, alors t 'devrait être une quantité insignifiante plus grande que t. Avec ce Δt, qui est la différence entre les deux, devrait être presque nul.
Mathématiquement, il est indiqué comme suit: Δt → 0 et il est obtenu:
JE) Une particule se déplace le long de l'axe X avec une vitesse constante v0 = 3 m / s. Quelle sera l'accélération de la particule?
La dérivée d'une constante est nulle, donc l'accélération d'une particule se déplaçant à vitesse constante est nulle.
II) Une particule se déplace sur l'axe X et sa vitesse change avec le temps selon la formule suivante:
v (t) = 2 - 3t
Où la vitesse est mesurée en m / s et le temps en s. Quelle sera l'accélération de la particule?
)
Le résultat est interprété comme ceci: pour tout instant l'accélération est de -3 m / s.
Entre les instants 0 s et 2/3 s la vitesse est positive tandis que l'accélération est négative, c'est-à-dire que dans cet intervalle la particule diminue sa vitesse ou décélère.
A l'instant 2/3 s, sa vitesse devient nulle, mais comme il reste une accélération de -3 m / s, à partir de cet instant la vitesse s'inverse (elle devient négative).
Dans les instants après ⅔ s, la particule accélère, puisque chaque fois que sa vitesse devient plus négative, c'est-à-dire que sa vitesse (module de vitesse) augmente.
III) La figure montre une courbe qui représente la vitesse en fonction du temps, pour une particule qui se déplace le long de l'axe X. Trouvez le signe de l'accélération aux instants t1, tdeux et toi3. Indiquez également si la particule accélère ou décélère.
L'accélération est la dérivée de la fonction de vitesse, elle équivaut donc à la pente de la tangente à la courbe v (t) pour un instant t donné.
Pour l'instant t1, la pente est négative, donc l'accélération est négative. Et comme à cet instant la vitesse est positive, on peut affirmer qu'à cet instant la particule décélère.
Pour l'instant tdeux la ligne tangente à la courbe v (t) est horizontale, donc sa pente est nulle. Le mobile a une accélération nulle, donc à tdeux la particule n'accélère ni ne décélère.
Pour l'instant t3, la pente de la tangente à la courbe v (t) est positive. Avec une accélération positive, la particule accélère vraiment, car à ce moment la vitesse est également positive.
Dans la section précédente, l'accélération instantanée était définie à partir de la vitesse instantanée. En d'autres termes, si la vitesse est connue à chaque instant, alors il est également possible de connaître l'accélération à chaque instant du mouvement..
Le processus inverse est possible. Autrement dit, connaissant l'accélération pour chaque instant, la vitesse instantanée peut être calculée.
Si l'opération qui permet de passer de la vitesse à l'accélération est la dérivée, l'opération mathématique inverse est l'intégration.
L'accélération d'une particule se déplaçant le long de l'axe X est a (t) = ¼ tdeux. Où t est mesuré en secondes et a en m / s. Déterminer l'accélération et la vitesse de la particule à 2 s de mouvement, sachant qu'à l'instant initial t0 = 0 était au repos.
À 2 s l'accélération est de 1 m / sdeux et la vitesse pour l'instant t sera donnée par:
Un objet se déplace le long de l'axe X avec une vitesse en m / s, donnée par:
v (t) = 3 tdeux - 2 t, où t est mesuré en secondes. Déterminez l'accélération aux moments: 0s, 1s, 3s.
En prenant la dérivée de v (t) par rapport à t, l'accélération à tout instant est obtenue:
a (t) = 6t -2
Alors a (0) = -2 m / sdeux ; a (1) = 4 m / sdeux ; a (3) = 16 m / sdeux .
Une sphère métallique est libérée du haut d'un bâtiment. L'accélération descendante est l'accélération de la gravité qui peut être approximée par la valeur 10 m / s2 et pointant vers le bas. Déterminer la vitesse de la sphère 3 s après sa libération.
Ce problème implique l'accélération de la gravité. Prendre la direction verticale comme positive vers le bas, nous avons que l'accélération de la sphère est:
a (t) = 10 m / sdeux
Et la vitesse sera donnée par:
Une sphère métallique est projetée vers le haut avec une vitesse initiale de 30 m / s. L'accélération du mouvement est l'accélération de la pesanteur qui peut être approximée par la valeur 10 m / sdeux et pointant vers le bas. Déterminer la vitesse de la sphère à 2 s et 4 s après son tir.
La direction verticale sera considérée comme positive en haut. ETDans ce cas, l'accélération du mouvement sera donnée par
a (t) = -10 m / sdeux
La vitesse en fonction du temps sera donnée par:
Après 4 s de tir, la vitesse sera de 30 - 10 ∙ 4 = -10 m / s. Ce qui signifie qu'à 4 s la sphère descend avec une vitesse de 10 m / s.
Personne n'a encore commenté ce post.