Accélération moyenne comment elle est calculée et les exercices résolus

La accélération moyenne à_m C'est la grandeur qui décrit la variation de la vitesse d'une particule au cours du temps. C'est important, car cela montre les variations que le mouvement éprouve.

Pour exprimer cette grandeur en termes mathématiques, il faut considérer deux vitesses et deux instants de temps, qui sont respectivement notés v₁ et V_deux, et toi₁ et toi_deux.

En combinant les valeurs selon la définition proposée, l'expression suivante sera obtenue:

Dans le système SI international, les unités pour un_m sera m / s^deux, bien que d'autres unités impliquant la longueur par unité de temps au carré suffiront.

Par exemple, il y a le km / h.s qui se lit "kilomètre par heure et par seconde". Notez que l'unité de temps apparaît deux fois. En pensant à un mobile se déplaçant le long d'une ligne droite, cela signifie que pour chaque seconde écoulée, le mobile augmente sa vitesse de 1 km / h. Soit il le diminue de 1 km / h pour chaque seconde qui passe.

Index des articles

• 1 Accélération, vitesse et vitesse
• 2 Comment l'accélération moyenne est calculée
• 3 signes d'accélération dans le mouvement unidimensionnel
• 4 Chute libre: un mouvement à accélération constante
• 5 Exercice résolu
  • 5.1 Réponse
• 6 Références

Accélération, vitesse et vitesse

Bien que l'accélération soit associée à une augmentation de la vitesse, la vérité est qu'en observant attentivement la définition, il s'avère que tout changement de vitesse implique l'existence d'une accélération.

Et la vitesse ne change pas nécessairement toujours d'ampleur. Il peut arriver que le mobile change uniquement de direction et garde sa vitesse constante. Il y a toujours une accélération responsable de ce changement.

Un exemple de ceci est une voiture qui fait une courbe avec une vitesse constante de 60 km / h. Le véhicule est soumis à une accélération, qui est responsable du changement de direction de la vitesse afin que la voiture suive la courbe. Le conducteur l'applique à l'aide du volant.

Une telle accélération est dirigée vers le centre de la trajectoire courbe, pour empêcher la voiture d'en sortir. Il reçoit le nom d'accélération radial ou alors Ordinaire. Si l'accélération radiale était soudainement annulée, la voiture ne pourrait plus continuer à tourner autour de la courbe et continuerait en ligne droite.

Une voiture circulant autour d'une courbe est un exemple de mouvement en deux dimensions, alors que lorsqu'elle roule en ligne droite, son mouvement est unidimensionnel. Dans ce cas, le seul effet de l'accélération est de changer la vitesse de la voiture..

Cette accélération s'appelle l'accélération tangentiel. Ce n'est pas exclusif au mouvement unidimensionnel. La voiture faisant le tour de la courbe à 60 km / h pourrait en même temps accélérer à 70 km / h en la prenant. Dans ce cas, le conducteur doit utiliser à la fois le volant et la pédale d'accélérateur..

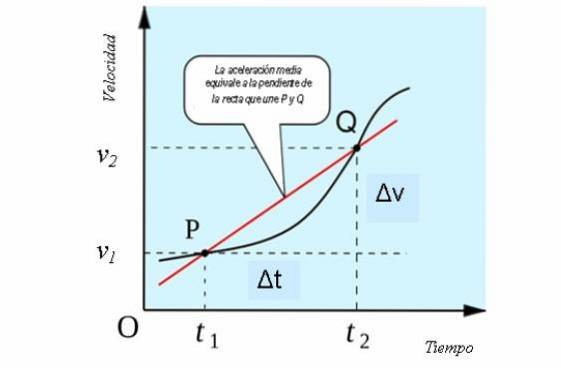
Si nous considérons un mouvement unidimensionnel, l'accélération moyenne a une interprétation géométrique similaire à celle de la vitesse moyenne, comme la pente de la ligne sécante qui coupe la courbe aux points P et Q du graphique vitesse en fonction du temps..

Cela peut être vu dans la figure suivante:

Comment l'accélération moyenne est calculée

Regardons quelques exemples pour calculer l'accélération moyenne dans diverses situations:

I) A un certain instant dans le temps, un mobile se déplaçant le long d'une ligne droite a une vitesse de + 25 km / h et 120 secondes plus tard, il en a une autre de -10 km / h. Quelle était l'accélération moyenne?

Répondre

Le mouvement étant unidimensionnel, la notation vectorielle peut être supprimée, auquel cas:

v_{ou alors} = +25 km / h = +6,94 m / s

v_F = -10 km / h = - 2,78 m / s

Δt = 120 s

Chaque fois que vous avez un exercice avec des magnitudes mixtes comme celui-ci, dans lequel il y a des heures et des secondes, il est nécessaire de passer toutes les valeurs aux mêmes unités.

Étant un mouvement unidimensionnel, la notation vectorielle a été supprimée.

II) Un cycliste se déplace vers l'est à une vitesse de 2,6 m / s et 5 minutes plus tard vers le sud à 1,8 m / s. Trouvez son accélération moyenne.

Répondre

Le mouvement ne pas il est unidimensionnel, c'est pourquoi la notation vectorielle est utilisée. Les vecteurs unitaires je Oui j indiquer les directions avec la convention de signe suivante, facilitant le calcul:

• Nord: +j
• Sud: -j
• Est: +je
• Ouest: -je

v_deux = - 1,8 j Mme

v₁ = + 2,6 je Mme

Δt = 5 minutes = 300 secondes

Signes d'accélération dans le mouvement unidimensionnel

Comme toujours avec des grandeurs moyennes ou moyennes, les informations fournies sont globales. Ils n'offrent pas de détails sur ce qui est arrivé au mobile à chaque instant, cependant ce qu'ils apportent est toujours précieux pour la description du mouvement..

En utilisant à la fois les signes de vitesse et d'accélération, il est possible de savoir si un mobile se déplaçant en ligne droite accélère ou ralentit. Dans les deux situations, l'accélération est présente, car la vitesse change.

Voici quelques considérations intéressantes concernant les signes de ces deux quantités:

• La vitesse et l'accélération moyennes, toutes deux du même signe, signifient que, globalement, le mobile va de plus en plus vite.
• La vitesse et l'accélération avec des signes différents sont le signe d'un mobile qui a plutôt freiné.

On pense généralement que chaque fois qu'il s'agit d'une accélération négative, le mobile freine. Cela est vrai si la vitesse du mobile est positive. Mais s'il est négatif, la vitesse augmente en fait.

Comme toujours lorsque vous étudiez le mouvement, pensez à des cas particuliers. Par exemple, que se passe-t-il lorsque l'accélération moyenne est nulle? Cela signifie-t-il que le mobile a toujours maintenu sa vitesse constante??

La réponse est non. Le mobile aurait pu faire varier sa vitesse dans l'intervalle considéré, mais les vitesses initiale et finale étaient les mêmes. Pour le moment, les détails de ce qui s'est passé dans l'intervalle sont inconnus, car l'accélération moyenne n'offre pas plus d'informations.

Et si l'accélération moyenne à_m équivaut à une accélération à à tout moment dans l'intervalle de temps? Il s'agit d'une situation très intéressante appelée mouvement rectiligne à variation uniforme ou MRUV en abrégé..

Cela signifie que la vitesse change uniformément au fil du temps. Par conséquent, l'accélération est constante. Dans la nature, il existe un tel mouvement, que tout le monde connaît: la chute libre.

Chute libre: un mouvement à accélération constante

C'est un fait connu que la terre attire des objets vers son centre et que lorsque l'on est relâché à une certaine hauteur, elle subit l'accélération de la pesanteur, dont la valeur est approximativement constante et égale à 9,8 m / s.^deux près de la surface.

Si la résistance de l'air n'intervient pas, le mouvement est vertical et est appelé chute libre. Lorsque l'accélération est constante et en choisissant t₀ = 0, l'équation de l'accélération moyenne devient:

v_F = v₀ + à = gt (v₀= 0)

Où a = g = 9,8 m / s^deux

Exercice résolu

Un objet tombe d'une hauteur suffisante. Trouver la vitesse après 1,25 seconde.

Répondre

v_{ou alors} = 0, puisque l'objet est déposé, alors:

v_F = gt = 9,8 x 1,25 m / s = 12,25 m / s, orienté verticalement vers le sol. (La direction verticale descendante a été considérée comme positive).

Lorsque l'objet s'approche du sol, sa vitesse augmente de 9,8 m / s pour chaque seconde écoulée. La masse de l'objet n'est pas impliquée. Deux objets différents, tombés de la même hauteur et en même temps, développent la même vitesse lorsqu'ils tombent.

Les références

1. Giancoli, D. Physique. Principes avec applications. Sixième édition. Prentice Hall. 21 à 35.
2. Resnick, R. (1999). Physique. Volume 1. Troisième édition en espagnol. Mexique. Compañía Editorial Continental S.A. de C.V. 20-34.
3. Serway, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7^ma. Édition. Mexique. Éditeurs d'apprentissage Cengage. 21-39.