
Formules d'accélération négative, calculs et exercices résolus
La accélération négative Il survient lorsque le changement ou la variation de la vitesse pendant une période de temps a un signe négatif. Observez le chien sur l'image en train de s'amuser sur la plage. Le sable ralentit son mouvement, ce qui signifie qu'il y a une accélération opposée à la vitesse qu'il porte.
Cette accélération peut être considérée comme négative, par opposition à la vitesse, qui est déclarée positive. Bien qu'une accélération négative n'entraîne pas toujours une réduction de vitesse.

Dans un mouvement unidimensionnel, la direction d'avance est généralement prise comme positive, c'est-à-dire la direction de la vitesse. C'est ce qui a été considéré précédemment: chez le chien de la figure, la direction positive est celle qui va de la queue à la tête.
Avant de s'enfoncer les pattes dans le sable, le chien est venu avec une certaine vitesse v en avant, c'est positif. Ensuite, le sable diminue sa vitesse jusqu'à ce qu'il s'arrête, c'est-à-dire une vitesse finale nulle.
Supposons que tout cela se soit produit dans un laps de temps Δt. L'accélération pendant ce temps sera calculée comme ceci:
a = (0 - v) ÷ Δt
Dans l'équation ci-dessus v> 0, Δt> 0 alors a < 0, es decir aceleración negativa (à < 0). Étant donné que la direction de la vitesse au départ a été considérée comme positive, une accélération négative signifie que l'accélération est dirigée loin de la vitesse. Par conséquent, il est conclu que:
Chaque fois que l'accélération d'un corps en mouvement pointe dans la direction opposée à la vitesse, le corps freine ou décélère.
Par conséquent, nous pouvons établir que:
- Lorsque la vitesse et l'accélération ont le même signe, quel que soit le signe, la vitesse augmente. Dans ce cas, la vitesse devient plus positive ou plus négative, selon le cas..
- Lorsque la vitesse et l'accélération ont des signes opposés, la vitesse diminue.
Index des articles
- 1 Formules de calcul de l'accélération
- 1.1 -Exemple 1
- 1.2 -Exemple 2
- 1.3 -Exemple 3-Le jet vertical
- 2 Références
Formules de calcul de l'accélération
Quel que soit le signe, l'accélération moyenne àm entre les moments t Oui t ' est calculé à l'aide de la formule suivante:
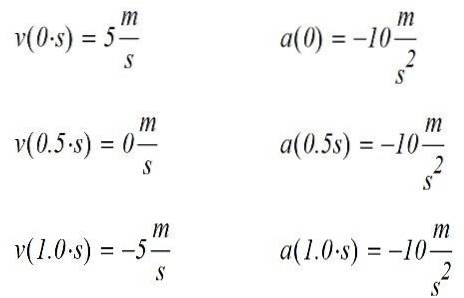
L'accélération moyenne fournit des informations globales sur l'évolution de la vitesse dans l'intervalle de temps considéré. D'autre part, l'accélération instantanée offre le détail de l'évolution de la vitesse à chaque instant. Ainsi pour un instant t donné, l'accélération est calculée par la formule suivante:
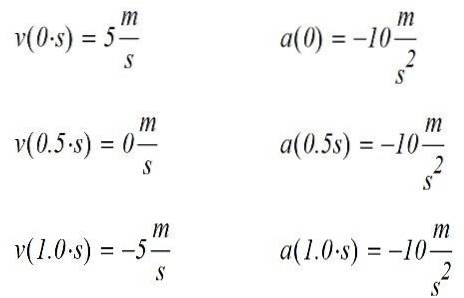
-Exemple 1
A l'instant initial t = 0,2 s un objet a une vitesse de 3 m / s. Plus tard, à l'instant t '= 0,4 s, il a une vitesse de 1 m / s. Calculer l'accélération moyenne entre les instants t et t 'et interpréter le résultat.
Répondre
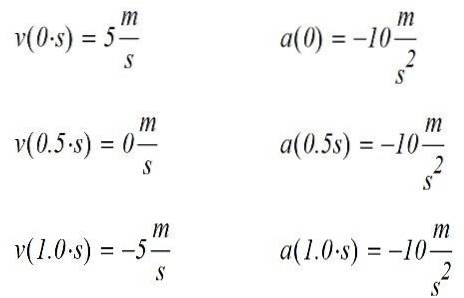
-Exemple 2
À l'instant initial t = 0,6 s, un objet a une vitesse de -1 m / s. Plus tard, à l'instant t '= 0,8 s, il a une vitesse de -3 m / s. Calculez l'accélération moyenne entre les instants t et t '. Interpréter le résultat.
Répondre
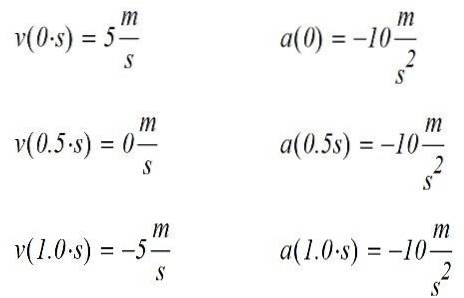
En conclusion, à la fin de l'intervalle de temps la vitesse est devenue encore plus négative (-3m / s).
Cela signifie-t-il que le mobile ralentit son mouvement? Non. Le signe moins dans la vitesse signifie seulement qu'il va en arrière et plus vite, car aller à -3 m / s va plus vite qu'à -1m / s, la vitesse qui était au début.
La vitesse, qui est le module de la vitesse, a augmenté malgré une accélération négative. Je veux dire, cet objet a accéléré. Par conséquent, nous concluons:
Tant que l'accélération d'un corps en mouvement pointe dans une direction parallèle à la vitesse, le corps accélère.
-Exemple 3 - Le vomissement vertical
Prenons l'exemple suivant: un objet a une vitesse instantanée donnée par l'expression suivante, avec toutes les unités du système international:
v (t) = 5 à 10 t
Trouvez la vitesse et l'accélération pour les temps 0s, 0,5s et 1,0s. Dans chaque cas, indiquez si l'objet accélère ou décélère.
Répondre
La vitesse à chacun des instants indiqués est trouvée en substituant t directement dans l'équation. L'accélération est trouvée en dérivant l'expression donnée en fonction du temps, puis en évaluant le résultat à chacun des instants donnés.
Les résultats sont les suivants:
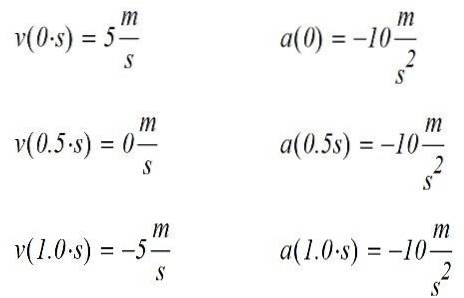
L'accélération est constante et négative pour tous les mouvements. Il est désormais possible de décrire ce qui est arrivé au mobile au fur et à mesure qu'il se déplace.
Au temps t = 0 s, le mobile ralentissait. Cela s'ensuit immédiatement puisque la vitesse est positive et l'accélération est négative..
A l'instant t = 0,5 s le mobile s'est arrêté, au moins momentanément il était au repos. Il n'est pas impossible pour un mobile de s'arrêter même lorsqu'il est accéléré. L'exemple le plus palpable est celui de la projection verticale.

Lorsqu'un mobile est projeté verticalement vers le haut, il parvient à atteindre une hauteur maximale. Si la direction positive est choisie dans ce sens, ce qui est presque toujours fait, pendant le temps qu'il faut pour atteindre ce point maximum, le mobile aura une vitesse positive.
Mais la gravité a duré tout le temps. Et il est toujours dirigé verticalement vers le bas, peu importe si l'objet monte ou descend. Naturellement, elle parvient à faire ralentir progressivement le mobile jusqu'à ce qu'il s'arrête un instant.
Immédiatement, le mobile renverse le sens de sa vitesse et retourne au sol. Dans ce cas, la vitesse est négative car elle pointe également vers le sol. Par conséquent, la gravité fait augmenter la vitesse de plus en plus.
La valeur de l'accélération de la pesanteur a été estimée à 9,8 m / sdeux, qui, à des fins de calcul, est arrondi à 10 m / sdeux. L'objet de l'exemple peut très bien avoir été projeté vers le haut avec une vitesse initiale de 5 m / s..
Enfin à t = 1,0 s, la vitesse du mobile est négative. S'il s'agit d'un jet vertical vers le haut, en l'absence de frottement, cela signifie qu'il passe à nouveau par le point de départ, mais cette fois il va vers le bas, au lieu de monter..
En conclusion, une accélération négative ne signifie pas forcément que le mobile ralentit. Au contraire, le mobile pourrait aller de plus en plus vite. Il s'agit de faire attention à savoir si les signes de vitesse et d'accélération sont identiques ou non..
Les références
- Walker, J. 2010. La physique. Quatrième édition. Addison Wesley. 26-30.



Personne n'a encore commenté ce post.