Formules de conductance, calculs, exemples, exercices

La conductance d'un conducteur est défini comme la facilité dont il dispose pour faire passer le courant électrique. Cela dépend non seulement du matériau utilisé pour sa fabrication, mais aussi de sa géométrie: longueur et section transversale.

Le symbole utilisé pour la conductance est G, et c'est l'inverse de la résistance électrique R, une quantité un peu plus familière. L'unité SI International System pour la conductance est l'inverse de l'ohm, noté Ω^-1 et reçoit le nom de siemens (S).

Les autres termes utilisés en électricité qui ressemblent à la conductance et qui sont liés sont conductivité et la conduite, mais ils ne doivent pas être confondus. Le premier de ces termes est une propriété intrinsèque de la substance avec laquelle le conducteur est fabriqué et le second décrit le flux de charge électrique à travers celui-ci..

Pour un conducteur électrique à section transversale constante À, longueur L et conductivité σ, la conductance est donnée par:

G = σ.A / L

Plus la conductivité est élevée, plus la conductance est élevée. De plus, plus la section transversale est grande, plus il est facile pour le conducteur de faire passer le courant. Au contraire, plus la longueur L est grande, plus la conductance est faible, car les porteurs de courant perdent plus d'énergie sur des trajets plus longs..

Index des articles

• 1 Comment la conductance est-elle calculée?
  • 1.1 Unités de conductance
• 2 exemples
  • 2.1 Conductivité et conductance
  • 2.2 Résistances en parallèle
• 3 exercices
  • 3.1 - Exercice 1
  • 3.2 - Exercice 2
• 4 Références

Comment la conductance est-elle calculée?

La conductance G pour un conducteur à section transversale constante est calculée selon l'équation donnée ci-dessus. Ceci est important, car si la section transversale n'est pas constante, vous devez utiliser le calcul intégral pour trouver à la fois la résistance et la conductance.

Puisqu'il s'agit de l'inverse de la résistance, la conductance G peut être calculée sachant que:

G = 1 / R

En fait, la résistance électrique d'un conducteur peut être mesurée directement avec un multimètre, un appareil qui mesure également le courant et la tension..

Unités de conductance

Comme indiqué au début, l'unité de conductance dans le système international est le Siemens (S). On dit qu'un conducteur a une conductance de 1 S si le courant qui le traverse augmente de 1 ampère pour chaque volt de différence de potentiel.

Voyons comment cela est possible grâce à la loi d'Ohm, si elle est écrite en termes de conductance:

V = I.R = I / G

Où V est la différence de tension ou de potentiel entre les extrémités du conducteur e je intensité du courant. En termes de ces grandeurs, la formule ressemble à ceci:

G = I / V

Auparavant, l'unité de conductance était le mho (ohm écrit à l'envers) noté Ʊ, qui est un oméga majuscule inversé. Cette notation a été déconseillée et a été remplacée par la siemens en l'honneur de l'ingénieur et inventeur allemand Ernst Von Siemens (1816-1892), pionnier des télécommunications, mais les deux sont totalement équivalents.

1 mho = 1 siemens = 1 A / V (ampère / volt)

Dans d'autres systèmes de mesure, le statsiemens (statS) (dans le système cgs ou centimètre-gramme-seconde) et le absiemens (abS) (système cgs électromagnétique) avec le "s" à la fin, sans indiquer le singulier ou le pluriel, car ils proviennent d'un nom propre.

Quelques équivalences

1 état = 1.11265 x 10 ^-12 siemens

1 abS = 1 x 10⁹ siemens

Exemples

Comme mentionné précédemment, ayant la résistance, la conductance est immédiatement connue lors de la détermination de la valeur inverse ou réciproque. De cette manière, une résistance électrique de 100 ohms équivaut à 0,01 siemens, par exemple.

Voici deux autres exemples d'utilisation de la conductance:

Conductivité et conductance

Ce sont des termes différents, comme déjà indiqué. La conductivité est une propriété de la substance avec laquelle le conducteur est fabriqué, tandis que la conductance est propre au conducteur.

La conductivité peut être exprimée en termes de G comme:

σ = G. (L / A)

Voici un tableau avec les conductivités des matériaux conducteurs fréquemment utilisés:

Tableau 1. Conductivités, résistivités et coefficient thermique de certains conducteurs. Température de référence: 20 ºC.

Métal	σ x 106 (Vous)	ρ x 10-8 (Ω.m)	α ºC-1
Argent	62,9	1,59	0,0058
Cuivre	56,5	1,77	0,0038
Or	41,0	2,44	0,0034
Aluminium	35,4	2,82	0,0039
Tungstène	18,0	5,60	0,0045
Fer	10,0	10,0	0,0050

Résistances en parallèle

Lorsque vous avez des circuits avec des résistances en parallèle, il est parfois nécessaire d'obtenir la résistance équivalente. Connaître la valeur de la résistance équivalente permet de substituer une valeur unique à l'ensemble des résistances.

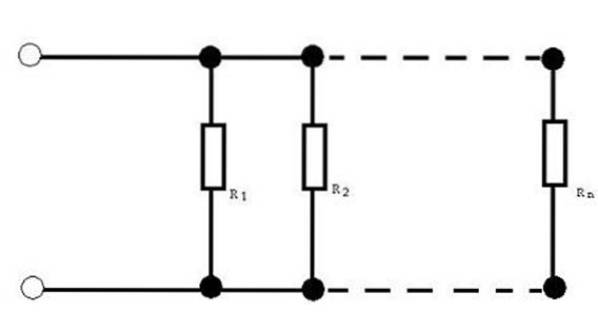
Pour cette configuration de résistance, la résistance équivalente est donnée par:

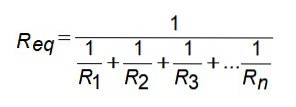
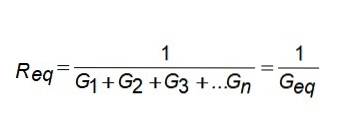
g_eq = G₁ + g_deux + g₃ +… G_n

Autrement dit, la conductance équivalente est la somme des conductances. Si vous voulez connaître la résistance équivalente, inversez simplement le résultat.

Exercices

- Exercice 1

a) Ecrire la loi d'Ohm en termes de conductance.

b) Trouvez la conductance d'un fil de tungstène de 5,4 cm de long et 0,15 mm de diamètre.

c) Maintenant, un courant de 1,5 A passe à travers le fil. Quelle est la différence de potentiel entre les extrémités de ce conducteur?

Solution pour

À partir des sections précédentes, vous devez:

V = I / G

G = σ.A / L

En remplaçant ce dernier dans le premier, cela ressemble à ceci:

V = I /(σ.A/L) = I.L / σ.A

Où:

-I est l'intensité du courant.

-L est la longueur du conducteur.

-σ est la conductivité.

-A est l'aire de la section transversale.

Solution b

Pour calculer la conductance de ce fil de tungstène, sa conductivité est nécessaire, qui se trouve dans le tableau 1:

σ = 18 x10⁶ vous

L = 5,4 cm = 5,4 x 10^-deux m

D = 0,15 mm = 0,15 x 10^-3 m

A = π.D^deux / 4 = π. (0,15 x 10^-3 m)^deux / 4 = 1,77 x 10^-8 m^deux

En substituant dans l'équation, nous avons:

G = σ.A / L = 18 x 10⁶ Vous . 1,77 x 10^-8 m^deux / 0,15 x 10^-3 m = 2120,6 S.

Solution c

V = I / G = 1,5 A / 2120,6 S = 0,71 mV.

- Exercice 2

Trouvez la résistance équivalente dans le circuit suivant et sachant que je_{ou alors} = 2 A, calculez i_X et la puissance dissipée par le circuit:

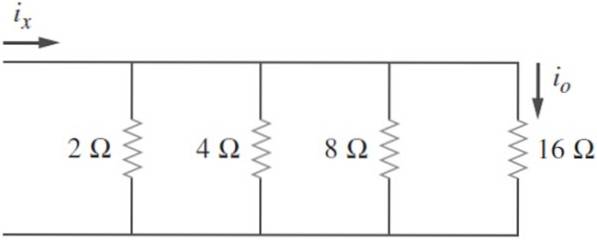
Solution

Les résistances sont répertoriées: R₁= 2 Ω; R_deux= 4 Ω; R₃= 8 Ω; R₄= 16 Ω

Ensuite, la conductance est calculée dans chaque cas: G₁ = 0,5 Ʊ; g_deux = 0,25 Ʊ; g₃ = 0,125 Ʊ; g₄ = 0,0625 Ʊ

Et enfin ils sont ajoutés comme indiqué précédemment, pour trouver la conductance équivalente:

g_eq = G₁ + g_deux + g₃ +… G_n = 0,5 Ʊ + 0,25 Ʊ + 0,125 Ʊ + 0,0625 Ʊ = 0,9375 Ʊ

Par conséquent R_eq = 1,07 Ω.

La tension aux bornes de R₄ c'est v₄ = i_{ou alors}. R₄ = 2 A. 16 Ω = 32 V, et il en va de même pour toutes les résistances, puisqu'elles sont connectées en parallèle. Ensuite, il est possible de trouver les courants qui traversent chaque résistance:

-je₁ = V₁ / R₁ = 32 V / 2 Ω = 16 A

-je_deux = V_deux / R_deux = 32 V / 4 Ω = 8 A

-je₃ = V₃ / R₃ = 32 V / 8 Ω = 4 A

-je_X = i₁ +  je_deux +  je₃ + je_{ou alors} = 16 + 8 + 4 + 2 A = 30 A

Enfin, la puissance dissipée P est:

P = (je_X)^deux. R_eq = 30 A x 1,07 Ω = 32,1 W

Les références

1. Alexander, C. 2006. Principes de base des circuits électriques. 3e. Édition. Mcgraw Hill.
2. Conversion mégaampère / millivolt en calculatrice absiemens. Récupéré de: pinkbird.org.
3. García, L. 2014. Electromagnétisme. 2ème. Édition. Université industrielle de Santander. La Colombie.
4. Knight, R. 2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique. Pearson.
5. Roller, D. 1990. Physique. Électricité, magnétisme et optique. Volume II. Éditorial Reverté.
6. Wikipédia. Conductance électrique. Récupéré de: es.wikipedia.org.
7. Wikipédia. Siemens. Récupéré de: es.wikipedia.org.