
Propriétés des ensembles finis, exemples, exercices résolus
Il est compris par ensemble fini tout ensemble avec un nombre limité ou dénombrable d'éléments. Des exemples d'ensembles finis sont les billes contenues dans un sac, l'ensemble des maisons d'un quartier ou l'ensemble P formé par les vingt (20) premiers nombres naturels:
P = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
L'ensemble des étoiles dans l'univers est certainement immense, mais on ne sait pas avec certitude s'il est fini ou infini. Cependant, l'ensemble des planètes du système solaire est fini.
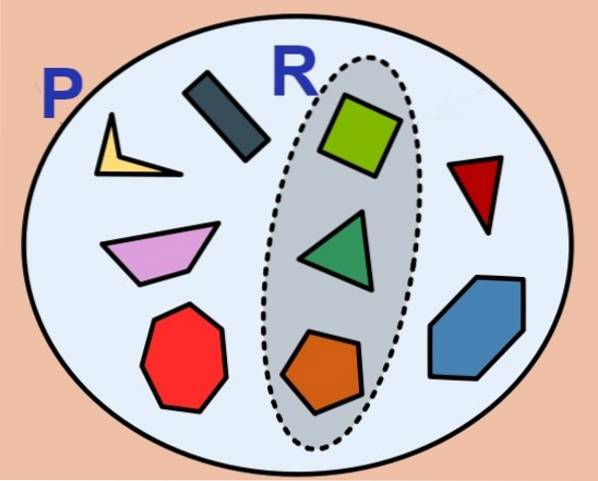
Le nombre d'éléments d'un ensemble fini est appelé sa cardinalité et pour l'ensemble P est noté comme ceci: Card (P) ou alors #P. L'ensemble vide a une cardinalité nulle et est considéré comme un ensemble fini.
Index des articles
- 1 Propriétés
- 2 exemples
- 2.1 Plus d'exemples
- 3 exercices résolus
- 3.1 Exercice 1
- 3.2 Exercice 2
- 3.3 Exercice 3
- 3.4 Exercice 4
- 4 Références
Propriétés
Parmi les propriétés des ensembles finis, on trouve les suivantes:
1- L'union d'ensembles finis donne naissance à un nouvel ensemble fini.
2- Si deux ensembles finis se croisent, il en résulte un nouvel ensemble fini.
3- Un sous-ensemble d'un ensemble fini est fini et sa cardinalité est inférieure ou égale à celle de l'ensemble d'origine.
4- L'ensemble vide est un ensemble fini.
Exemples
Il existe de nombreux exemples d'ensembles finis. Voici quelques exemples:
Ensemble M des mois de l'année, qui sous forme étendue peut s'écrire comme ceci:
M = Janvier, février, mars, avril, mai, juin, juillet, août, septembre, octobre, novembre, décembre, la cardinalité de M est 12.
Ensemble S des jours de la semaine: S = Lundi, mardi, mercredi, jeudi, vendredi, samedi, dimanche. La cardinalité de S est 7.
Ensemble Ñ des lettres de l'alphabet espagnol est un ensemble fini, cet ensemble par extension s'écrit comme ceci:
Ñ = a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z et sa cardinalité est 27.
Ensemble V des voyelles en espagnol est un sous-ensemble de l'ensemble Ñ:
V ⊂ Ñ c'est donc un ensemble fini.
L'ensemble fini V sous une forme extensive, il est écrit comme ceci: V = a, e, i, o, u et sa cardinalité est 5.
Les ensembles peuvent être exprimés par la compréhension. Ensemble F composé des lettres du mot «fini» est un exemple:
F = x / x est une lettre du mot "fini"
Ledit ensemble exprimé de manière extensive sera:
F = f, i, n, t, o dont la cardinalité est 5 et donc est un ensemble fini.
Plus d'exemples
Les couleurs de l'arc-en-ciel sont un autre exemple d'un ensemble fini, l'ensemble C de ces couleurs est:
C = rouge, orange, jaune, vert, cyan, bleu, violet et sa cardinalité est 7.
L'ensemble des phases F de la Luna est un autre exemple d'ensemble fini:
F = Nouvelle lune, premier quartier, pleine lune, dernier quartier cet ensemble a la cardinalité 4.
Un autre ensemble fini est celui formé par les planètes du système solaire:
P = Mercure, Vénus, Terre, Mars, Jupiter, Saturne, Uranus, Neptune, Pluton de cardinalité 9.
Exercices résolus
Exercice 1
L'ensemble suivant A = x∊ R / x ^ 3 = 27 est donné. Exprimez-le en mots et écrivez-le par extension, indiquez sa cardinalité et dites s'il est fini ou non.
Solution: L'ensemble A est l'ensemble des nombres réels x tels que x au cube de par conséquent 27.
L'équation x ^ 3 = 27 a trois solutions: ce sont x1 = 3, x2 = (-3/2 + 3√3 / 2 i) et x3 = (-3/2 - 3√3 / 2 i). Des trois solutions, seul x1 est réel, tandis que les deux autres sont des nombres complexes.
Puisque la définition de l'ensemble A dit que x appartient aux nombres réels, alors les solutions dans les nombres complexes ne font pas partie de l'ensemble A.
L'ensemble A exprimé de manière extensive est:
A = 3, qui est un ensemble fini de cardinalité 1.
Exercice 2
Écrivez sous forme symbolique (par compréhension) et sous forme extensive l'ensemble B des nombres réels supérieurs à 0 (zéro) et inférieurs ou égaux à 0 (zéro). Indiquez sa cardinalité et si elle est finie ou non.
Solution: B = x∊ R / 0 < x <= 0
L'ensemble B est vide car un nombre réel x ne peut pas être simultanément supérieur et inférieur à zéro, tout comme il ne peut pas être 0 et également inférieur à 0.
B = et sa cardinalité est 0. L'ensemble vide est un ensemble fini.
Exercice 3
L'ensemble S des solutions d'une certaine équation est donné. L'ensemble S par compréhension s'écrit comme ceci:
S = x∊ R / (x-3) (x ^ 2 - 9x + 20) = 0
Ecrire ledit ensemble sous une forme étendue, indiquer sa cardinalité et indiquer s'il s'agit ou non d'un ensemble fini.
Solution: En premier lieu, lors de l'analyse de l'expression qui décrit l'ensemble S, on obtient qu'il s'agit d'un ensemble de valeurs x réelles qui sont des solutions de l'équation:
(x-3) (x ^ 2 - 9x + 20) = 0 (*)
Une solution de cette équation est x = 3, qui est un nombre réel et appartient donc à S.Mais il y a plus de solutions qui peuvent être obtenues en recherchant les solutions de l'équation quadratique:
(x ^ 2 - 9x + 20) = 0
L'expression ci-dessus peut être factorisée comme suit:
(x - 4) (x - 5) = 0
Ce qui nous conduit à deux autres solutions de l'équation d'origine (*) qui sont x = 4 et x = 5. En bref, l'équation (*) a pour solutions 3, 4 et 5.
L'ensemble S exprimé sous forme extensive ressemble à ceci:
S = 3, 4, 5, qui a la cardinalité 3 et est donc un ensemble fini.
Exercice 4
Il y a deux ensembles A = 1, 5, 7, 9, 11 et B = x ∊ N / x est pair ^ x < 10 .
Écrivez explicitement l'ensemble B et trouvez l'union avec l'ensemble A. Trouvez également l'intersection de ces deux ensembles et concluez.
Solution: l'ensemble B est composé d'entiers naturels tels qu'ils sont pairs et sont également inférieurs à la valeur 10, donc dans l'ensemble B sous forme extensive, il s'écrit comme suit:
B = 2, 4, 6, 8
L'union de l'ensemble A avec l'ensemble B est:
A U B = 1, 2, 4, 5, 6, 7, 8, 9, 11
et l'interception de l'ensemble A avec l'ensemble B s'écrit comme ceci:
A ⋂ B = = Ø est l'ensemble vide.
Il convient de noter que l'union et l'interception de ces deux ensembles finis conduisent à de nouveaux ensembles, qui à leur tour sont également finis.
Les références
- Fuentes, A. (2016). MATHÉMATIQUES DE BASE. Une introduction au calcul. Lulu.com.
- Garo, M. (2014). Mathématiques: équations quadratiques: comment résoudre une équation quadratique. Marilù Garo.
- Haeussler, E. F. et Paul, R. S. (2003). Mathématiques pour la gestion et l'économie. Éducation Pearson.
- Jiménez, J., Rodríguez, M., Estrada, R. (2005). Mathématiques 1 SEP. Au seuil.
- Preciado, C. T. (2005). Cours de mathématiques 3e. Progreso éditorial.
- Mathématiques 10 (2018). "Exemples d'ensembles finis". Récupéré de: matematicas10.net
- Rock, N. M. (2006). L'algèbre I est facile! Si facile. Team Rock Press.
- Sullivan, J. (2006). Algèbre et trigonométrie. Éducation Pearson.
- Wikipédia. Ensemble fini. Récupéré de: es.wikipedia.com



Personne n'a encore commenté ce post.