
Exemples de coordonnées rectangulaires et exercices résolus
le Coordonnées rectangulaires ou cartésiens sont ceux que l'on obtient en projetant orthogonalement sur les trois axes cartésiens X, Y, Z un point situé dans l'espace tridimensionnel.
Les axes cartésiens sont des lignes orientées mutuellement perpendiculaires les unes aux autres. Dans le système de coordonnées cartésien, chaque point de l'espace se voit attribuer trois nombres réels qui sont ses coordonnées rectangulaires.
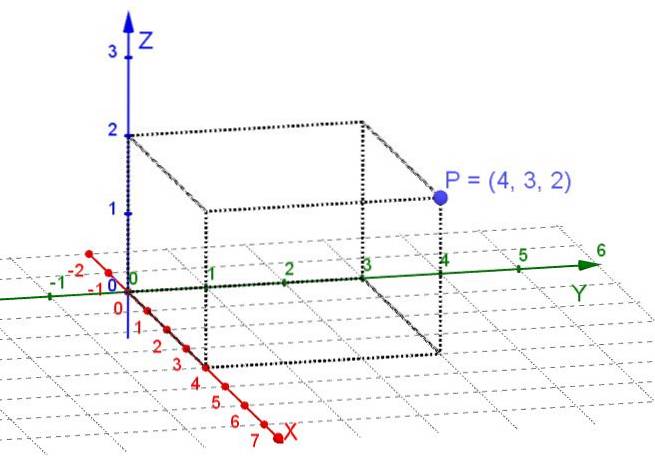
Un plan est un sous-espace d'un espace tridimensionnel. En cas de considération de points sur un plan, il suffit alors de choisir une paire d'axes perpendiculaires X, Y comme système cartésien. Ensuite, chaque point du plan se voit attribuer deux nombres réels qui sont ses coordonnées rectangulaires.
Index des articles
- 1 Origine des coordonnées rectangulaires
- 2 Le plan cartésien
- 2.1 Distance entre deux points
- 2.2 Expression analytique d'une ligne
- 3 exemples
- 3.1 Exemple 1
- 3.2 Exemple 2
- 4 exercices résolus
- 4.1 Exercice 1
- 4.2 Exercice 2
- 5 Références
Origine des coordonnées rectangulaires
Les coordonnées rectangulaires ont été proposées à l'origine par le mathématicien français René Descartes (1596 et 1650), c'est pourquoi elles sont appelées cartésiennes.
Avec cette idée de Descartes, les points du plan et de l'espace sont numérotés, de sorte que les figures géométriques ont une équation algébrique associée et les théorèmes géométriques classiques peuvent être prouvés algébriquement. Avec les coordonnées cartésiennes, la géométrie analytique est née.
Le plan cartésien
Si dans un plan on choisit deux droites perpendiculaires qui se coupent en un point O; et si, en plus, chaque ligne se voit attribuer une direction et une échelle numérique entre des points équidistants successifs, alors il y a un système ou plan cartésien dans lequel chaque point du plan est associé à une paire ordonnée de deux nombres réels qui sont leurs projections respectivement sur les axes X et Y.
Les points A = (3, 2); B = (- 2, 3); C = (- 2, -3) et D = (3, -3) sont représentés dans le plan cartésien comme indiqué ci-dessous:
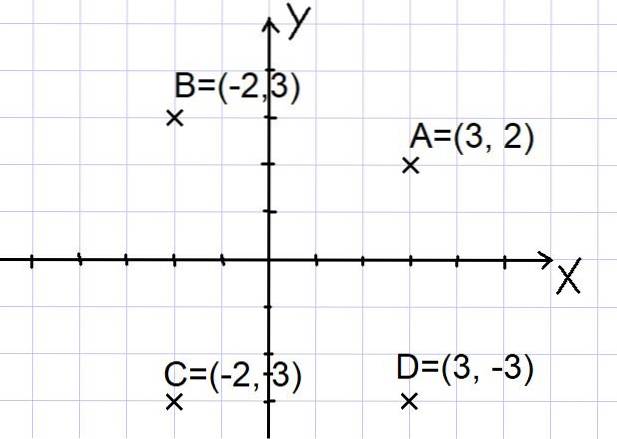
Notez que les deux axes X et Y divisent le plan en quatre secteurs appelés quadrants. Le point A est dans le premier quadrant, B est dans le deuxième quadrant, C est dans le troisième quadrant et le point D est dans le quatrième quadrant..
Distance entre deux points
La distance entre deux points A et B sur le plan cartésien est la longueur du segment qui les relie. Cette distance peut être calculée analytiquement comme suit:
d (A, B) = √ (Bx - Axe) ^ 2 + (Par - Ay) ^ 2)
La formule ci-dessus est obtenue en appliquant le théorème de Pythagore.
En appliquant cette formule aux points A, B de la figure 2, nous avons:
d (A, B) = √ (-2 - 3) ^ 2 + (3 - 2) ^ 2) = √ (-5) ^ 2 + 1 ^ 2) = √ (26)
Autrement dit, d (A, B) = 5,10 unités. Notez que la distance a été obtenue sans qu'il soit nécessaire de mesurer avec une règle, une procédure complètement algébrique a été suivie.
Expression analytique d'une ligne
Les coordonnées rectangulaires permettent la représentation analytique des objets géométriques fondamentaux tels que le point et la ligne. Deux points A et B définissent une seule ligne. La pente de la droite est définie comme le quotient entre la différence des coordonnées Y du point B moins A, divisée par la différence des coordonnées X du point B moins A:
pente = (By - Ay) / (Bx - Ax)
Tout point P de coordonnées (x, y) appartenant à la droite (AB) doit avoir la même pente:
pente = (y - Ay) / (x - Ax)
L'équation obtenue au moyen de l'égalité des pentes est la représentation analytique ou algébrique de la droite passant par les points A et B:
(y - Ay) / (x - Ax) = (Par - Ay) / (Bx - Ax).
Si nous prenons pour A et B les coordonnées rectangulaires de la figure 2, nous avons:
(y - 2) / (x - 3) = (3 - 2) / (- 2 - 3)
(y - 2) / (x - 3) = -⅕
Dans ce cas particulier, nous avons une ligne avec une pente négative -⅕, ce qui signifie qu'en localisant sur un point de la ligne et en augmentant la coordonnée x d'une unité, la coordonnée y diminue de 0,2 unité.
La manière la plus courante d'écrire l'équation de la ligne dans le plan consiste à effacer la coordonnée y en fonction de la variable x:
y = - (1/5) x + 13/5
Exemples
Exemple 1
Obtenir par des méthodes analytiques la distance entre les points C et A, étant les coordonnées rectangulaires de C = (-2, -3) et celles de A = (3,2).
La formule de la distance euclidienne entre ces deux points s'écrit comme ceci:
d (A, C) = √ ((Cx - Ax) ^ 2 + (Cy - Ay) ^ 2)
En substituant leurs coordonnées rectangulaires correspondantes, nous avons:
d (A, C) = √ (-2 - 3) ^ 2 + (-3 - 2) ^ 2) = √ (-5) ^ 2 + (-5) ^ 2) = 5√2 = 7,07
Exemple 2
Obtenir l'équation de la droite passant par le point C de coordonnées (-2, -3) et le point P de coordonnées (2, 0).
Tout d'abord, la pente de la droite CP est obtenue:
pente = (0 - (- 3)) / (2 - (-2)) = ¾
Tout point Q de coordonnées rectangulaires génériques (x, y) appartenant à la ligne CP doit avoir la même pente:
pente = (y - (- 3)) / (x - (-2)) = (y +3) / (x +2)
En d'autres termes, l'équation de la droite CP est:
(y +3) / (x +2) = ¾
Une autre manière d'écrire l'équation de la droite CP consiste à résoudre pour y:
y = ¾ x - 3/2
Exercices résolus
Exercice 1
Obtenir les coordonnées rectangulaires du point d'intersection entre les lignes y = - (1/5) x + 13/5 et la ligne y = ¾ x - 3/2.
Solution: Par définition, le point d'intersection des deux lignes partage les mêmes coordonnées rectangulaires. Par conséquent, les coordonnées y au point d'intersection sont identiques pour les deux lignes:
-(1/5) x + 13/5 = ¾ x - 3/2
ce qui conduit à l'expression suivante:
(¾ + ⅕) x = 13/5 +3/2
en résolvant la somme des fractions, nous obtenons:
19/20 x = 41/10
Résolution pour x:
x = 82/19 = 4,32
Pour obtenir l'ordonnée à l'origine, la valeur x obtenue est substituée dans l'une des lignes:
y = ¾ 4,32 - 3/2 = 1,74
Cela signifie que les droites données se croisent au point I de coordonnées I = (4.32, 1.74).
Exercice 2
Obtenir l'équation de la circonférence qui passe par le point R de coordonnées rectangulaires (3, 4) et qui a son centre à l'origine des coordonnées.
Solution: Le rayon R est la distance du point R à l'origine O des coordonnées (0, 0).
d (R, O) = √ ((Rx - 0) ^ 2 + (Ry - 0) ^ 2) = √ ((3 - 0) ^ 2 + (4 - 0) ^ 2) = √ (3 ^ 2 + 4 ^ 2) = √ (9 + 16) = √ (25) = 5
Autrement dit, c'est un cercle de rayon 5 centré en (0,0).
Tout point P (x, y) sur la circonférence doit avoir la même distance 5 du centre (0, 0) pour pouvoir s'écrire:
d (P, O) = √ ((x - 0) ^ 2 + (y - 0) ^ 2) = √ (x ^ 2 + y ^ 2) = 5
C'est-à-dire:
√ (x ^ 2 + y ^ 2) = 5
Pour éliminer la racine carrée, les deux membres de l'égalité sont au carré, obtenant:
x ^ 2 + y ^ 2 = 25
Quelle est l'équation de la circonférence.
Cet exemple illustre la puissance du système de coordonnées rectangulaires, qui permet de déterminer des objets géométriques, tels que la circonférence, sans avoir besoin d'utiliser du papier, un crayon et une boussole. La circonférence demandée a été déterminée uniquement par des méthodes algébriques.
Les références
- Arfken G et Weber H. (2012). Méthodes mathématiques pour les physiciens. Un guide complet. 7e édition. Presse académique. ISBN 978-0-12-384654-9
- Calcul cc. Résolution des problèmes de coordonnées rectangulaires. Récupéré de: calculo.cc
- Weisstein, Eric W. «Coordonnées cartésiennes». De MathWorld-A Wolfram Web. Récupéré de: mathworld.wolfram.com
- Wikipédia. Système de coordonnées cartésiennes. Récupéré de: en.wikipedia.com



Personne n'a encore commenté ce post.