
Diagramme corporel gratuit comment le faire, exemples, exercice
UNE Diagramme de corps libre, diagramme de corps isolé ou diagramme de force, est un diagramme où les forces agissant sur un corps sont représentées par des flèches.
Assurez-vous d'inclure dans le diagramme toutes les forces qui agissent sur l'objet, et puisqu'il s'agit d'une grandeur vectorielle, la flèche se charge d'indiquer sa direction et son sens, tandis que sa longueur donne une idée du module ou de l'intensité.
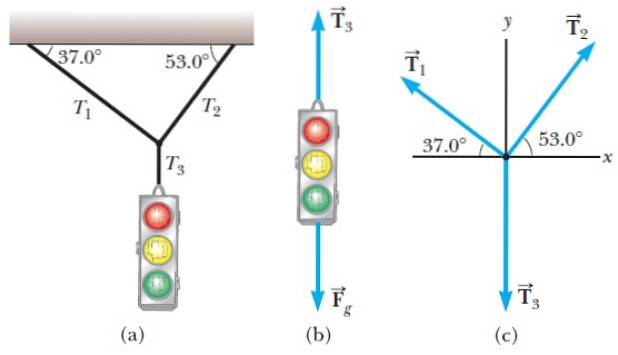
Dans la figure 1, nous avons un exemple de diagramme de corps libre que nous allons analyser.
La situation est la suivante: un feu tricolore suspendu au repos à certains câbles (figure 1a). Deux forces agissent sur elle, l'une est celle exercée par la Terre, qui est le poids. Dans le diagramme, il est noté Fg et agit verticalement vers le bas.
L'autre force est la tension dans la corde verticale, appelée T3 et qui va dans une direction verticale vers le haut, tenant le feu de signalisation et l'empêchant de tomber au sol.
Lorsqu'un problème a plus d'un objet, il est alors nécessaire de dessiner un diagramme pour chacun d'eux séparément..
Le nœud entre les cordes inclinées et la corde qui retient le feu de signalisation est considéré comme un objet ponctuel et son diagramme de corps libre est sur la figure 1c. Notez que pour le nœud, la tension T3 est dirigé vers le bas.
Il est important de noter que les forces exercées par l'objet sur d'autres corps ne doivent pas apparaître dans le diagramme du corps libre, mais seulement ceux qui agissent dessus.
Index des articles
- 1 Exemples de diagramme de corps libre
- 1.1 Une personne qui tire un coffre ou un conteneur
- 1.2 Un bloc glissant sur un plan incliné
- 1.3 La machine d'Atwood
- 2 Exercice résolu
- 2.1 Solution
- 3 Références
Exemples de diagramme de corps libre
Le diagramme du corps libre permet l'application des lois de Newton et détermine avec elles l'état de mouvement ou de repos de l'objet sur lequel les forces agissent. Dans le cas du feu tricolore représenté, on peut déterminer la valeur des tensions dans les câbles qui retiennent le feu tricolore, connaissant le poids de ce.
Une fois ces données connues, des câbles adaptés sont sélectionnés pour accrocher le feu et qui remplissent leur fonction sans s'effondrer.
Les diagrammes du corps libre sont utilisés pour décrire diverses situations quotidiennes, telles que celles-ci:
Une personne tirant un coffre ou un conteneur
Il est très courant que les gens doivent porter des objets lourds tels que le conteneur sur la figure. Pour ce faire, ils doivent exercer une force F à propos du conteneur, qui dans cet exemple est horizontal et à droite, qui est la direction du mouvement.
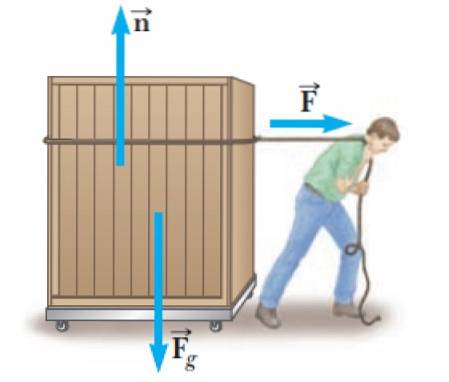
Mais ce n'est pas la seule force qui agit sur lui, il y a aussi le normal n, exercé par la surface plane de la plate-forme à roues. Et enfin il y a le poids de celui-ci: Fg, dirigé verticalement vers le bas.
La normale est une force qui survient chaque fois que deux surfaces sont en contact et est toujours perpendiculaire à la surface qui l'exerce. Dans ce cas, la plate-forme à roues exerce une normalité sur le conteneur.
Un bloc glissant sur un plan incliné
Certains bureaux ont la table légèrement inclinée pour faciliter la prise de notes et la lecture. Il a également une fente pour porte-crayon, mais nous avons tous mis le crayon sur la table hors de la fente et nous avons vu comment il glisse sur la table.
Quelles forces agissent sur le crayon?
Les mêmes qui agissent sur le bloc montré dans le diagramme de corps libre suivant:
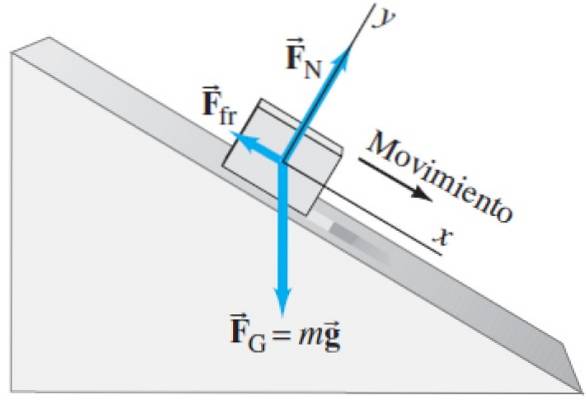
Le normal FN est la force que la surface de la table exerce sur le crayon ou le bloc supporté. Contrairement à l'exemple précédent, la normale n'est pas verticale, mais inclinée. Rappelez-vous que la normale est la force que la table exerce sur le bloc et est perpendiculaire à celui-ci. Comme la table est inclinée, la table normale aussi.
Comme toujours le poids Fg est vertical, quelle que soit l'inclinaison du système.
Et enfin nous avons une nouvelle force agissant, qui est le frottement cinétique Ffr entre la table et le crayon ou le bloc. Le frottement est également une force de contact, mais contrairement à la normale, il s'agit d'une force tangentielle (parallèle) à la surface. Notez également qu'il est toujours dirigé dans le sens opposé au mouvement..
La machine d'Atwood
La machine Atwood est une machine simple qui se compose d'une poulie légère et sans frottement sur le rail, à travers laquelle passe une corde légère et inextensible.
Deux objets de masse m y sont suspendus1 et Mdeux. Lorsqu'un des objets monte, l'autre descend, comme le montre la figure 4a:
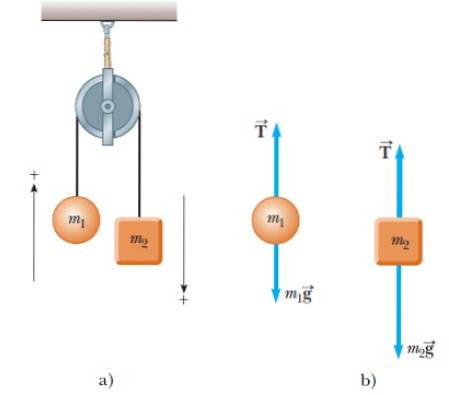
Puisqu'il y a deux objets, un diagramme de corps libre est fait pour chacun séparément. Pour les deux objets, il n'y a que deux forces: la tension dans la corde T et les poids respectifs.
Sur la figure, chaque poids est exprimé directement comme le produit de la masse et de l'accélération. De son côté, la tension est toujours dirigée verticalement le long de la corde tendue.
Exercice résolu
Appliquez les lois de Newton pour déterminer l'accélération avec laquelle les masses se déplacent de la machine Atwood montrée dans la section précédente.
Solution
La deuxième loi de Newton stipule que la somme des forces est égale au produit de la masse et de l'accélération.
La convention de signe dans chaque masse peut être différente, nous allons donc prendre le mouvement comme un sens positif, comme indiqué dans le graphique, la première masse augmente et la seconde diminue.
Dans certains problèmes, la déclaration ne fournit pas d'informations, alors les signes doivent être attribués arbitrairement et si le résultat de l'accélération est négatif, alors le système de masse se déplace dans la direction opposée à celle initialement supposée.
-Pour la masse 1 (monte):
T - m1g = m1à
-Pour la masse 2 (faible):
-T + mdeuxg = mdeuxà
Les deux équations forment un système d'équations linéaires de deux inconnues, comme la tension apparaît avec un signe différent dans chaque équation, nous les ajoutons simplement terme par terme et la tension s'annule:
mdeuxg - m1g = m1a + mdeuxà
a = mdeuxg - m1g / (m1 + mdeux)
Les références
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
- Giancoli, D. 2006. Physique: principes avec applications. 6e. Salle des Prentices Ed.
- Serway, R., Vulle, C. 2011. Physique universitaire. 9e éd. Cengage Learning.
- Tipler, P. (2006) Physique pour la science et la technologie. 5e éd. Volume 1. Éditorial Reverté.
- Tippens, P. 2011. Physique: concepts et applications. 7e édition. Mcgraw Hill



Personne n'a encore commenté ce post.