Différence de formules de cubes, équations, exemples, exercices

La différence de cubes est une expression algébrique binomiale de la forme a³ - b³, où les termes a et b peuvent être des nombres réels ou des expressions algébriques de différents types. Un exemple de différence de cubes est: 8 - x³, puisque 8 peut être écrit comme 2³.

Géométriquement, nous pouvons penser à un grand cube, avec le côté a, duquel le petit cube avec le côté b est soustrait, comme illustré sur la figure 1:

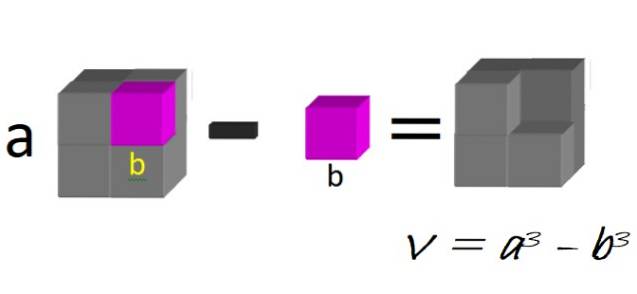
Le volume de la figure résultante est précisément une différence de cubes:

V = a³ - b³

Pour trouver une expression alternative, on observe que cette figure peut être décomposée en trois prismes, comme indiqué ci-dessous:

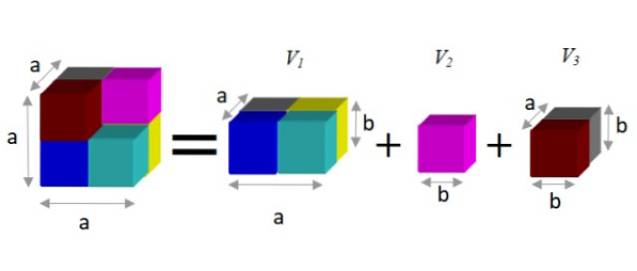
Un prisme a un volume donné par le produit de ses trois dimensions: largeur x hauteur x profondeur. De cette manière, le volume résultant est:

V = a³ - b³ = a^deux.b + b³ + un B^deux

Le facteur b il est commun à la droite. De plus, dans la figure ci-dessus, il est particulièrement vrai que:

b = (a / 2) ⇒ a = b + b

On peut donc dire que: b = a - b. De cette façon:

à³ - b³ = b (un^deux + b^deux +a.b) = (a-b) (a^deux + a.b + b^deux)

Cette façon d'exprimer la différence des cubes s'avérera très utile dans de nombreuses applications et aurait été obtenue de la même manière, même si le côté du cube manquant dans le coin était différent de b = a / 2.

Notez que la deuxième parenthèseressemble beaucoup au produit remarquable du carré de la somme, mais le terme croisé n'est pas multiplié par 2. Le lecteur peut développer le côté droit pour vérifier qu'il est effectivement obtenu à³ - b³.

Index des articles

• 1 Exemples
  • 1.1 Factorisation d'une différence de cubes
• 2 Exercice résolu
  • 2.1 Exercice 1
  • 2.2 Exercice 2
• 3 Références

Exemples

Il existe plusieurs différences de cubes:

1 - m⁶

à⁶b³ - 8z¹²Oui⁶

(1/125) .x⁶ - 27 et⁹

Analysons chacun d'eux. Dans le premier exemple, le 1 peut s'écrire 1 = 1³ et le terme m⁶ reste: (m^deux)³. Les deux termes sont des cubes parfaits, donc leur différence est:

1 - m⁶ = 1³ - (m^deux)³

Dans le deuxième exemple, les termes sont réécrits:

à⁶b³ = (un^deuxb)³

8z¹²Oui⁶ = 2³ (z⁴)³ (O^deux)³ = (2z⁴Oui^deux)³

La différence de ces cubes est: (a^deuxb)³ - (2z⁴Oui^deux)³.

Enfin, la fraction (1/125) est (1/5³), X⁶ = (x^deux)³, 27 = 3³ et et⁹ = (et³)³. En remplaçant tout cela dans l'expression originale, vous obtenez:

(1/125) .x⁶  - 27 ans⁹ = [(1/5) (x^deux)]³ - (3 ans³)³

Factoriser une différence de cubes

La factorisation de la différence des cubes simplifie de nombreuses opérations algébriques. Pour ce faire, il suffit d'utiliser la formule déduite ci-dessus:

Maintenant, la procédure pour appliquer cette formule se compose de trois étapes:

- Tout d'abord, la racine cubique de chacun des termes de la différence est obtenue.

- Ensuite, le binôme et le trinôme qui apparaissent sur le côté droit de la formule sont construits.

- Enfin le binôme et le trinôme sont substitués pour obtenir la factorisation définitive.

Illustrons l'utilisation de ces étapes avec chacun des exemples de différence de cube proposés ci-dessus et obtenons ainsi son équivalent pondéré.

Exemple 1

Factoriser l'expression 1 - m⁶   en suivant les étapes décrites. Nous commençons par réécrire l'expression comme 1 - m⁶ = 1³ - (m^deux)³ pour extraire les racines cubiques respectives de chaque terme:

Ensuite, le binôme et le trinôme sont construits:

a = 1

b = m^deux

Ensuite:

a - b = 1 - m^deux

 (à^deux +a.b + b^deux) = 1^deux + 1 m^deux + (m^deux)^deux = 1 + m^deux + m⁴

 Enfin, il est remplacé dans la formule a³ - b³ = (a-b) (a^deux +a.b + b^deux):

1 - m⁶ = (1 - m^deux) (1 + m^deux + m⁴)

Exemple 2

Factoriser:

à⁶b³ -8z¹²Oui⁶ = (un^deuxb)³ - (2z⁴Oui^deux)³

Comme ce sont des cubes parfaits, les racines cubiques sont immédiates: a^deuxb et 2z⁴Oui^deux, il s'ensuit donc que:

- Binomial: a^deuxb - 2z⁴Oui^deux

- Trinomial: (un^deuxb)^deux + à^deuxb. 2z⁴Oui^deux + (à^deuxb + 2z⁴Oui^deux)^deux

 Et maintenant, la factorisation souhaitée est construite:

à⁶b³ -8z¹²Oui⁶ = (un^deuxb - 2z⁴Oui^deux). [(à^deuxb)^deux + à^deuxb. 2z⁴Oui^deux + (à^deuxb + 2z⁴Oui^deux)^deux] =

= (un^deuxb - 2z⁴Oui^deux). [à⁴b^deux + 2e^deuxb.z⁴Oui^deux + (à^deuxb + 2z⁴Oui^deux)^deux]

En principe, l'affacturage est prêt, mais il est souvent nécessaire de simplifier chaque terme. Ensuite, nous développons le produit remarquable - carré d'une somme - qui apparaît à la fin et ajoutons des termes similaires. En se rappelant que le carré d'une somme est:

(x + y)^deux = x^deux + 2xy + et^deux

Le produit notable à droite est développé comme ceci:

(à^deuxb + 2z⁴Oui^deux)^deux = a⁴b^deux + 4e^deuxb.z⁴Oui^deux + 4z⁸Oui⁴

 En substituant l'expansion obtenue dans la factorisation de la différence des cubes:

à⁶b³ -8z¹²Oui⁶ = (un^deuxb - 2z⁴Oui^deux). [à⁴b^deux + 2e^deuxb.z⁴Oui^deux + à⁴b^deux + 4e^deuxb.z⁴Oui^deux + 4z⁸Oui⁴] =

Enfin, en regroupant des termes semblables et en factorisant les coefficients numériques, qui sont tous égaux, on obtient:

(à^deuxb - 2z⁴Oui^deux). [2a⁴b^deux + 6e^deuxb.z⁴Oui^deux + 4z⁸Oui⁴] = 2 (un^deuxb - 2z⁴Oui^deux). [à⁴b^deux + 3e^deuxb.z⁴Oui^deux + 2z⁸Oui⁴]

Exemple 3

Facteur (1/125) .x⁶  - 27 ans⁹ c'est beaucoup plus simple que le cas précédent. Tout d'abord, les équivalents de a et b sont identifiés:

a = (1/5) x^deux

b = 3y³

Ensuite, ils sont directement substitués dans la formule:

(1/125) .x⁶  - 27 ans⁹ = [(1/5) x^deux - 3 ans³]. [(1/25) x⁴ + (3/5) x^deuxOui³ + 9 ans⁶]

Exercice résolu

La différence des cubes a, comme nous l'avons dit, une variété d'applications en Algèbre. Voyons quelques-uns:

Exercice 1

Résolvez les équations suivantes:

a) x⁵ - 125 x^deux = 0

b) 64 à 729 x³ = 0

Solution pour

Tout d'abord, l'équation est prise en compte de cette manière:

X^deux (X³ - 125) = 0

Puisque 125 est un cube parfait, les parenthèses sont écrites comme une différence de cubes:

X^deux . (X³ - 5³) = 0

La première solution est x = 0, mais on en trouve plus si on fait x³ - 5³ = 0, alors:

X³ = 5³ → x = 5

Solution b

Le côté gauche de l'équation est réécrit comme 64 - 729 x³ = 4³ - (9x)³. Donc:

4³ - (9x)³ = 0

Puisque l'exposant est le même:

9x = 4 → x = 9/4

Exercice 2

Factorisez l'expression:

(x + y)³ - (x - y)³

Solution

Cette expression est une différence de cubes, si dans la formule de factorisation on note que:

a = x + y

b = x- y

Ensuite, le binôme est construit en premier:

a - b = x + y - (x- y) = 2y

Et maintenant le trinôme:

à^deux + a.b + b^deux = (x + y)^deux + (x + y) (x-y) + (x-y)^deux

Des produits notables sont développés:

(x + y)^deux = x^deux + 2xy + et^deux

(x + y) (x-y) = x^deux- Oui^deux

(x- y)^deux = x^deux - 2xy + et^deux

Ensuite, vous devez remplacer et réduire des termes similaires:

à^deux + a.b + b^deux = x^deux + 2xy + et^deux+ X^deux- Oui^deux+ X^deux - 2xy + et^deux = 3x^deux + Oui^deux

L'affacturage se traduit par:

(x + y)³ - (x - y)³ = 2y. (3x^deux + Oui^deux)

Les références

1. Baldor, A. 1974. Algèbre. Éditorial Cultural Venezolana S.A.
2. Fondation CK-12. Somme et différence de cubes. Récupéré de: ck12.org.
3. Khan Academy. Factorisation des différences de cubes. Récupéré de: es.khanacademy.org.
4. Les mathématiques sont amusantes avancées. Différence de deux cubes. Récupéré de: mathsisfun.com
5. UNAM. Factoriser une différence de cubes. Récupéré de: dcb.fi-c.unam.mx.