le différences entre la population et l'échantillon en statistique, ils découlent du fait que la population est l'univers des éléments à étudier, alors que l'échantillon est une partie représentative de la population.
Analyser un échantillon pris dans son ensemble, au lieu de l'ensemble, représente un net avantage en termes de gestion de l'information. Voyons plus en détail les principales différences entre les deux concepts ci-dessous..
Il est clair maintenant qu'une population peut être constituée d'un très grand ensemble d'éléments: des personnes, des animaux, des micro-organismes ou des particules. Aborder l'étude de chacun de ces éléments séparément consomme une grande quantité de ressources, de temps et d'efforts..
Mais en choisissant un échantillon soigneusement sélectionné, les résultats issus de son étude sont étendus à la population, sans perte significative d'informations..
| Ville | Spectacle | |
| Définition | L'ensemble de tous les éléments considérés pour une étude. | Il fait partie de la population, sélectionné pour être représentatif et ainsi faciliter son analyse. |
| symbole | Taille de la population: N | Taille de l'échantillon: n |
| Analyse | A des paramètres, tels que des valeurs descriptives. | Il est analysé à l'aide de statistiques. |
| Exemples | Nombre total d'oiseaux qui habitent une forêt. | Pour une enquête, 1000 oiseaux sont prélevés dans une forêt. |
En statistique, le concept de population a un sens plus large que celui de tous les jours. Une population est associée au nombre d'habitants d'un pays ou d'une ville, cependant une population statistique peut être constituée de personnes et d'êtres vivants, mais aussi d'objets grands et petits, de particules, d'événements, d'événements et d'idées..
Des exemples de populations de nature diverse sont:
-Molécules d'air à l'intérieur d'un contenant scellé.
-Toutes les étoiles de la Voie lactée.
-Les oiseaux qui peuplent une forêt.
-Le nombre total d'arbres dans cette même forêt ou dans une autre.
-L'ensemble des abonnés d'une compagnie de téléphone qui a des succursales en Amérique et en Europe.
-Les lancers que nous faisons d'une pièce.
-Le nombre de bactéries dans une culture.
-La production mensuelle de vis dans une usine.
Nous savons déjà à quel point les populations peuvent être diversifiées. Voyons maintenant comment ils peuvent être classés en fonction de leur extension.
Une quantité finie est celle qui peut être exprimée par un nombre, tel que le nombre de billes dans une boîte. Par contre, d'une quantité infinie on ne peut pas donner une valeur précise.
Cette différence nous permettra de définir deux types de populations en fonction de leur extension.
Supposons que vous ayez 20 billes dans une boîte et que vous échantillonniez 2 billes sans les remplacer. Finalement, les billes dans la boîte seront épuisées, donc la population est finie.
Un nombre peut être fini même s'il est très grand. Une culture de bactéries est constituée d'un grand nombre, mais elle est finie, comme le nombre d'étoiles dans la galaxie ou les molécules d'une portion de gaz enfermée dans un récipient..
Que se passe-t-il si chaque fois que nous extrayons un échantillon de billes, nous les remettons dans la boîte après les avoir observées? Dans ce cas on peut prélever un nombre infini d'échantillons, et ainsi considérer que la population de billes est infinie.
Nous avons un autre exemple d'une population infinie dans le tirage au sort de pièces ou de dés, car en théorie, vous pouvez prélever tous les échantillons que vous voulez, sans aucune limite..
Même une population finie connue pour contenir un grand nombre d'éléments peut être considérée comme infinie en pratique, si nécessaire..
Pour cette raison, il est très important de bien définir la population avant d'entreprendre l'étude, ce qui signifie fixer ses limites, car sa taille déterminera la forme et la taille des échantillons qui en seront tirés ultérieurement..
Il est également important de connaître la localisation chronologique de la population. Ce n'est pas la même chose d'étudier les registres des habitants d'une grande ville au début du XXe siècle que de faire de même avec les habitants d'une même ville au début du XXIe siècle..
De même, l'analyste doit veiller à prendre en compte la localisation de la population, ainsi qu'à vérifier son homogénéité - ou son absence.-.
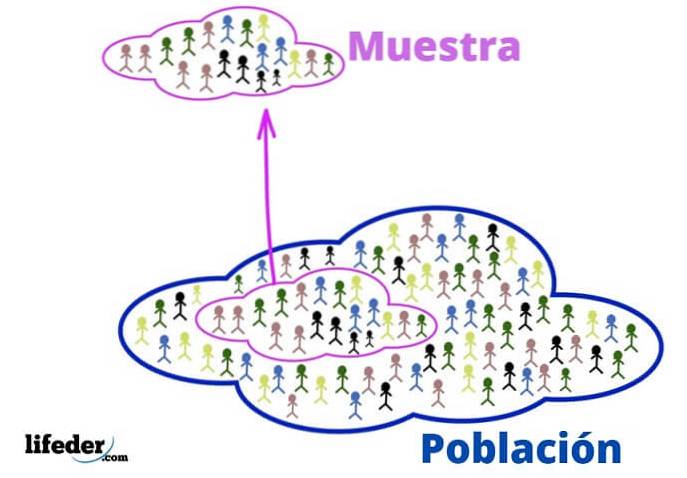
L'échantillon est l'ensemble des éléments sélectionnés dans la population pour le représenter. Le but de le faire, comme nous l'avons dit, est de rendre le travail plus facile. En traitant moins de données, moins de ressources sont investies et des résultats plus rapides sont obtenus.
Cependant, pour qu'il fonctionne correctement, l'échantillon doit être adéquat. Le processus de sélection est effectué à l'aide de techniques d'échantillonnage utilisant des critères mathématiques..
L'échantillon tiré n'a pas à être unique. En fait, une population peut donner lieu à plusieurs échantillons.
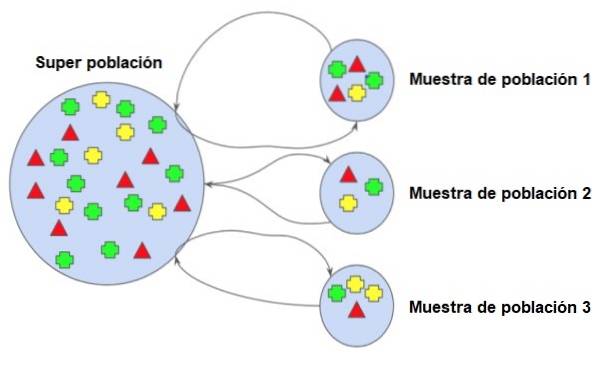
Par exemple, supposons que la population est l'ensemble des élèves d'une école secondaire qui a plusieurs sections pour chaque année. Un échantillon représentatif doit contenir des élèves de chacune des sections de chaque année, par exemple ceux dont le nom commence par la lettre A.
D'un autre côté, un échantillon moins représentatif pourrait l'être si tous les élèves de la même année étaient choisis. Regardons quelques exemples supplémentaires:
Les propriétaires de grands magasins veulent estimer le montant moyen que les clients dépensent pour faire leurs courses. Pour ce faire, ils collectent toutes les factures pendant une certaine période, disons un an.
Le nombre de factures de l'année écoulée correspond à la population à analyser.
Maintenant, si un échantillon complètement aléatoire de 150 factures est tiré de ce groupe, ce serait déjà l'échantillon.
À l'approche des élections, que ce soit au niveau national ou local, les partis politiques font souvent appel à des sociétés spécialisées pour l'analyse des données. De cette manière, ils connaissent l'intention du vote des habitants et planifient des stratégies de campagne appropriées.
Dans ce cas, la population est constituée de tout l'univers des électeurs inscrits dans le système électoral correspondant..
Comme il faudrait beaucoup de temps et d'efforts pour localiser et interroger chaque électeur, les sondeurs choisissent un échantillon d'électeurs à enquêter et à partir de là, extraient les pourcentages et déterminent les tendances..
La sélection de l'échantillon approprié n'est que le début, mais c'est une étape cruciale pour assurer le succès de l'étude..
Personne n'a encore commenté ce post.