
Explication de l'équation de Henderson-Hasselbalch, exemples, exercice
La Équation de Henderson-Hasselbalch est une expression mathématique qui permet le calcul du pH d'un tampon ou d'une solution tampon. Il est basé sur le pKa de l'acide et la relation entre les concentrations de la base ou du sel conjugué et l'acide, présent dans la solution tampon..
L'équation a été initialement développée par Lawrence Joseph Henderson (1878-1942) en 1907. Ce chimiste a établi les composants de son équation basée sur l'acide carbonique comme tampon ou tampon..
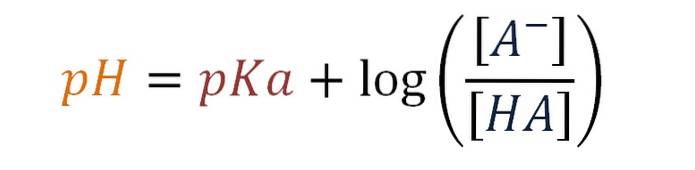
Plus tard, Karl Albert Hasselbalch (1874-1962) a introduit en 1917 l'utilisation de logarithmes pour compléter l'équation de Henderson. Le chimiste danois a étudié les réactions du sang avec l'oxygène et l'effet sur son pH.
Une solution tampon est capable de minimiser les changements de pH qu'une solution subit en ajoutant un volume d'acide fort ou de base. Il est composé d'un acide faible et de sa base conjuguée forte qui se dissocie rapidement.
Index des articles
- 1 Explication
- 1.1 Développement mathématique
- 1.2 Équation pour une base faible
- 2 Comment fonctionne un tampon?
- 2.1 Action d'amortissement
- 2.2 Capacité tampon
- 3 Exemples d'équations de Henderson
- 3.1 Amortisseur en acétate
- 3.2 Tampon acide carbonique
- 3.3 Tampon lactate
- 3.4 Tampon phosphate
- 3.5 Oxyhémoglobine
- 3.6 Désoxyhémoglobine
- 4 exercices résolus
- 4.1 Exercice 1
- 4.2 Exercice 2
- 4.3 Exercice 3
- 5 Références
Explication
Développement mathématique
Un acide faible dans une solution aqueuse se dissocie selon la loi de l'action de masse, selon le schéma suivant:
HA + HdeuxO ⇌ H+ + À-
HA est l'acide faible et A- sa base conjuguée.
Cette réaction est réversible et a une constante d'équilibre (Ka):
Ka = [H+] ·[À-] / [HA]
Prendre des logarithmes:
log Ka = log [H+] + Journal [A-] - journal [HA]
Si chaque terme de l'équation est multiplié par (-1), il est exprimé comme suit:
- log Ka = - log [H+] - journal [A] + journal [HA]
Le - log Ka est défini comme pKa et le - log [H+] est défini comme pH. Après avoir effectué la substitution appropriée, l'expression mathématique se réduit à:
pKa = pH - log [A-] + Journal [HA]
En résolvant les termes de pH et de regroupement, l'équation est exprimée comme suit:
pH = pKa + log [A-] / [HA]
C'est l'équation de Henderson-Hasselbalch pour un tampon acide faible.
Équation pour une base faible
De même, une base faible peut former un tampon, et l'équation de Henderson-Hasselbalch est la suivante:
pOH = pKb + log [HB] / [B-]
Cependant, la plupart des solutions tampons proviennent, même celles d'importance physiologique, de la dissociation d'un acide faible. Par conséquent, l'expression la plus utilisée pour l'équation de Henderson-Hasselbalch est:
pH = pKa + log [A-] / [HA]
Comment fonctionne un tampon?
Action d'amortissement
L'équation de Henderson-Hasselbalch indique que cette solution est constituée d'un acide faible et d'une base conjuguée forte exprimée en sel. Cette composition permet à la solution tampon de rester à un pH stable même lorsque des acides ou des bases forts sont ajoutés..
Lorsqu'un acide fort est ajouté au tampon, il réagit avec la base conjuguée pour former un sel et de l'eau. Cela neutralise l'acide et permet à la variation de pH d'être minimale..
Maintenant, si une base forte est ajoutée au tampon, elle réagit avec l'acide faible et forme de l'eau et un sel, neutralisant l'action de la base ajoutée sur le pH. Par conséquent, la variation de pH est minime.
Le pH d'une solution tampon dépend du rapport des concentrations de la base conjuguée et de l'acide faible, et non de la valeur absolue des concentrations de ces composants. Une solution tampon peut être diluée avec de l'eau et le pH sera pratiquement inchangé.
Capacité tampon
Le pouvoir tampon dépend également du pKa de l'acide faible, ainsi que des concentrations de l'acide faible et de la base conjuguée. Plus le pH du tampon est proche du pKa de l'acide, plus sa capacité tampon est grande..
De même, plus la concentration des composants de la solution tampon est élevée, plus sa capacité tampon est grande..
Exemples d'équations de Henderson
Amortisseur en acétate
pH = pKa + log [CH3ROUCOULER-] / [CH3COOH]
pKa = 4,75
Tampon acide carbonique
pH = pKa + log [HCO3-] / [HdeuxCO3]
pKa = 6,11
Cependant, le processus global qui conduit à la formation de l'ion bicarbonate dans un organisme vivant est le suivant:
COdeux + HdeuxO ⇌ HCO3- + H+
Être le COdeux un gaz, sa concentration en solution est exprimée en fonction de sa pression partielle.
pH = pka + log [HCO3-] / α pCOdeux
α = 0,03 (mmol / L) / mmHg
pCOdeux est la pression partielle de COdeux
Et puis l'équation ressemblerait à:
pH = pKa + log [HCO3-] / 0,03 pCOdeux
Tampon lactate
pH = pKa + log [ion lactate] / [acide lactique]
pKa = 3,86
Tampon phosphate
pH = pKa + log [phosphate dibasique] / [phosphate monobasique]
pH = pKa + log [HPO4deux-] / [HdeuxPO4-]
pKa = 6,8
Oxyhémoglobine
pH = pKa + log [HbOdeux-] / [HHbOdeux]
pKa = 6,62
Désoxyhémoglobine
pH = pKa + log [Hb-] / HbH
pKa = 8,18
Exercices résolus
Exercice 1
Le tampon phosphate joue un rôle important dans la régulation du pH corporel, car son pKa (6,8) est proche du pH existant dans l'organisme (7,4). Quelle sera la valeur de la relation [NadeuxHPO4deux-] / [NaHdeuxPO4-] de l'équation de Henderson-Hasselbalch pour une valeur de pH = 7,35 et un pKa = 6,8?
La réaction de dissociation NaHdeuxPO4- c'est:
NaHdeuxPO4- (acide) ⇌ NaHPO4deux- (base) + H+
pH = pKa + log [NadeuxHPO4deux-] / [NaHdeuxPO4-]
En résolvant le rapport [base conjuguée / acide] pour le tampon phosphate, nous avons:
7,35 - 6,8 = log [NadeuxHPO4deux-] / [NaHdeuxPO4-]
0,535 = log [NadeuxHPO4deux-] / [NaHdeuxPO4-]
dix0,535 = 10journal [Na2HPO4] / [NaH2PO4]
3,43 = [NadeuxHPO4deux-] / [NaHdeuxPO4-]
Exercice 2
Un tampon acétate a une concentration d'acide acétique de 0,0135 M et une concentration d'acétate de sodium de 0,0260 M. Calculer le pH du tampon, sachant que le pKa du tampon acétate est de 4,75.
L'équilibre de dissociation de l'acide acétique est:
CH3COOH ⇌ CH3ROUCOULER- + H+
pH = pKa + log [CH3ROUCOULER-] / [CH3COOH]
En substituant les valeurs que nous avons:
[CH3ROUCOULER-] / [CH3COOH] = 0,0260 M / 0,0135 M
[CH3ROUCOULER-] / [CH3COOH] = 1,884
log 1,884 = 0,275
pH = 4,75 + 0,275
pH = 5,025
Exercice 3
Un tampon acétate contient 0,1 M d'acide acétique et 0,1 M d'acétate de sodium. Calculez le pH du tampon après avoir ajouté 5 ml d'acide chlorhydrique 0,05 M à 10 ml de la solution ci-dessus.
La première étape consiste à calculer la concentration finale du HCl lorsqu'il est mélangé avec la solution tampon:
ViCi = VfCf
Cf = Vi · (Ci / Vf)
= 5 ml · (0,05 M / 15 ml)
= 0,017 M
L'acide chlorhydrique réagit avec l'acétate de sodium pour former de l'acide acétique. Par conséquent, la concentration d'acétate de sodium diminue de 0,017 M et la concentration d'acide acétique augmente de la même quantité:
pH = pKa + log (0,1 M - 0,017 M) / (0,1 M + 0,017 M)
pH = pKa + log 0,083 / 0,017
= 4,75 - 0,149
= 4,601
Les références
- Whitten, Davis, Peck et Stanley. (2008). Chimie. (8e éd.). Apprentissage CENGAGE.
- Jimenez Vargas et J. Mª Macarulla. (1984). Physicochimie physiologique. 6e édition. Éditorial Interamericana.
- Wikipédia. (2020). Équation de Henderson-Hasselbalch. Récupéré de: en.wikipedia.org
- Gurinder Khaira et Alexander Kot. (05 juin 2019). Approximation Henderson-Hasselbalch. Chimie LibreTexts. Récupéré de: chem.libretexts.org
- Helmenstine, Anne Marie, Ph.D. (29 janvier 2020). Définition de l'équation de Henderson Hasselbalch. Récupéré de: thinkco.com
- Les rédacteurs de l'Encyclopaedia Britannica. (6 février 2020). Lawrence Joseph Henderson. Encyclopædia Britannica. Récupéré de: britannica.com



Personne n'a encore commenté ce post.