
Formules et équations d'erreur d'échantillonnage, calcul, exemples
le erreur d'échantillonnage ou alors erreur d'échantillon En statistique, c'est la différence entre la valeur moyenne d'un échantillon et la valeur moyenne de la population totale. Pour illustrer l'idée, imaginons que la population totale d'une ville soit d'un million de personnes, dont la pointure moyenne est souhaitée, pour laquelle un échantillon aléatoire de mille personnes est prélevé.
La taille moyenne qui émerge de l'échantillon ne coïncidera pas nécessairement avec celle de la population totale, même si si l'échantillon n'est pas biaisé, la valeur doit être proche. Cette différence entre la valeur moyenne de l'échantillon et celle de la population totale est l'erreur d'échantillonnage.
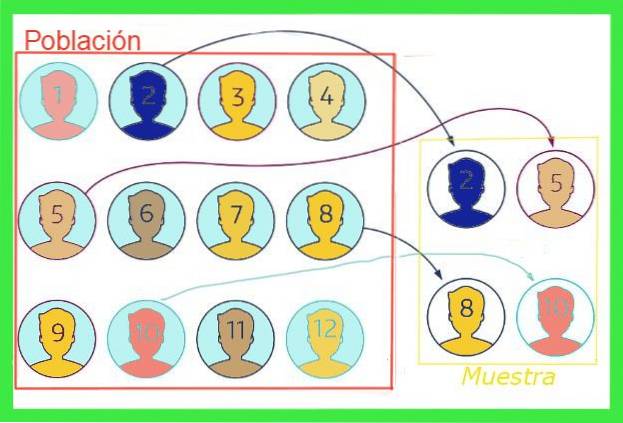
En général, la valeur moyenne de la population totale est inconnue, mais il existe des techniques pour réduire cette erreur et des formules pour estimer la marge d'erreur d'échantillonnage qui sera exposé dans cet article.
Index des articles
- 1 Formules et équations
- 2 Comment calculer l'erreur d'échantillonnage
- 2.1 Pour un niveau de confiance γ
- 3 exemples
- 3.1 - Exemple 1
- 3.2 - Exemple 2
- 3.3 - Exemple 3
- 3.4 - Exemple 4
- 3.5 - Exercice 5
- 4 Références
Formules et équations
Disons que vous voulez connaître la valeur moyenne d'une certaine caractéristique mesurable X dans une population de taille N, mais comment N est un grand nombre, il n'est pas possible de réaliser l'étude sur la population totale, puis on procède à un échantillon aléatoire de taille n<
La valeur moyenne de l'échantillon est notée
Supposons qu'ils prennent m échantillons de la population totale N, tous de la même taille n avec des valeurs moyennes
Ces valeurs moyennes ne seront pas identiques les unes aux autres et seront toutes autour de la valeur moyenne de la population μ. le marge d'erreur d'échantillonnage E indique la séparation attendue des valeurs moyennes
le marge d'erreur standard ε échantillon de taille n c'est:
ε = σ / √n
où σ est l'écart type (la racine carrée de la variance), qui est calculée à l'aide de la formule suivante:
σ = √ [(x -
Le sens de marge d'erreur standard ε est le suivant:
le valeur moyenne
Comment calculer l'erreur d'échantillonnage
Dans la section précédente, la formule a été donnée pour trouver le marge d'erreur la norme d'un échantillon de taille n, où le mot standard indique qu'il s'agit d'une marge d'erreur avec une confiance de 68%.
Cela indique que si de nombreux échantillons de même taille ont été prélevés n, 68% d'entre eux donneront des valeurs moyennes
Il existe une règle simple, appelée le règle 68-95-99.7 ce qui nous permet de trouver la marge de erreur d'échantillonnage E pour les niveaux de confiance de 68%, 95% Oui 99,7% facilement, puisque cette marge est de 1⋅ε, 2⋅ε et 3⋅ε respectivement.
Pour un niveau de confiance γ
Si il niveau de confiance γ n'est pas l'une des réponses ci-dessus, alors l'erreur d'échantillonnage est l'écart type σ multiplié par le facteur Zγ, qui est obtenu par la procédure suivante:
1.- D'abord le niveau de signification α qui est calculé à partir de niveau de confiance γ en utilisant la relation suivante: α = 1 - γ
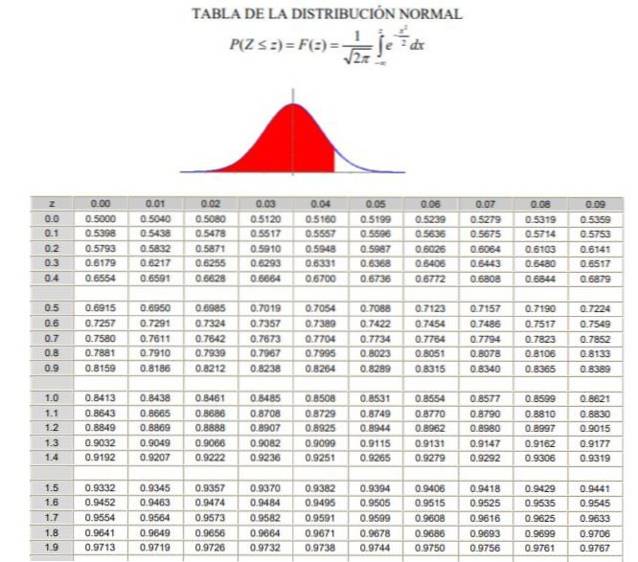
2.- Ensuite, vous devez calculer la valeur 1 - α / 2 = (1 + γ) / 2, qui correspond à la fréquence normale accumulée entre -∞ et Zγ, dans une distribution gaussienne normale ou standardisée F (z), dont la définition est visible sur la figure 2.
3.- L'équation est résolue F (Zγ) = 1 - α / 2 au moyen des tableaux de la distribution normale (cumulative) F, ou au moyen d'une application informatique qui a la fonction gaussienne normalisée inverse F-1.
Dans ce dernier cas, nous avons:
Zγ = G-1(1 - α / 2).
4.- Enfin, cette formule est appliquée pour l'erreur d'échantillonnage avec un niveau de fiabilité γ:
E = Zγ⋅(σ / √n)
Exemples
- Exemple 1
Calculez le marge d'erreur standard dans le poids moyen d'un échantillon de 100 nouveau-nés. Le calcul du poids moyen a été
Solution
le marge d'erreur standard c'est ε = σ / √n = (1500 kg) / √100 = 0,15 kg. Ce qui signifie qu'avec ces données, on peut déduire que le poids de 68% des nouveau-nés est compris entre 2950 kg et 3,25 kg.
- Exemple 2
Déterminer la marge d'erreur d'échantillonnage E et la plage de poids de 100 nouveau-nés avec un niveau de confiance de 95% si le poids moyen est de 3100 kg avec un écart type σ = 1 500 kilogrammes.
Solution
Si la règle 68; 95; 99,7 → 1⋅ε; 2⋅ε; 3⋅ε, vous avez:
E = 2⋅ε = 2⋅0,15 kg = 0,30 kg
Autrement dit, 95% des nouveau-nés auront un poids compris entre 2800 kg et 3400 kg.
- Exemple 3
Déterminez la plage de poids des nouveau-nés à partir de l'exemple 1 avec une marge de confiance de 99,7%.
Solution
L'erreur d'échantillonnage avec une confiance de 99,7% est 3 σ / √n, qui pour notre exemple est E = 3 * 0,15 kg = 0,45 kg. De là, on en déduit que 99,7% des nouveau-nés auront un poids compris entre 2650 kg et 3550 kg.
- Exemple 4
Déterminez le facteur Zγ pour un niveau de fiabilité de 75%. Déterminer la marge d'erreur d'échantillonnage avec ce niveau de fiabilité pour le cas présenté dans l'exemple 1.
Solution
le un niveau de confiance c'est γ = 75% = 0,75 qui est lié à la niveau de signification α à travers la relation γ= (1 - α), de sorte que le niveau de signification soit α = 1 - 0,75 = 0,25.
Cela signifie que la probabilité normale cumulée entre -∞ et Zγ c'est:
P (Z ≤ Zγ ) = 1 - 0,125 = 0,875
Ce qui correspond à une valeur Zγ 1.1503, comme le montre la figure 3.
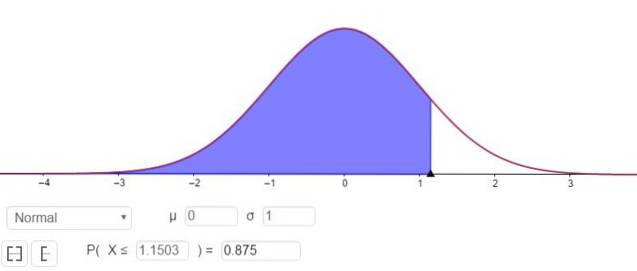
Autrement dit, l'erreur d'échantillonnage est E = Zγ⋅(σ / √n)= 1,15⋅(σ / √n).
Lorsqu'il est appliqué aux données de l'exemple 1, il donne une erreur de:
E = 1,15 * 0,15 kg = 0,17 kg
Avec un niveau de confiance de 75%.
- Exercice 5
Quel est le niveau de confiance si Zα / 2 = 2,4 ?
Solution
P (Z ≤ Zα / 2 ) = 1 - α / 2
P (Z ≤ 2,4) = 1 - α / 2 = 0,9918 → α / 2 = 1 - 0,9918 = 0,0082 → α = 0,0164
Le niveau de signification est:
α = 0,0164 = 1,64%
Et enfin, le niveau de confiance demeure:
1- α = 1 - 0,0164 = 100% - 1,64% = 98,36%
Les références
- Canavos, G. 1988. Probabilité et statistiques: applications et méthodes. Mcgraw Hill.
- Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8ème. Édition. Cengage.
- Levin, R. 1988. Statistiques pour les administrateurs. 2ème. Édition. Prentice Hall.
- Sudman, S. 1982. Poser des questions: un guide pratique pour la conception de questionnaires. San Francisco. Jossey basse.
- Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et les sciences. Pearson.
- Wonnacott, T.H. et R.J. Wonnacott. 1990. Statistiques préliminaires. 5e éd. Wiley
- Wikipédia. Erreur d'échantillonnage. Récupéré de: en.wikipedia.com
- Wikipédia. Marge d'erreur. Récupéré de: en.wikipedia.com



Personne n'a encore commenté ce post.