Statistiques descriptives et inférentielles

La statistiques descriptives C'est l'ensemble des méthodes statistiques qui décrivent et / ou caractérisent un groupe de données. La statistiques déductives cherche à déduire et à tirer des conclusions sur des situations générales au-delà de l'ensemble des données obtenues.

La statistique est une discipline qui est responsable du traitement et de l'organisation des données, les données étant toute mesure ou valeur pouvant être obtenue par des expériences, des enquêtes, des recensements ou d'autres moyens. L'analyse des données commence généralement par l'application de méthodes de statistiques descriptives, puis se poursuit avec des méthodes de statistiques inférentielles..

	Statistiques descriptives	Statistiques déductives
Définition	Méthodes utilisées pour résumer les principales caractéristiques des données connues.	Méthodes qui impliquent l'utilisation d'échantillons de données pour faire des généralisations ou des inférences sur une population.
Objectifs	Caractériser un groupe de données Examiner les tendances ou les distributions	Examiner les différences entre les groupes. Examiner si des variables sont associées. Comparer les moyennes entre les groupes. Prédire une variable à partir d'une autre.
Méthodes d'analyse	Mesures de tendance centrale: Moitié Médian mode Mesures de variabilité: Variance Écart-type Rang La fréquence	test t Analyse de variance Corrélation Régression
Zone d'application	Sciences naturelles et sociales	Sciences sociales et naturelles
Exemples	Caractéristiques des patients pris en charge dans un hôpital. Moyenne et répartition de l'âge, du poids et de la taille des élèves d'une école.	Prédire l'apparition de la démence chez les personnes en fonction de leur état cardiovasculaire. Prouver qu'un médicament agit pour traiter une maladie.

Qu'est-ce que les statistiques descriptives?

La statistiques descriptives C'est la partie des statistiques qui organise les données de manière à ce qu'elles puissent être analysées et interprétées. Les méthodes de statistiques descriptives nous permettent de:

• Détermine le tendance centrale d'une variable: moyenne ou moyenne arithmétique, médiane ou mode.
• Détermine le variabilité d'une variable: écart type, variance, plages.
• Déterminez ce que distribution d'une variable: histogramme de fréquence, distribution normale.

Exemples de statistiques descriptives

Lorsque vous souhaitez caractériser un groupe d'individus, vous utilisez des statistiques descriptives. Par exemple, nous avons les données de température corporelle suivantes pour un groupe d'hommes et de femmes:

Hommes	Femmes
36,1	36,2
35,9	37,2
36,0	37,3
36,4	37,1
36,3	37,0
36,7	37,2
36,9	36,9
36,8	36,8
37,2	36,4
37,0	37,0

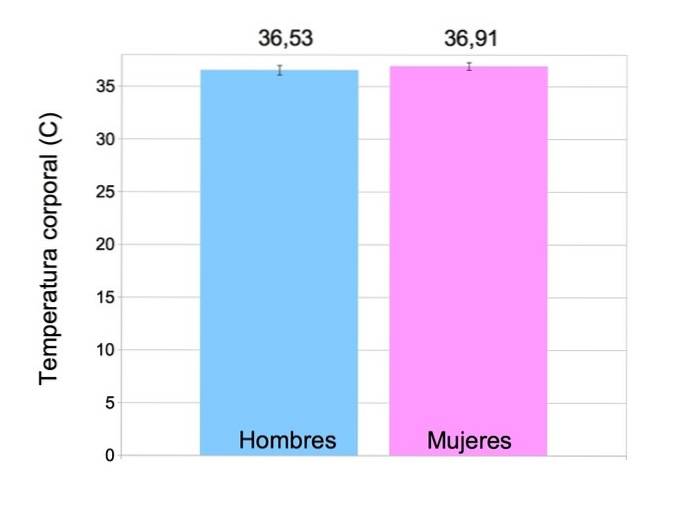
Au fur et à mesure de leur présentation, nous ne pouvons tirer aucune conclusion, mais en appliquant des techniques de statistiques descriptives, nous pouvons alors dire que:

• les hommes de ce groupe ont une température moyenne de 36,53 ° C avec un écart type de 0,45;
• les femmes de ce groupe ont une température moyenne de 36,91 ºC, avec un écart type de 0,36.

Qu'est-ce que les statistiques inférentielles?

La statistiques déductives ou l'inférence statistique est la partie des statistiques qui cherche à prédire ou à déduire les caractéristiques ou les résultats attendus d'une population, sur la base des données obtenues à partir d'un échantillon de cette population. Parmi les techniques appliquées aux statistiques inférentielles, il y a:

• Le test t: permet de comparer la moyenne arithmétique de deux groupes en déterminant si les différences entre les groupes se produisent de manière aléatoire ou systématiquement indiquant une différence réelle.
• Analyse de variance ou ANOVA: appliqué pour comparer deux ou plusieurs groupes de variables.
• L'analyse de corrélation: révèle si les valeurs entre deux variables ont tendance à changer systématiquement. Pour effectuer ces déterminations, le coefficient de corrélation est utilisé r et la valeur de p ou intervalle de confiance CI.
• Analyse de régression: prédit une valeur à partir d'une autre.

Exemples de statistiques inférentielles

Si nous voulons déterminer si un comportement ou un état biologique est associé à une maladie, nous utilisons des méthodes statistiques inférentielles. Par exemple, dans une étude menée en Allemagne, 3109 personnes ont été évaluées pour différents paramètres de santé pendant près de sept ans. Les résultats ont montré qu'une glycémie élevée (supérieure à 126 mg / dl à jeun), le tabagisme et l'inactivité physique étaient associés au développement de la démence..

Lorsqu'un nouveau médicament est découvert et que son efficacité doit être démontrée dans une certaine maladie, des statistiques inférentielles sont utilisées. Dans ce cas, les effets d'un groupe traité avec le médicament et d'un autre groupe traité avec un placebo ou un médicament témoin sont comparés..

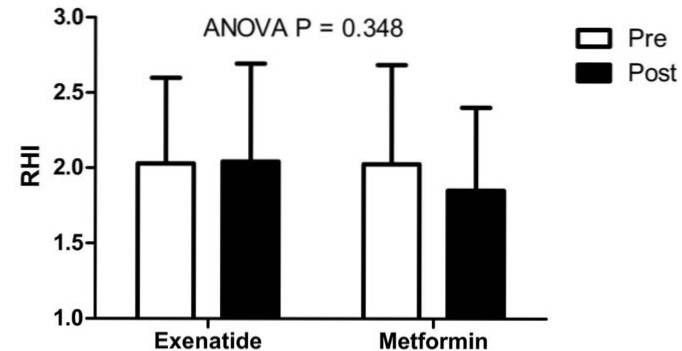
Le groupe de Kelly et al a étudié la fonction endothéliale chez 50 personnes obèses avant (pré) et après (post) trois mois de traitement avec deux médicaments: l'exénatide et la metformine (contrôle). Lors de l'analyse des résultats avec la technique ANOVA (P = 0,348; statistiques inférentielles), ils ont découvert que l'exénatide n'avait aucun effet sur la fonction endothéliale, par rapport à la metformine..

Les références

Hessler, J.B., Ander, K-H, Brönner, M. et al. (2016) Prédire la démence chez les patients en soins primaires avec une métrique de santé cardiovasculaire: une étude prospective basée sur la population. BMC Neurol. 16: 116.

Kelly, A.S., Bergenstal, R.M., Gonzalez-Campoy, J.M., Katz, H., Bank, A.J. (2012) Effets de l'exénatide vs la metformine sur la fonction endothéliale chez les patients obèses atteints de pré-diabète: un essai randomisé. Diabétologie cardiovasculaire 11:64.