
Coefficient de frottement statique, exemple, exercice

La frottement statique est la force qui survient entre deux surfaces lorsqu'une surface ne glisse pas par rapport à l'autre. C'est d'une grande importance, car cela nous permet d'avancer lors de la marche, car c'est la force présente entre le sol et la semelle des chaussures.
C'est aussi le frottement statique qui apparaît entre le trottoir et les pneus de la voiture. Si cette force n'est pas présente, il est alors impossible pour la voiture de commencer à bouger, comme cela se produit dans une voiture qui tente de démarrer sur une surface glacée: les roues glissent mais la voiture ne bouge pas.

Le frottement statique dépend de la rugosité des surfaces en contact et également du type de matériau à partir duquel elles sont fabriquées. C'est pourquoi les pneus et les chaussures de sport sont en caoutchouc, afin d'augmenter le frottement avec la chaussée..
Dans le modèle de friction statique, les caractéristiques des matériaux et le degré de rugosité entre les surfaces sont résumés dans un nombre appelé coefficient de frottement statique, qui est déterminé expérimentalement.
Index des articles
- 1 Coefficient de frottement statique
- 2 Exemple: détermination du coefficient de frottement statique
- 3 Exercice
- 3.1 Solution
- 4 Références
Coefficient de frottement statique

La figure ci-dessus montre un livre au repos sur une table qui a une inclinaison de 15,7 °.
Si les surfaces du livre et de la table étaient très lisses et polies, le livre ne pouvait pas rester immobile. Mais comme ils ne le sont pas, il apparaît une force tangente aux surfaces en contact appelée force de frottement statique.
Si l'angle d'inclinaison est assez grand, alors il n'y a pas assez force de friction statique pour équilibrer le livre et il commencerait à glisser.
Dans ce cas, il y a aussi des frictions entre le livre et la table, mais ce serait un force de friction dynamique, aussi appelé frottement cinétique.
Il existe une frontière entre le frottement statique et le frottement dynamique, qui se produit au moment où le frottement statique atteint sa valeur maximale.
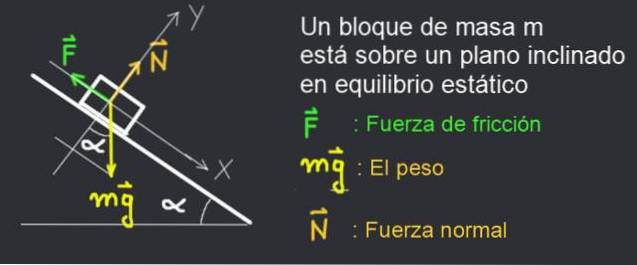
Considérons sur la figure 2, le diagramme de force d'un livre de masse m maintenu au repos sur un plan d'inclinaison α.
Le livre reste au repos car la force de frottement statique F équilibre le système.
Si l'angle d'inclinaison augmente un peu, alors les surfaces en contact doivent fournir plus de force de frottement, mais la quantité de frottement statique que les surfaces en contact peuvent fournir a une limite maximale Fmax, c'est-à-dire:
F ≤ Fmax.
La force de frottement statique maximale dépendra des matériaux et du degré de rugosité des surfaces en contact, ainsi que de la fermeté de la poignée.
Le coefficient de frottement statique μet est un nombre positif qui dépend des caractéristiques des surfaces en contact. Force normale N que le plan exerce sur le bloc montre le degré d'étanchéité entre la surface du bloc et le plan. C'est ainsi qu'ils déterminent la force de frottement maximale que les surfaces fournissent lorsqu'il n'y a pas de glissement:
Fmax = μet N
En résumé, la force de frottement statique suit le modèle suivant:
F ≤ μet N
Exemple: détermination du coefficient de frottement statique
Le coefficient de frottement statique est un nombre sans dimension qui est déterminé expérimentalement pour chaque paire de surfaces.
Nous considérons le bloc au repos sur la figure 2. Les forces suivantes agissent sur lui:
- Force de friction: F
- Le poids du bloc de masse m: mg
- Force normale: N
Comme le bloc est au repos et n'a pas d'accélération, selon la deuxième loi de Newton, la force résultante -une somme vectorielle- est nulle:
F + N + mg = 0
Un système de coordonnées XY fixe est considéré avec l'axe X le long du plan incliné et l'axe Y perpendiculaire à celui-ci, comme le montre la figure 2.
Les forces doivent être séparées selon leurs composantes cartésiennes, donnant lieu au système d'équations suivant:
-Composant X: -F + mg Sen (α) = 0
-Composant Y: N - mg Cos (α) = 0
La valeur de la force de frottement statique est résolue à partir de la première équation:
F = mg Sen (α)
Et à partir de la seconde la valeur de la force normale:
N = mg Cos (α)
La force de frottement statique F obéit au modèle suivant:
F ≤ μet N
En remplaçant les valeurs précédemment obtenues dans l'inégalité, nous avons:
mg Sen (α) ≤ μet mg Cos (α)
En tenant compte du fait que pour des valeurs de α comprises entre 0º et 90º, les fonctions sinus et cosinus sont toutes deux positives, et que le quotient entre le sinus et le cosinus est la tangente, on a:
Tan (α) ≤ μet
L'égalité vaut pour une valeur particulière de α appelée angle critique et que nous notons α *, c'est-à-dire:
μet = Tan (α *)
L'angle critique est déterminé expérimentalement, en augmentant progressivement l'inclinaison jusqu'à l'angle droit auquel le bloc commence à glisser, c'est-à-dire l'angle critique α *.
Dans le livre de la figure 1, cet angle a été déterminé expérimentalement pour donner 24 °. Alors le coefficient de frottement statique est:
μet = Tan (24 °) = 0,45.
C'est un nombre positif compris entre 0 et l'infini. Si μet = 0 les surfaces sont parfaitement lisses. Si μet → ∞ les surfaces sont parfaitement jointes ou soudées.
En général, la valeur du coefficient de frottement est comprise entre 0 et 10.
Exercer
Dans les courses de sprint ou de dragster, des accélérations allant jusqu'à 4g sont obtenues au départ, qui sont réalisées précisément lorsque les pneus ne glissent pas par rapport à la chaussée..
En effet, le coefficient de frottement statique est toujours supérieur au coefficient de frottement dynamique..
En supposant que le poids total du véhicule plus le conducteur est de 600 kg et que les roues arrière supportent 80% du poids, déterminer la force de frottement statique lors du démarrage 4g et le coefficient de frottement statique entre les pneus et la chaussée..

Solution
Selon la deuxième loi de Newton, la force résultante est égale à la masse totale du véhicule multipliée par l'accélération qu'il acquiert.
Le véhicule étant en équilibre vertical, la normale et le poids s'annulent, laissant comme force résultante la force de frottement F que la chaussée exerce sur la zone de contact des roues de traction, laissant que:
F = m (4g) = 600 kg (4 x 9,8 m / sdeux) = 23520 N = 2400 kg-f
Cela signifie que la force de traction est de 2,4 tonnes.
La force de frottement que la roue exerce sur le sol va vers l'arrière, mais sa réaction, qui est la même et opposée, agit sur le pneu et avance. C'est la force qui anime le véhicule.
Bien sûr, toute cette force est produite par le moteur qui tente de repousser le sol à travers la roue, mais la roue et le sol sont couplés par la force de frottement.
Pour déterminer le coefficient de frottement statique on utilise le fait que le F obtenu est le frottement maximal possible, puisque l'on est à la limite de l'accélération maximale, donc:
F = μet N = μe (0,8 mg)
Le fait que les roues motrices arrière supportent 0,8 fois le poids a été pris en compte. En résolvant le coefficient de frottement, nous obtenons:
μet = F / (0,8 mg) = 23520 N / (0,8 x 600 kg x 9,8 m / s ^ 2) = 5.
Conclusion: μet = 5.
Les références
- Alonso M., Finn E. 1970. Physique volume I: Mécanique. Fonds interaméricain pour l'éducation S.A.
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
- Hewitt, P. 2012. Science physique conceptuelle. Cinquième édition.
- Rex, A. 2011. Fondamentaux de la physique. Pearson. 190-200.
- Jeune, Hugh. 2015. Physique universitaire et physique moderne. 14e éd. Pearson.



Personne n'a encore commenté ce post.