Degrés de liberté comment les calculer, types, exemples

Les degrés de liberté en statistique, il s'agit du nombre de composantes indépendantes d'un vecteur aléatoire. Si le vecteur a n composants et il y a p équations linéaires qui relient leurs composantes, puis les degré de liberté est n-p.

Le concept de degrés de liberté Il apparaît également en mécanique théorique, où ils sont à peu près équivalents à la dimension de l'espace où la particule se déplace, moins le nombre de liaisons..

Cet article abordera le concept de degrés de liberté appliqué aux statistiques, mais un exemple mécanique est plus facile à visualiser sous forme géométrique.

Index des articles

• 1 Types de degrés de liberté
  • 1.1 Dans un boîtier mécanique
  • 1.2 Dans un ensemble de valeurs aléatoires
• 2 exemples
  • 2.1 Variance et degrés de liberté
  • 2.2 Dans la distribution du Chi carré
  • 2.3 Dans le test d'hypothèse (avec exemple élaboré)
• 3 Références

Types de degrés de liberté

Selon le contexte dans lequel il est appliqué, la façon de calculer le nombre de degrés de liberté peut varier, mais l'idée sous-jacente est toujours la même: dimensions totales moins nombre de restrictions.

Dans un coffret mécanique

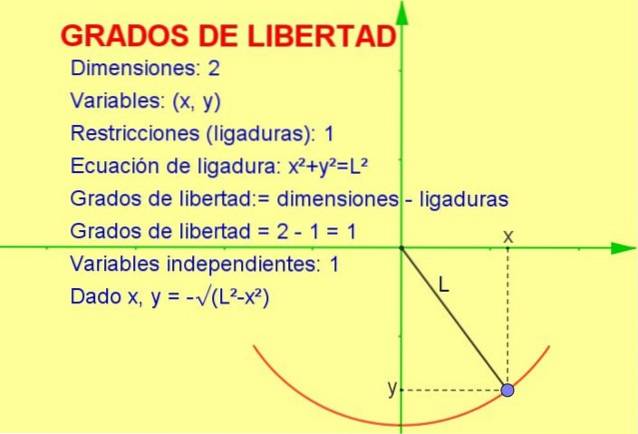
Considérons une particule oscillante liée à une corde (un pendule) qui se déplace dans le plan vertical x-y (2 dimensions). Cependant, la particule est obligée de se déplacer sur la circonférence du rayon égal à la longueur de la corde.

Puisque la particule ne peut se déplacer que sur cette courbe, le nombre de degrés de liberté est 1. Cela peut être vu dans la figure 1.

La façon de calculer le nombre de degrés de liberté est de prendre la différence du nombre de dimensions moins le nombre de contraintes:

degrés de liberté: = 2 (dimensions) - 1 (ligature) = 1

Une autre explication qui nous permet d'arriver au résultat est la suivante:

-On sait que la position en deux dimensions est représentée par un point de coordonnées (x, y).

-Mais puisque le point doit satisfaire l'équation de la circonférence (x^deux + Oui^deux = L^deux) pour une valeur donnée de la variable x, la variable y est déterminée par ladite équation ou restriction.

Ainsi, une seule des variables est indépendante et le système a un (1) degré de liberté.

Dans un ensemble de valeurs aléatoires

Pour illustrer ce que signifie le concept, supposons que le vecteur

X = (x₁, X_deux,..., X_n)

Que représente l'échantillon de n valeurs aléatoires normalement distribuées. Dans ce cas, le vecteur aléatoire X avoir n composants indépendants et donc on dit que X avoir n degrés de liberté.

Maintenant, construisons le vecteur r de déchets

r = (x₁ - , X_deux - ,…., X_n - )

Où représente la moyenne de l'échantillon, calculée comme suit:

= (x₁ + X_deux +…. + X_n) / n

Donc la somme

(X₁ - ) + (x_deux - ) +…. + (X_n - ) = (x₁ + X_deux +…. + X_n) - n= 0

C'est une équation qui représente une contrainte (ou une liaison) sur les éléments du vecteur r des résidus, car si n-1 composants du vecteur sont connus r, l'équation de contrainte détermine le composant inconnu.

Par conséquent, le vecteur r de dimension n avec la restriction:

∑ (x_je - ) = 0

Avoir (n - 1) degrés de liberté.

Encore une fois, il est appliqué que le calcul du nombre de degrés de liberté est:

degrés de liberté: = n (dimensions) - 1 (contraintes) = n-1

Exemples

Variance et degrés de liberté

La variance s^deux est définie comme la moyenne du carré des écarts (ou résidus) de l'échantillon de n données:

s^deux = (r•r) / (n-1)

où r est le vecteur des résidus r = (x1 - , x2 - ,…., Xn - ) et le point épais (•) est l'opérateur produit scalaire. Alternativement, la formule de variance peut être écrite comme suit:

s^deux = ∑ (x_je - )^deux / (n-1)

Dans tous les cas, il convient de noter que lors du calcul de la moyenne du carré des résidus, elle est divisée par (n-1) et non par n, car comme indiqué dans la section précédente, le nombre de degrés de liberté du vecteur r est (n-1).

Si pour le calcul de la variance ont été divisés par n au lieu de (n-1), le résultat aurait un biais très significatif pour les valeurs de n moins de 50.

Dans la littérature, la formule de variance apparaît également avec le diviseur n au lieu de (n-1), lorsqu'il s'agit de la variance d'une population.

Mais l'ensemble de la variable aléatoire des résidus, représentée par le vecteur r, Bien qu'il ait une dimension n, il n'a que (n-1) degrés de liberté. Cependant, si le nombre de données est suffisamment grand (n> 500), les deux formules convergent vers le même résultat.

Les calculatrices et les feuilles de calcul fournissent les deux versions de la variance et de l'écart type (qui est la racine carrée de la variance).

Notre recommandation, au vu de l'analyse présentée ici, est de toujours choisir la version avec (n-1) à chaque fois qu'il est nécessaire de calculer la variance ou l'écart type, pour éviter des résultats biaisés..

Dans la distribution du chi carré

Certaines distributions de probabilité en variable aléatoire continue dépendent d'un paramètre appelé degré de liberté, est le cas de la distribution du Chi carré (χ^deux).

Le nom de ce paramètre provient précisément des degrés de liberté du vecteur aléatoire sous-jacent auquel s'applique cette distribution.

Supposons que nous ayons g populations, à partir desquelles des échantillons de taille n sont prélevés:

X₁ = (x1₁, x1_deux,… X1_n)

X2 = (x2₁, x2_deux,… X2_n)

... .

X_j = (xj₁, xj_deux,… Xj_n)

... .

Xg = (xg₁, xg_deux,… Xg_n)

Une population j qu'est-ce que la moyenne et écart type Sj, suit la distribution normale N (, Sj ).

La variable standardisée ou normalisée zj_je est défini comme:

zj_je = (xj_je - ) / Sj.

Et le vecteur Zj est défini comme ceci:

Zj = (zj₁, zj_deux,..., zj_je,..., zj_n) et suit la distribution normale normalisée N (0,1).

Donc la variable:

Q = ((z1₁ ^ 2 + z2₁^ 2 +…. + zg₁^ 2),…., (Z1_n^ 2 + z2_n^ 2 +…. + zg_n^ 2))

suivre la distribution χ^deux(g) appelé le distribution du chi carré avec degré de liberté g.

Dans le test d'hypothèse (avec exemple élaboré)

Lorsque vous souhaitez tester des hypothèses basées sur un certain ensemble de données aléatoires, vous devez connaître le nombre de degrés de liberté g pour pouvoir appliquer le test du Chi carré.

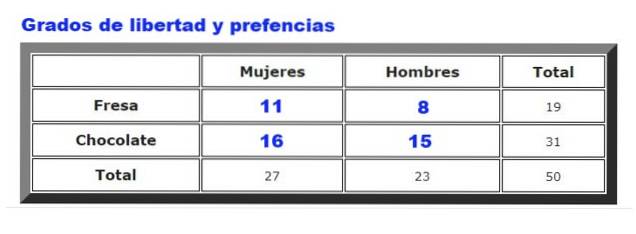
A titre d'exemple, les données collectées sur les préférences de glace au chocolat ou à la fraise chez les hommes et les femmes dans un certain glacier seront analysées. La fréquence à laquelle les hommes et les femmes choisissent la fraise ou le chocolat est résumée dans la figure 2.

Tout d'abord, le tableau des fréquences attendues est calculé, qui est préparé en multipliant le total de lignes pour lui total des colonnes, divisé par données totales. Le résultat est illustré dans la figure suivante:

Ensuite, nous procédons au calcul du Chi carré (à partir des données) en utilisant la formule suivante:

χ^deux = ∑ (F_{ou alors} - F_et)^deux / F_et

Où F_{ou alors} sont les fréquences observées (Figure 2) et F_et sont les fréquences attendues (Figure 3). La sommation couvre toutes les lignes et colonnes, ce qui dans notre exemple donne quatre termes.

Après avoir effectué les opérations, vous obtenez:

χ^deux = 0,2043.

Maintenant, il est nécessaire de comparer avec le Chi carré théorique, qui dépend du nombre de degrés de liberté g.

Dans notre cas, ce nombre est déterminé comme suit:

g = (# lignes - 1) (# colonnes - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Il s'avère que le nombre de degrés de liberté g dans cet exemple est de 1.

Si vous souhaitez vérifier ou rejeter l'hypothèse nulle (H0: il n'y a pas de corrélation entre TASTE et GENDER) avec un niveau de signification de 1%, la valeur théorique du Chi carré est calculée avec le degré de liberté g = 1.

La valeur recherchée rend la fréquence accumulée (1 - 0,01) = 0,99, soit 99%. Cette valeur (qui peut être obtenue à partir des tableaux) est 6,636.

Lorsque le Chi théorique dépasse celui calculé, alors l'hypothèse nulle est vérifiée.

Autrement dit, avec les données collectées, Pas observé relation entre les variables TASTE et GENDER.

Les références

1. Minitab. Quels sont les degrés de liberté? Récupéré de: support.minitab.com.
2. Moore, David. (2009) Statistiques appliquées de base. Éditeur Antoni Bosch.
3. Leigh, Jennifer. Comment calculer les degrés de liberté dans les modèles statistiques. Récupéré de: geniolandia.com
4. Wikipédia. Degré de liberté (statistiques). Récupéré de: es.wikipedia.com
5. Wikipédia. Degré de liberté (physique). Récupéré de: es.wikipedia.com