
Propriétés de l'heptadécagone, diagonales, périmètre, aire

le heptadécagone est un polygone régulier avec 17 côtés et 17 sommets. Sa construction peut être faite dans le style euclidien, c'est-à-dire en utilisant uniquement la règle et la boussole. C'est le grand génie mathématique Carl Friedrich Gauss (1777-1855), à peine 18 ans, qui trouva la procédure de sa construction en 1796.
Apparemment, Gauss a toujours été très enclin à cette figure géométrique, à tel point que dès le jour où il a découvert sa construction, il a décidé d'être mathématicien. On dit aussi qu'il voulait que l'heptadécagone soit gravé sur sa pierre tombale.

Gauss a également trouvé la formule pour déterminer quels polygones réguliers ont la possibilité d'être construits avec une règle et une boussole, car certains n'ont pas de construction euclidienne exacte..
Index des articles
- 1 Caractéristiques de l'heptadécagone
- 2 diagonales et périmètre
- 2.1 Périmètre de l'heptadécagone
- 3 Zone
- 3.1 Zone donnée le côté
- 3.2 Zone compte tenu du rayon
- 4 exemples
- 4.1 Exemple 1
- 4.2 Exemple 2
- 5 Références
Caractéristiques de l'heptadécagone
Quant à ses caractéristiques, comme tout polygone, la somme de ses angles internes est importante. Dans un polygone régulier de n côtés, la somme est donnée par:
Sa (n) = (n -2) * 180º.
Pour l'heptadécagone le nombre de côtés n c'est 17, ce qui signifie que la somme de ses angles internes est:
Sa (17) = (17 - 2) * 180º = 15 * 180º = 2700º.
Cette somme, exprimée en radians, ressemble à ceci:
Sa (17) = (17 - 2) * π = 15 * π = 15π
À partir des formules ci-dessus, on peut facilement déduire que chaque angle interne d'un heptadécagone a une mesure exacte α donnée par:
α = 2700º / 17 = (15/17) π radians
Il s'ensuit que l'angle interne sous forme approximative est:
α ≈ 158 824º
Diagonales et périmètre
Les diagonales et le périmètre sont d'autres aspects importants. Dans tout polygone, le nombre de diagonales est:
D = n (n - 3) / 2 et dans le cas de l'heptadécagone, comme n = 17, c'est alors que D = 119 diagonales.
D'autre part, si la longueur de chaque côté de l'heptadécagone est connue, alors le périmètre de l'heptadécagone régulier est trouvé simplement en ajoutant 17 fois cette longueur, ou ce qui équivaut à 17 fois la longueur ré De chaque côté:
P = 17 j
Périmètre de l'heptadécagone
Parfois, seul le rayon est connu r de l'heptadécagon, il est donc nécessaire de développer une formule pour ce cas.
À cette fin, le concept de apothème. L'apothème est le segment qui va du centre du polygone régulier au milieu d'un côté. L'apothème par rapport à un côté est perpendiculaire à ce côté (voir figure 2).
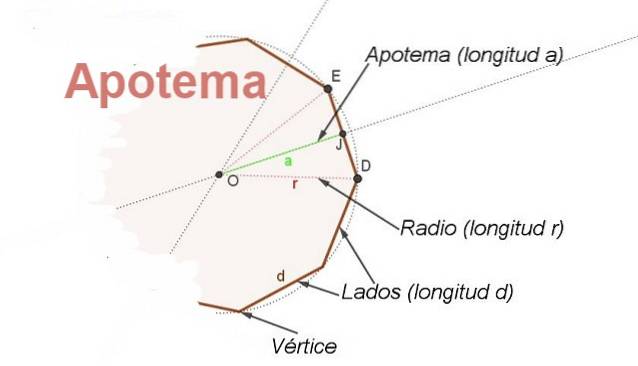
De plus, l'apothème est la bissectrice de l'angle avec le sommet central et les côtés sur deux sommets consécutifs du polygone, cela permet de trouver une relation entre le rayon r et le côté ré.
S'il s'appelle β à l'angle central BICHE et en tenant compte du fait que l'apothème JO est la bissectrice que vous avez EJ = d / 2 = r Sen (β / 2), d'où il y a une relation pour trouver la longueur ré sur le côté d'un polygone connu son rayon r et son angle central β:
d = 2 r Sen (β / 2)
Dans le cas de l'heptadécagone β = 360º / 17 donc vous avez:
d = 2 r Sen (180º / 17) ≈ 0,3675 r
Enfin, on obtient la formule du périmètre de l'heptadécagone, connu son rayon:
P = 34 r Sen (180º / 17) ≈ 6,2475 r
Le périmètre d'un heptadécagone est proche du périmètre de la circonférence qui l'entoure, mais sa valeur est plus petite, c'est-à-dire que le périmètre du cercle circonscrit est Pcir = 2π r ≈ 6,2832 r.
Surface
Pour déterminer l'aire de l'heptadécagone, nous nous référerons à la figure 2, qui montre les côtés et l'apothème d'un polygone régulier de n côtés. Dans cette figure, le triangle EOD a une superficie égale à la base ré (côté du polygone) multiplié par la hauteur à (polygone apothème) diviser par deux:
Zone EOD = (d x a) / 2
Si connu l'apothème à de l'heptadécagone et du côté ré sa superficie est:
Aire de l'heptadécagone = (17/2) (d x a)
Zone compte tenu du côté
Pour obtenir une formule de l'aire de l'heptadécagone connaissant la longueur de ses dix-sept côtés, il est nécessaire d'obtenir une relation entre la longueur de l'apothème à et le côté ré.
En référence à la figure 2, la relation trigonométrique suivante est obtenue:
Tan (β / 2) = EJ / OJ = (d / 2) / a, étant β à l'angle central BICHE. Alors l'apothème à peut être calculé si la longueur est connue ré du côté du polygone et de l'angle central β:
a = (d / 2) Cotan (β / 2)
Si cette expression est maintenant substituée à l'apothème, dans la formule de l'aire de l'heptadécagon obtenue dans la section précédente, on a:
Aire de l'heptadécagone = (17/4) (ddeux) Cotan (β / 2)
Étant β = 360º / 17 pour l'heptadécagone, nous avons donc enfin la formule souhaitée:
Aire de l'heptadécagone = (17/4) (ddeux) Cotan (180º / 17)
Zone compte tenu du rayon
Dans les sections précédentes, une relation avait été trouvée entre le côté d d'un polygone régulier et son rayon r, cette relation étant la suivante:
d = 2 r Sen (β / 2)
Cette expression pour ré est introduit dans l'expression obtenue dans la section précédente pour la zone. Si les substitutions et simplifications pertinentes sont effectuées, la formule qui permet de calculer l'aire de l'heptadécagone est obtenue:
Aire de l'heptadécagone = (17/2) (rdeux) Sen (β) = (17/2) (rdeux) Sen (360º / 17)
Une expression approximative de la zone est:
Surface de l'heptadécagone = 3,0706 (rdeux)
Comme prévu, cette zone est légèrement plus petite que la zone du cercle qui circonscrit l'heptadécagone. Àcirc = π rdeux ≈ 3,1416 rdeux. Pour être précis, il est inférieur de 2% à celui de son cercle circonscrit.
Exemples
Exemple 1
Pour qu'un heptadécagone ait des côtés de 2 cm, quelle doit être la valeur du rayon et du diamètre de la circonférence circonscrite? Trouvez également la valeur du périmètre.
Pour répondre à la question, il est nécessaire de se souvenir de la relation entre le côté et le rayon d'un polygone régulier à n côtés:
d = 2 r Sen (180 ° / n)
Pour l'heptadécagone n = 17, Pour ce que d = 0,3675 r, c'est-à-dire que le rayon de l'heptadécagone est r = 2 cm / 0,3675 = 5,4423 cm ou
10,8844 cm de diamètre.
Le périmètre d'un heptadécagone latéral de 2 cm est P = 17 * 2 cm = 34 cm.
Exemple 2
Quelle est l'aire d'un heptadécagone régulier avec un côté de 2 cm?
Il faut se référer à la formule montrée dans la section précédente, qui nous permet de trouver l'aire d'un heptadécagone quand il a la longueur ré de votre côté:
Aire de l'heptadécagone = (17/4) (ddeux) / Tan (180 ° / 17)
Lors du remplacement d = 2 cm dans la formule ci-dessus, vous obtenez:
Surface = 90,94 cm
Les références
- C. E. A. (2003). Éléments de géométrie: avec exercices et géométrie de la boussole. Université de Medellin.
- Campos, F., Cerecedo, F. J. (2014). Mathématiques 2. Grupo Editorial Patria.
- Libéré, K. (2007). Découvrez les polygones. Benchmark Education Company.
- Hendrik, V. (2013). Polygones généralisés. Birkhäuser.
- IGER. (s.f.). Mathématiques Premier semestre Tacaná. IGER.
- Géométrie Jr. (2014). Polygones. Lulu Press, Inc.
- Miller, Heeren et Hornsby. (2006). Mathématiques: raisonnement et applications (dixième édition). Éducation Pearson.
- Patiño, M. (2006). Mathématiques 5. Progreso éditorial.
- Sada, M. Polygone régulier à 17 côtés avec règle et boussole. Récupéré de: geogebra.org
- Wikipédia. Heptadécagon. Récupéré de: es.wikipedia.com



Personne n'a encore commenté ce post.