La homoscédasticité dans un modèle statistique prédictif il se produit si dans tous les groupes de données d'une ou plusieurs observations, la variance du modèle par rapport aux variables explicatives (ou indépendantes) reste constante.
Un modèle de régression peut être homoscédastique ou non, auquel cas on parle de hétéroscédasticité.
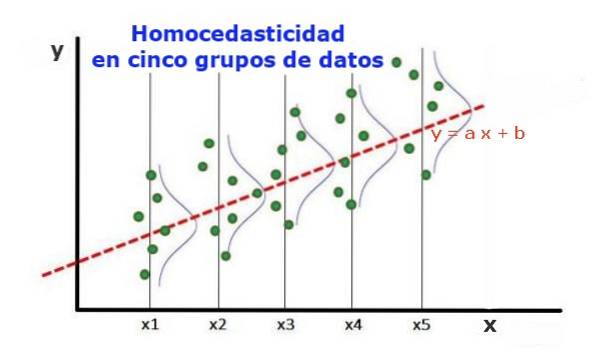
Un modèle de régression statistique de plusieurs variables indépendantes est appelé homoscédastique, uniquement si la variance de l'erreur de la variable prédite (ou l'écart type de la variable dépendante) reste uniforme pour différents groupes de valeurs des variables explicatives ou indépendantes.
Dans les cinq groupes de données de la figure 1, la variance dans chaque groupe a été calculée, par rapport à la valeur estimée par la régression, ce qui fait qu'elle est la même dans chaque groupe. On suppose en outre que les données suivent la distribution normale.
Au niveau graphique, cela signifie que les points sont également dispersés ou dispersés autour de la valeur prédite par l'ajustement de régression, et que le modèle de régression a la même erreur et la même validité pour la plage de la variable explicative..
Index des articles
Pour illustrer l'importance de l'homoscédasticité dans les statistiques prédictives, il faut contraster avec le phénomène inverse, l'hétéroscédasticité.
Dans le cas de la figure 1, dans laquelle il y a homoscédasticité, il est vrai que:
Var ((y1-Y1); X1) ≈ Var ((y2-Y2); X2) ≈… Var ((y4-Y4); X4)
Où Var ((yi-Yi); Xi) représente la variance, la paire (xi, yi) représente les données du groupe i, tandis que Yi est la valeur prédite par la régression pour la valeur moyenne Xi du groupe. La variance des n données du groupe i est calculée comme suit:
Var ((yi-Yi); Xi) = ∑j (yij - Yi) ^ 2 / n
Au contraire, en cas d'hétéroscédasticité, le modèle de régression peut ne pas être valide pour toute la région dans laquelle il a été calculé. La figure 2 montre un exemple de cette situation.
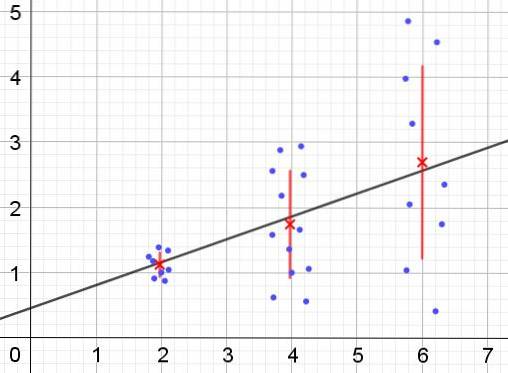
La figure 2 représente trois groupes de données et l'ajustement de l'ensemble à l'aide d'une régression linéaire. Il est à noter que les données des deuxième et troisième groupes sont plus dispersées que dans le premier groupe. Le graphique de la figure 2 montre également la valeur moyenne de chaque groupe et sa barre d'erreur ± σ, avec l'écart type σ de chaque groupe de données. Il faut se rappeler que l'écart type σ est la racine carrée de la variance.
Es claro que en el caso de la heterocedasticidad, el error de la estimación por regresión es cambiante en el rango de valores de la variable explicativa o independiente, y en los intervalos donde este error es muy grande, la predicción por regresión es poco confiable o non applicable.
Dans un modèle de régression, les erreurs ou résidus (et -Y) doivent être distribués avec une variance égale (σ ^ 2) dans l'intervalle de valeurs de la variable indépendante. C'est pour cette raison qu'un bon modèle de régression (linéaire ou non linéaire) doit passer le test d'homoscédasticité..
Les points représentés sur la figure 3 correspondent aux données d'une étude qui cherche une relation entre les prix (en dollars) des maisons en fonction de la taille ou de la superficie en mètres carrés.
Le premier modèle à tester est celui d'une régression linéaire. En premier lieu, on note que le coefficient de détermination R ^ 2 de l'ajustement est assez élevé (91%), on peut donc penser que l'ajustement est satisfaisant..
Cependant, deux régions peuvent être clairement distinguées du graphique d'ajustement. L'un d'eux, celui de droite enfermé dans un ovale, remplit l'homoscédasticité, tandis que la région de gauche n'a pas d'homoscédasticité.
Cela signifie que la prédiction du modèle de régression est adéquate et fiable dans la plage comprise entre 1 800 m ^ 2 et 4 800 m ^ 2, mais très insuffisante en dehors de cette région. Dans la zone hétéroscédastique, non seulement l'erreur est très grande, mais aussi les données semblent suivre une tendance différente de celle proposée par le modèle de régression linéaire..
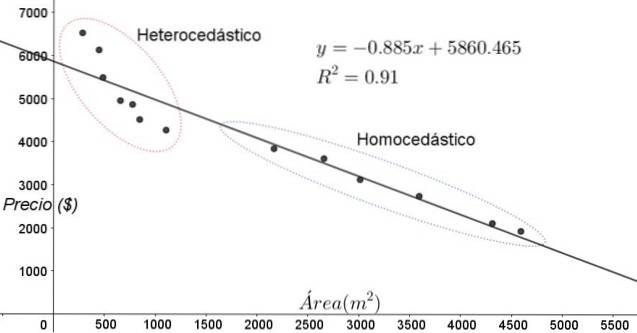
Le nuage de points des données est le test le plus simple et le plus visuel de leur homoscédasticité, mais dans les cas où il n'est pas aussi évident que dans l'exemple illustré à la figure 3, il est nécessaire de recourir à des graphiques avec des variables auxiliaires..
Afin de séparer les zones où l'homoscédasticité est satisfaite et celles où elle ne l'est pas, les variables standardisées ZRes et ZPred sont introduites:
ZRes = Abs (y - Y) / σ
ZPred = Y / σ
Il est à noter que ces variables dépendent du modèle de régression appliqué, puisque Y est la valeur de la prédiction de régression. Vous trouverez ci-dessous le nuage de points ZRes vs ZPred pour le même exemple:
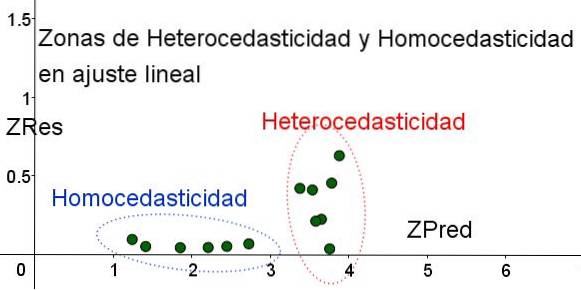
Dans le graphique de la figure 4 avec les variables normalisées, la zone où l'erreur résiduelle est faible et uniforme est clairement séparée de la zone où elle ne l'est pas. Dans la première zone, l'homoscédasticité est remplie tandis que dans la région où l'erreur résiduelle est très variable et importante, l'hétéroscédasticité est remplie..
L'ajustement de régression est appliqué au même groupe de données dans la figure 3, dans ce cas l'ajustement est non linéaire, puisque le modèle utilisé implique une fonction potentielle. Le résultat est illustré dans la figure suivante:
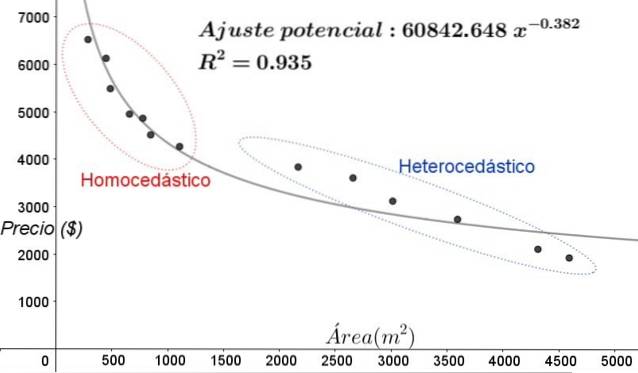
Dans le graphique de la figure 5, les zones homoscédastiques et hétéroscédastiques doivent être clairement notées. Il convient également de noter que ces zones étaient interchangées par rapport à celles qui ont été formées dans le modèle d'ajustement linéaire.
Dans le graphique de la figure 5, il est évident que même lorsque le coefficient de détermination de l'ajustement est assez élevé (93,5%), le modèle n'est pas adéquat pour tout l'intervalle de la variable explicative, puisque les données pour des valeurs supérieures à 2000 m ^ 2 hétéroscédasticité présente.
L'un des tests non graphiques les plus utilisés pour vérifier si l'homoscédasticité est satisfaite ou non est la Test de Breusch-Pagan.
Tous les détails de ce test ne seront pas donnés dans cet article, mais ses caractéristiques fondamentales et les étapes de celui-ci sont décrites en gros traits:
La plupart des progiciels statistiques tels que: SPSS, MiniTab, R, Python Pandas, SAS, StatGraphic et plusieurs autres intègrent le test d'homoscédasticité de Breusch-Pagan. Un autre test pour vérifier l'uniformité de la variance Test de Levene.
Personne n'a encore commenté ce post.