
Formules d'induction magnétique, mode de calcul et exemples
La induction magnétique ou la densité de flux magnétique est une altération de l'environnement provoquée par la présence de courants électriques. Ils modifient la nature de l'espace qui les entoure, créant un Campagne vecteur.
Le vecteur induction magnétique, densité de flux magnétique ou simplement champ magnétique B, il a trois caractéristiques distinctives: une intensité exprimée par une valeur numérique, une direction et aussi un sens donné en chaque point de l'espace. Il est mis en évidence en gras pour le distinguer des quantités purement numériques ou scalaires.
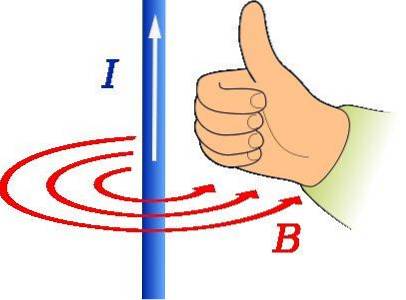
La règle du pouce droit est utilisée pour trouver la direction et la direction du champ magnétique causé par un fil porteur de courant, comme indiqué dans la figure ci-dessus.
Le pouce de la main droite doit pointer dans la direction du courant. Ensuite, la rotation des quatre doigts restants indique la forme de B, qui sur la figure est représenté par les cercles rouges concentriques.
Dans un tel cas, l'adresse de B est tangent à la circonférence concentrique avec le fil et est dans le sens antihoraire.
La induction magnétique B Dans le système international, Tesla (T) est mesuré, mais il est plus fréquent de le mesurer dans une autre unité appelée Gauss (G). Les deux unités ont été nommées respectivement en l'honneur de Nikola Tesla (1856-1943) et Carl Friedrich Gauss (1777-1855) pour leurs contributions extraordinaires à la science de l'électricité et du magnétisme..
Index des articles
- 1 Quelles sont les propriétés de l'induction magnétique ou de la densité de flux magnétique?
- 2 Loi de Biot-Savart
- 3 formules
- 4 Comment est-il calculé?
- 4.1 Exemple
- 5 Références
Quelles sont les propriétés de l'induction magnétique ou de la densité de flux magnétique?
Une boussole placée près d'un fil sous tension s'alignera toujours avec B. Le physicien danois Hans Christian Oersted (1777-1851) a été le premier à remarquer ce phénomène au début du 19e siècle.
Et lorsque le courant cesse, la boussole pointe à nouveau vers le nord géographique, comme toujours. En changeant soigneusement la position de la boussole, une carte de la forme du champ magnétique est obtenue.
Cette carte a toujours la forme de cercles concentriques au fil, comme décrit au début. De cette façon, vous pouvez visualiser B.
Même si le fil n'est pas droit, le vecteur B il formera des cercles concentriques autour de lui. Pour déterminer la forme du champ, imaginez simplement de très petits segments de fil, si petits qu'ils semblent rectilignes et entourés de cercles concentriques..
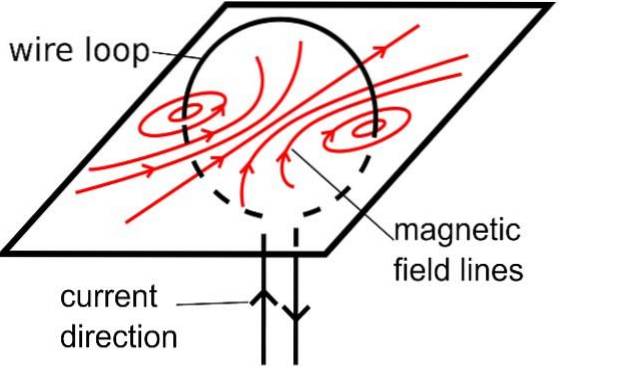
Cela indique une propriété importante des lignes de champ magnétique. B: ils n'ont ni début ni fin, ce sont toujours des courbes fermées.
Loi de Biot-Savart
Le 19e siècle a marqué le début de l'ère de l'électricité et du magnétisme dans la science. Vers 1820, les physiciens français Jean Marie Biot (1774-1862) et Félix Savart (1791-1841) découvrent la loi qui porte leur nom et qui permet de calculer le vecteur B.
Ils ont fait les observations suivantes sur la contribution au champ magnétique produit par un segment de fil de longueur différentielle dl qui transporte un courant électrique je:
- L'ampleur de B diminue avec l'inverse du carré de la distance au fil (cela a du sens: loin du fil, l'intensité de B doit être inférieur aux points proches).
- L'ampleur de B est proportionnel à l'intensité du courant je qui passe par le fil.
- L'adresse de B est tangent à la circonférence du rayon r centré sur le fil et le sens de B est donnée, comme nous l'avons dit, par la règle du pouce droit.
Le produit croisé ou produit croisé est l'outil mathématique approprié pour exprimer le dernier point. Pour établir un produit vectoriel, deux vecteurs sont nécessaires, qui sont définis comme suit:
- rél est le vecteur dont la magnitude est la longueur du segment différentiel dl
- r est le vecteur qui va du fil au point où vous voulez trouver le champ
Formules
Tout cela peut être combiné dans une expression mathématique:

La constante de proportionnalité nécessaire pour établir l'égalité est la perméabilité magnétique de l'espace libre μou alors = 4π.10-7 T.m / A
Cette expression est la loi de Biot et Savart, qui permet de calculer le champ magnétique d'un segment courant.
Un tel segment doit à son tour faire partie d'un circuit plus grand et plus fermé: une distribution de courant.
La condition que le circuit est fermé est nécessaire pour qu'un courant électrique circule. Le courant électrique ne peut pas circuler dans les circuits ouverts.
Enfin, pour trouver le champ magnétique total de ladite distribution de courant, toutes les contributions de chaque segment différentiel sont ajoutées rél. Cela équivaut à intégrer sur toute la distribution:

Pour appliquer la loi de Biot-Savart et calculer le vecteur d'induction magnétique, il est nécessaire de considérer quelques points importants très importants:
- Le produit croisé entre deux vecteurs aboutit toujours à un autre vecteur.

- Il est pratique de trouver le produit vectoriel avant que passer à la résolution de l'intégrale, alors l'intégrale de chacun des composants obtenue séparément est résolue.
- Il est nécessaire de dessiner une image de la situation et d'établir un système de coordonnées approprié.
- Chaque fois que l'existence d'une symétrie est observée, elle doit être utilisée pour gagner du temps de calcul.
- Lorsqu'il y a des triangles, le théorème de Pythagore et le théorème du cosinus sont d'une grande aide pour établir la relation géométrique entre les variables.
Comment est-il calculé?
Avec un exemple pratique du calcul de B pour un fil droit, ces recommandations s'appliquent.
Exemple
Calculez le vecteur de champ magnétique qu'un très long fil rectiligne produit en un point P dans l'espace, selon la figure ci-contre.

À partir de la figure, vous devez:
- Le fil est dirigé dans une direction verticale, le courant I circulant vers le haut. Cette direction est + y dans le système de coordonnées, dont l'origine est au point O.
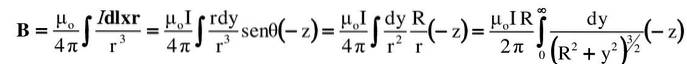
- Dans un tel cas, selon la règle du pouce droit, B au point P, il est dirigé vers l'intérieur du papier, c'est pourquoi il est désigné par un petit cercle et un «x» sur la figure. Cette adresse sera prise comme -z.
- Le triangle rectangle dont les jambes sont Oui Oui R, reliez les deux variables selon le théorème de Pythagore: rdeux= Rdeux+Ouideux
Tout cela est substitué dans l'intégrale. Le produit croisé ou croix est indiqué par sa grandeur plus sa direction et son sens:
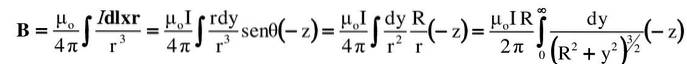
L'intégrale proposée se trouve dans un tableau d'intégrales ou elle est résolue par une substitution trigonométrique appropriée (le lecteur peut vérifier le résultat en utilisant y = Rtg θ):
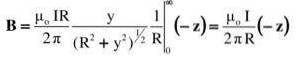
Le résultat est conforme à ce qui était attendu: l'amplitude du champ diminue avec la distance R et augmente proportionnellement avec l'intensité du courant I.
Bien qu'un fil infiniment long soit une idéalisation, l'expression obtenue est une très bonne approximation pour le champ d'un fil long.
Avec la loi de Biot et Savart, il est possible de trouver le champ magnétique d'autres distributions très symétriques, comme une boucle circulaire qui transporte du courant, ou des fils pliés combinant des segments rectilignes et curvilignes..
Bien entendu, pour résoudre analytiquement l'intégrale proposée, le problème doit avoir un haut degré de symétrie. Sinon, l'alternative est de résoudre numériquement l'intégrale.
Les références
- Serway, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. 2ieme volume. Mexique. Éditeurs d'apprentissage Cengage. 367-372.

Personne n'a encore commenté ce post.