
Formule de la loi de Faraday, unités, expériences, exercice,
La Loi de Faraday dans l'électromagnétisme déclare qu'un flux de champ magnétique changeant est capable d'induire un courant électrique dans un circuit fermé.
En 1831, le physicien anglais Michael Faraday a expérimenté des conducteurs en mouvement dans un champ magnétique et des champs magnétiques variables qui passaient à travers des conducteurs fixes..
Faraday s'est rendu compte que s'il variait le flux du champ magnétique dans le temps, il était capable d'établir une tension proportionnelle à cette variation. Si ε est la tension ou la force électromotrice induite (force électromotrice induite) et Φ est le flux de champ magnétique, sous forme mathématique, il peut être exprimé:
| ε | = ΔΦ / Δt
Où le symbole A indique la variation de la quantité et les barres dans la force électromotrice indiquent la valeur absolue de celle-ci. Puisqu'il s'agit d'un circuit fermé, le courant peut circuler dans un sens ou dans l'autre.
Le flux magnétique, produit par un champ magnétique à travers une surface, peut varier de plusieurs façons, par exemple:
-Déplacement d'un barreau magnétique dans une boucle circulaire.
-Augmenter ou diminuer l'intensité du champ magnétique qui traverse la boucle.
-Laisser le champ fixe, mais au moyen d'un mécanisme changer la zone de la boucle.
-Combiner les méthodes ci-dessus.

Index des articles
- 1 Formules et unités
- 1.1 Loi de Lenz
- 2 expériences de Faraday
- 2.1 Variation du flux magnétique par rotation
- 3 Références
Formules et unités
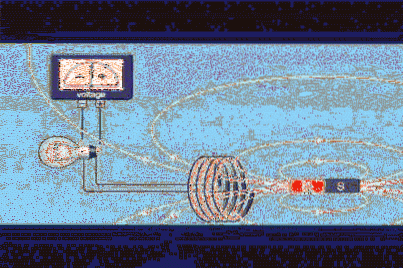
Supposons que vous ayez un circuit fermé de la zone A, comme une boucle circulaire ou un enroulement égal à celui de la figure 1, et que vous ayez un aimant qui produit un champ magnétique B.
Le flux de champ magnétique Φ est une quantité scalaire qui se réfère au nombre de lignes de champ qui traversent la zone A. Sur la figure 1 se trouvent les lignes blanches qui quittent le pôle nord de l'aimant et reviennent par le sud.
L'intensité du champ sera proportionnelle au nombre de lignes par unité de surface, nous pouvons donc voir qu'aux pôles il est très intense. Mais on peut avoir un champ très intense qui ne produit pas de flux dans la boucle, ce que l'on peut réaliser en changeant l'orientation de celui-ci (ou de l'aimant).
Pour prendre en compte le facteur d'orientation, le flux de champ magnétique est défini comme le produit scalaire entre B Oui n, étant n le vecteur normal unitaire à la surface de la boucle et qui indique son orientation:
Φ = B•n A = BA.cosθ
Où θ est l'angle entre B Oui n. Si par exemple B Oui n sont perpendiculaires, le flux de champ magnétique est nul, car dans ce cas le champ est tangent au plan de la boucle et ne peut pas traverser sa surface.
Au lieu de cela oui B Oui n sont parallèles, cela signifie que le champ est perpendiculaire au plan de la boucle et que les lignes le traversent le plus loin possible.
L'unité dans le système international pour F est le weber (W), où 1 W = 1 T.mdeux (lire "tesla par mètre carré").
Loi de Lenz
Sur la figure 1, nous pouvons voir que la polarité de la tension change lorsque l'aimant se déplace. La polarité est établie par la loi de Lenz, qui stipule que la tension induite doit s'opposer à la variation qui la produit.
Si, par exemple, le flux magnétique produit par l'aimant augmente, un courant s'établit dans le conducteur qui circule créant son propre flux, qui s'oppose à cette augmentation..
Si, au contraire, le flux créé par l'aimant diminue, le courant induit circule de telle sorte que son propre flux contrecarre ladite diminution..
Pour prendre en compte ce phénomène, un signe négatif est placé avant la loi de Faraday et il n'est plus nécessaire de placer les barres de valeur absolue:
ε = -ΔΦ / Δt
C'est la loi Faraday-Lenz. Si la variation de débit est infinitésimale, les deltas sont remplacés par des différentiels:
ε = -dΦ / dt
L'équation ci-dessus est valable pour une boucle. Mais si nous avons une bobine de N tours, le résultat est bien meilleur, car la force électromotrice est multipliée N fois:
ε = - N (dΦ / dt)
Expériences de Faraday
Pour que le courant allume l'ampoule à produire, il doit y avoir un mouvement relatif entre l'aimant et la boucle. C'est l'une des façons dont le flux peut varier, car de cette manière, l'intensité du champ traversant la boucle change..
Dès que le mouvement de l'aimant cesse, l'ampoule s'éteint, même si l'aimant reste encore au milieu de la boucle. Ce qu'il faut pour faire circuler le courant qui allume l'ampoule, c'est que le flux de champ varie.
Lorsque le champ magnétique varie avec le temps, nous pouvons l'exprimer comme:
B = B (t).
En gardant la zone A de la boucle constante et en la laissant fixe à un angle constant, qui dans le cas de la figure est de 0 °, alors:


S'il est possible de changer la zone de la boucle, en laissant son orientation fixe et en la plaçant au milieu d'un champ constant, la force électromotrice induite est donnée par:

Une façon d'y parvenir consiste à placer une barre qui glisse sur un rail conducteur à une certaine vitesse, comme illustré dans la figure suivante.

La barre et le rail, plus une ampoule ou une résistance reliée à des fils conducteurs, forment un circuit fermé en forme de boucle rectangulaire..
Lors du glissement de la barre, la longueur X augmente ou diminue, et avec elle la zone de la boucle change, ce qui suffit à créer un flux variable.
Variation du flux magnétique par rotation
Comme nous l'avons déjà dit, si l'angle entre B et la normale de la boucle est amenée à varier, le flux de champ change selon:
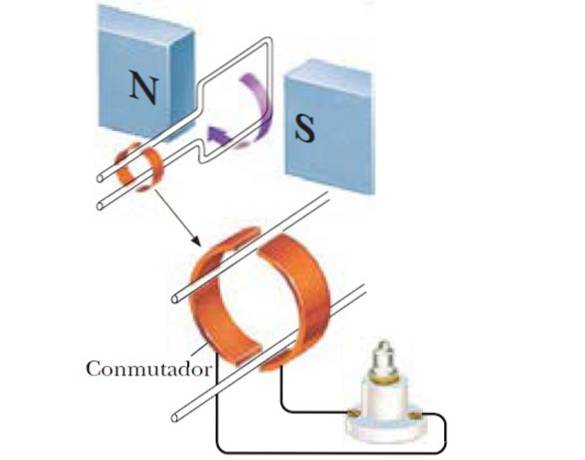

Ainsi, on obtient un générateur sinusoïdal, et si au lieu d'une seule bobine on utilise un nombre N de bobines, la force électromotrice induite est plus grande:


Une bobine circulaire de N tours et de rayon R, tourne avec une fréquence angulaire ω au milieu d'un champ magnétique de magnitude B.Trouvez une expression pour la force électromotrice maximale induite dans la bobine.
Solution
L'expression de la force électromotrice induite par rotation est appliquée lorsque la bobine a N spires, sachant que:
-La surface de la bobine est A = πRdeux
-L'angle θ varie en fonction du temps comme θ = ωt
Il est important de noter que le premier θ = ωt est substitué dans la loi de Faraday et alors est dérivée par rapport au temps:
ε = -NBA (cos θ) '= -NB (πRdeux). [cos (ωt)] '= NBω (πRdeux) sin (ωt)
Puisque la force emf maximale est demandée, elle se produit chaque fois que sin ωt = 1, donc finalement:
εmax = NBω (πRdeux)
Les références
- Figueroa, D. 2005. Série: Physique pour les sciences et l'ingénierie. Volume 6. Electromagnétisme. Edité par Douglas Figueroa (USB).
- Giambattista, A. 2010. Physique. Deuxième édition. Mcgraw Hill.
- Giancoli, D. 2006. Physique: principes avec applications. 6e. Ed. Prentice Hall.
- Resnick, R. 1999. Physique. Volume 2. 3e éd. En espagnol. Compañía Editorial Continental S.A. par C.V.
- Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 2.



Personne n'a encore commenté ce post.