
Explication des lois de Gossen avec des exemples
le Les lois de Gossen, Créées par l'économiste allemand Hermann Gossen (1810-1858), ce sont trois lois économiques pertinentes liées à la diminution de l'utilité marginale, au coût marginal d'acquisition et à la rareté..
Gossen a été le premier à expliquer la loi de l'utilité marginale décroissante, ou la première loi de Gossen, basée sur des observations générales du comportement humain. Cette loi affirme que le montant de la même jouissance diminue continuellement au fur et à mesure que l'on avance sans interruption dans cette jouissance, jusqu'à ce que la satisfaction soit atteinte..

La deuxième loi, la loi d'utilité équi-marginale, explique le comportement des consommateurs lorsqu'ils ont des ressources limitées, mais des besoins illimités..
Le problème fondamental dans une économie est que les besoins humains sont illimités, mais qu'il n'y a pas de ressources adéquates pour satisfaire tous les besoins humains. Par conséquent, un individu rationnel essaie d'optimiser les rares ressources disponibles pour atteindre une satisfaction maximale..
La troisième loi fait référence à la valeur économique des produits, qui résulte d'une pénurie antérieure.
Gossen s'est efforcé de trouver chacune de ces lois dans toutes sortes d'activités économiques.
Index des articles
- 1 Première loi de Gossen
- 1.1 Exemple
- 2 Deuxième loi de Gossen
- 2.1 Exemple
- 3 Troisième loi de Gossen
- 4 Références
Première loi de Gossen
Elle est connue comme la loi de l'utilité marginale décroissante. Il indique que lorsqu'un individu consomme plus d'un produit, l'utilité totale augmente à un rythme décroissant.
Cependant, après un certain stade, l'utilité totale commence également à diminuer et l'utilité marginale devient négative. Cela signifie que l'individu n'a plus besoin du produit..
Autrement dit, le désir d'un individu pour un produit particulier devient saturé lorsqu'il le consomme de plus en plus..
Exemple
Supposons que vous ayez faim et que vous ayez des oranges. Manger la première orange est très utile. L'utilité marginale de la seconde orange est certainement inférieure à celle de la première.
De même, l'utilité marginale de la troisième orange est inférieure à celle de la seconde, et ainsi de suite.
Après un certain stade, l'utilité marginale devient nulle et au-delà de ce stade, elle devient négative. C'est parce qu'il devient rassasié à mesure que de plus en plus d'oranges sont consommées..
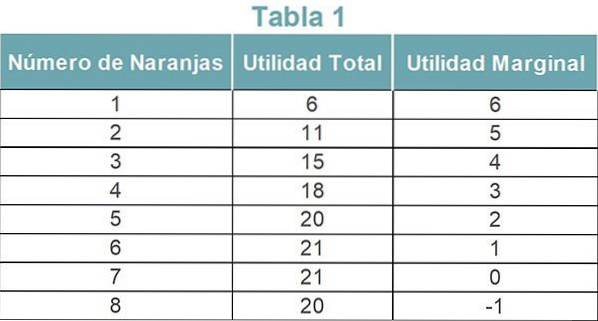
Pour mieux le comprendre, vous pouvez consulter le tableau 1. Les chiffres sont hypothétiques et représentent l'utilité marginale de la consommation d'oranges pour une personne.
Bénéfice total
L'utilité totale est obtenue en additionnant l'utilité marginale de chaque unité consommée d'orange. Selon le tableau 1, l'utilité totale des six premières oranges est de 21 (21 = 6 + 5 + 4 + 3 + 2 + 1).
Utilité marginale
L'utilité marginale de la nième unité du produit est la différence entre l'utilité totale de la nième unité et l'utilité totale de la (n-1) -ième unité du produit. UMn = UTn - UT (n-1) où,
MUn = utilité marginale de la nième unité.
UTn = Bénéfice total de la nième unité.
UT (n-1) = Bénéfice total de l'unité (n-1) -th.
Dans l'exemple du tableau 1, l'utilité marginale de la quatrième orange est CU4 = TU4-TU3 = 18-15 = 3.
La figure suivante détaille les trajectoires des courbes d'utilité totale et d'utilité marginale.
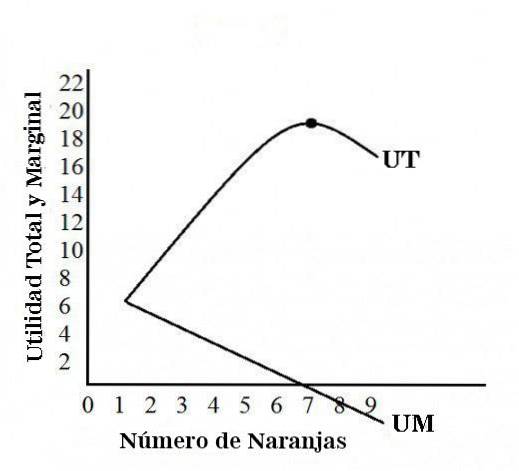
La courbe d'utilité totale augmente initialement et, après un certain stade, commence à diminuer. C'est à ce stade que la courbe d'utilité marginale entre dans la zone négative..
Deuxième loi de Gossen
La deuxième loi dit que chaque personne dépensera son argent sur différents produits, de sorte que le montant de tous les plaisirs soit égal.
De cette manière, Gossen a expliqué que la jouissance maximale serait obtenue à partir d'un niveau de satisfaction uniforme. La deuxième loi de Gossen est connue sous le nom de loi d'utilité équi-marginale.
Supposons qu'une personne possède 200 $. La loi explique comment la personne répartit les 200 $ entre ses différents souhaits pour maximiser sa satisfaction..
Le point auquel la satisfaction du consommateur est la plus élevée avec les ressources données est appelé équilibre du consommateur..
Exemple
Supposons qu'il existe deux produits X et Y. La ressource du consommateur est de 8 $. Le prix unitaire du produit X est de 1 $. Le prix unitaire du produit Y est de 1 $.
Le consommateur dépense ses 8 $ pour acheter le produit X. Le prix unitaire du produit X étant de 1 $, il peut acheter 8 unités.
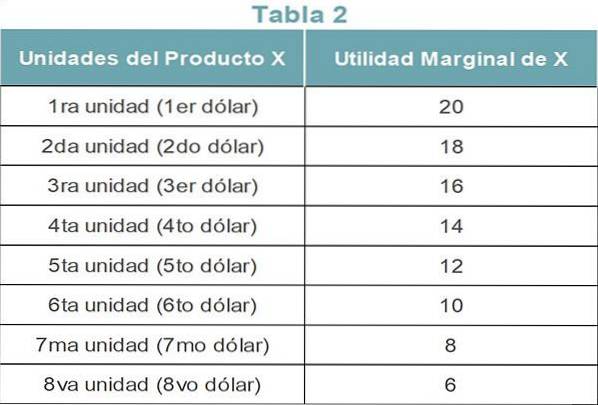
Le tableau 2 montre l'utilité marginale de chaque unité de produit X. Puisque la loi est basée sur le concept d'utilité marginale décroissante, elle diminue avec chaque unité suivante..
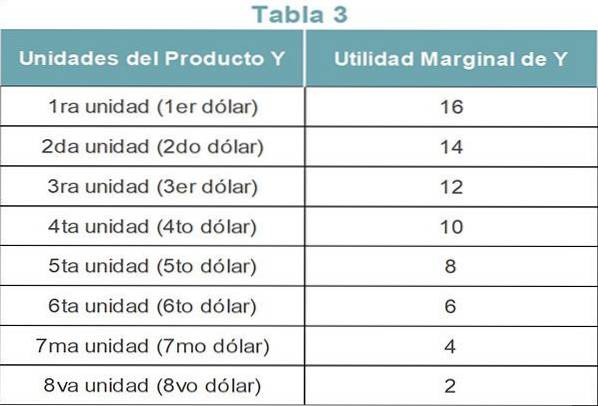
Considérons maintenant que le consommateur dépense ses 8 $ pour acheter le produit Y. Le tableau 3 montre l'utilité marginale de chaque unité de produit Y.
Si le consommateur prévoit de répartir ses 8 $ entre les produits X et Y, le tableau 4 montre comment le consommateur dépense ses revenus sur les deux produits..
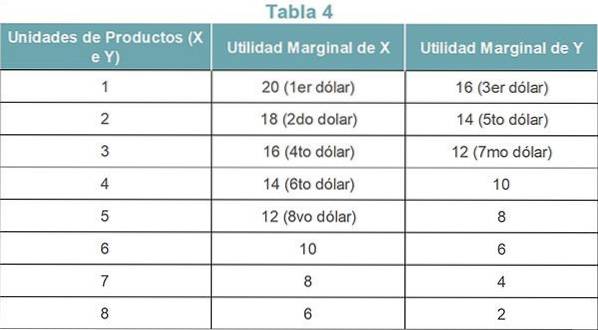
Application de la deuxième loi
Puisque la première unité du produit X donne le profit le plus élevé (20), elle dépense le premier dollar sur X. Le deuxième dollar va également au produit X, car il donne 18, le deuxième plus haut.
La première unité de produit Y et la troisième unité de produit X offrent le même montant de profit. Le consommateur préfère acheter le produit Y, car il a déjà dépensé deux dollars pour le produit X.
De même, le quatrième dollar est dépensé sur X, le cinquième dollar sur Y, le sixième dollar sur X, le septième dollar sur Y et le huitième dollar sur X.
Ainsi, le consommateur achète 5 unités de produit X et 3 unités de produit Y. Autrement dit, 5 unités de produit X et 3 unités de produit Y lui laissent la meilleure quantité d'utilité totale..
Selon la loi de l'utilité équi-marginale, le consommateur est en équilibre à ce point, éprouvant une satisfaction maximale. Pour comprendre cela, l'utilité totale des produits consommés peut être calculée.
Bénéfice total = UTx + UTy = (20 + 18 + 16 + 14 + 12) + (16 + 14 + 12) = 122. Toute autre combinaison de produits laisserait le client avec un bénéfice total inférieur.
La troisième loi de Gossen
Cette loi indique que la rareté est une condition préalable nécessaire à l'existence de la valeur économique. Autrement dit, un produit n'a de valeur que lorsque sa demande dépasse son offre.
En utilisant la logique de Gossen, puisque l'utilité marginale diminue avec la consommation, un produit ne peut avoir une utilité marginale positive ou «valeur» que si l'offre disponible est inférieure à celle nécessaire pour générer la satiété. Sinon, le désir sera rassasié et donc sa valeur sera nulle.
Les arguments de Gossen sur la valeur sont basés sur les deux lois précédentes. Selon lui, la valeur est un terme relatif. Cela dépend de la relation entre l'objet et le sujet.
Au fur et à mesure que la quantité augmente, la valeur de chaque unité ajoutée diminue, jusqu'à ce qu'elle devienne nulle.
Les références
- Kirti Shailes (2018). La première et la deuxième loi de Gossen sur la jouissance humaine. Discussion économique. Tiré de: economicsdiscussion.net.
- Sundaram Ponnusamy (2014). La loi de l'utilité marginale décroissante ou la première loi de Gossen. Owlcation. Tiré de: owlcation.com.
- Sundaram Ponnusamy (2016). La loi de l'utilité équi-marginale ou deuxième loi de Gossen. Owlcation. Tiré de: owlcation.com.
- Concepts économiques (2015). Loi d'utilité marginale décroissante. Tiré de: economicsconcepts.com.
- Wikipédia, l'encyclopédie gratuite (2018). Les lois de Gossen. Tiré de: en.wikipedia.org.



Personne n'a encore commenté ce post.