
Caractéristiques de la ligne perpendiculaire, exemples, exercices
Ongle ligne perpendiculaire C'est celui qui forme un angle de 90 ° par rapport à une autre ligne, courbe ou surface. Notez que lorsque deux lignes sont perpendiculaires et sont sur le même plan, lorsqu'elles se croisent, elles forment quatre angles identiques, chacun de 90 °.
Si l'un des angles n'est pas de 90 °, les lignes sont dites obliques. Les lignes perpendiculaires sont courantes dans la conception, l'architecture et la construction, par exemple le réseau de tuyaux dans l'image suivante.

L'orientation des droites perpendiculaires peut être diverse, comme celles illustrées ci-dessous:
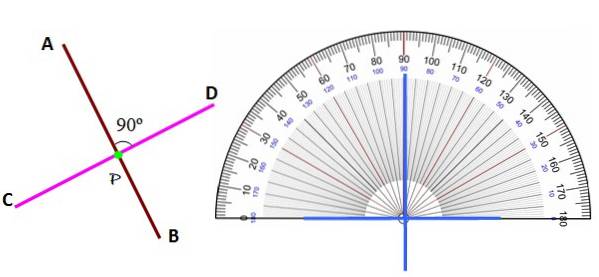
Quelle que soit la position, les lignes perpendiculaires les unes aux autres sont reconnues en identifiant l'angle entre elles à 90 °, à l'aide du rapporteur.
Notez que contrairement aux lignes parallèles dans le plan, qui ne se coupent jamais, les lignes perpendiculaires le font toujours en un point P, appelé le pied d'une des lignes sur l'autre. Par conséquent, deux droites perpendiculaires sont également buvards.
Toute ligne a des perpendiculaires infinies, car simplement en déplaçant le segment AB vers la gauche ou la droite sur le segment CD, nous aurons de nouvelles perpendiculaires avec un autre pied.
Cependant, la perpendiculaire qui passe juste par le milieu d'un segment est appelée bissecteur dudit segment.
Index des articles
- 1 Exemples de droites perpendiculaires
- 1.1 Plus d'exemples de droites perpendiculaires
- 2 exercices
- 2.1 - Exercice 1
- 2.2 - Exercice 2
- 3 Références
Exemples de lignes perpendiculaires
Les lignes perpendiculaires sont courantes dans le paysage urbain. Dans l'image suivante (figure 3), seules quelques-unes des nombreuses lignes perpendiculaires que l'on peut voir sur la façade simple de ce bâtiment et ses éléments tels que portes, conduits, marches et autres ont été mises en évidence:

La bonne chose est que trois lignes perpendiculaires les unes aux autres nous aident à établir l'emplacement des points et des objets dans l'espace. Ce sont les axes de coordonnées identifiés comme Axe X, Axe y Oui Axe z, clairement visible dans le coin d'une pièce rectangulaire comme celle ci-dessous:
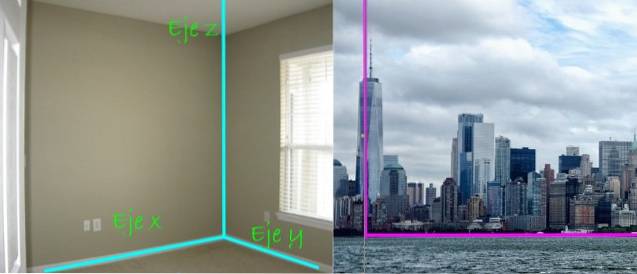
Dans la vue panoramique de la ville, à droite, la perpendicularité entre le gratte-ciel et le sol est également perceptible. Le premier, dirions-nous, se trouve le long du Axe z, tandis que le sol est un plan, qui dans ce cas est le plan xy.
Si le sol constitue l'avion xy, le gratte-ciel est également perpendiculaire à toute avenue ou rue, ce qui garantit sa stabilité, car une structure en pente est instable.
Et dans les rues, partout où il y a des coins rectangulaires, il y a des lignes perpendiculaires. De nombreuses avenues et rues ont un tracé perpendiculaire, pour autant que le terrain et les caractéristiques géographiques le permettent..
Pour exprimer brièvement la perpendicularité entre les lignes, les segments ou les vecteurs, le symbole ⊥ est utilisé. Par exemple, si la ligne L1 est perpendiculaire à la ligne Ldeux, on a écrit:
L1 ⊥ Ldeux
Plus d'exemples de lignes perpendiculaires
- Dans la conception, les lignes perpendiculaires sont très présentes, car de nombreux objets communs sont basés sur des carrés et des rectangles. Ces quadrilatères se caractérisent par des angles internes de 90 °, car leurs côtés sont parallèles deux à deux:
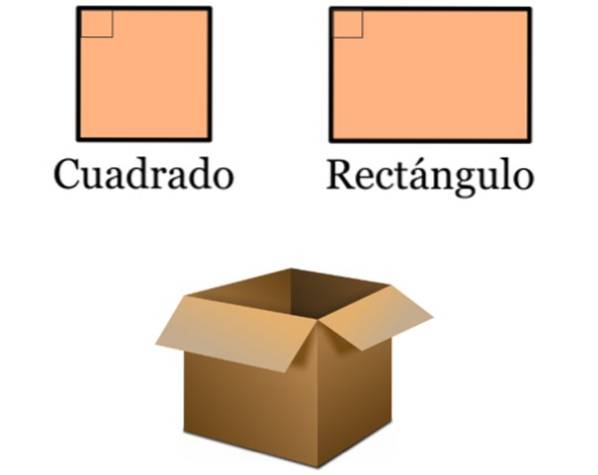
- Les domaines dans lesquels se pratiquent différents sports sont délimités par de nombreux carrés et rectangles. Ceux-ci contiennent à leur tour des lignes perpendiculaires.
- Deux des segments qui composent un triangle rectangle sont perpendiculaires l'un à l'autre. Ceux-ci sont appelés jambes, tandis que la ligne restante est appelée hypoténuse.
- Les lignes du vecteur champ électrique sont perpendiculaires à la surface d'un conducteur en équilibre électrostatique.
- Pour un conducteur chargé, les lignes et surfaces équipotentielles sont toujours perpendiculaires à celles du champ électrique.
- Dans les systèmes de tuyauterie ou de conduits utilisés pour transporter différents types de fluides, tels que le gaz représenté sur la figure 1, les coudes à angle droit sont courants. Ils forment donc des lignes perpendiculaires, c'est le cas d'une chaufferie:

Exercices
- Exercice 1
Tracez deux lignes perpendiculaires à l'aide d'une règle et d'une boussole.
Solution
C'est très simple à faire, en suivant ces étapes:
-La première ligne est dessinée, appelée AB (noir).
-Au-dessus (ou en dessous si vous préférez), marquez le point P, par lequel passera la perpendiculaire. Si P est juste au-dessus (ou en dessous) du milieu de AB, cette perpendiculaire est la bissectrice du segment AB.
-Avec la boussole centrée sur P, tracez un cercle qui coupe AB en deux points, appelés A 'et B' (rouge).
-La boussole est ouverte en A'P, elle est centrée sur A 'et un cercle est dessiné qui passe par P (vert).
-Répétez l'étape précédente, mais ouvrez maintenant la mesure de la longueur du segment B'P (vert). Les deux arcs de circonférence se coupent au point Q sous P et bien sûr au dernier.
-Les points P et Q sont joints à la règle et la ligne perpendiculaire (bleue) est prête.
-Enfin, toutes les constructions auxiliaires doivent être soigneusement effacées, ne laissant que les perpendiculaires..
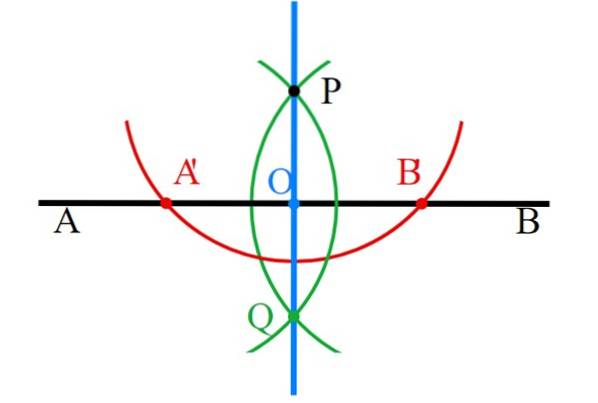
- Exercice 2
Deux lignes L1 et moideux sont perpendiculaires si leurs pentes respectives m1 et Mdeux rencontrer cette relation:
m1 = -1 / mdeux
Étant donné la droite y = 5x - 2, trouvez une ligne perpendiculaire à celle-ci et qui passe par le point (-1, 3).
Solution
-Tout d'abord, trouvez la pente de la ligne perpendiculaire m⊥, comme indiqué dans la déclaration. La pente de la droite d'origine est m = 5, le coefficient qui accompagne «x». Ensuite:
m⊥= -1/5
-Ensuite, l'équation de la ligne perpendiculaire est construite et⊥, en remplaçant la valeur précédemment trouvée:
Oui⊥= -1 / 5x + b
-Ensuite, la valeur de b est déterminée, à l'aide du point donné par l'instruction, (-1,3), puisque la droite perpendiculaire doit la traverser:
y = 3
x = -1
Remplacer:
3 = -1/5 (-1) + b
Résolvez la valeur de b:
b = 3- (1/5) = 14/5
-Enfin l'équation définitive est construite:
Oui⊥= -1 / 5x + 14/5
Les références
- Baldor, A. 2004. Géométrie plane et spatiale. Publications culturelles.
- Clemens, S. 2001. Géométrie avec applications et résolution de problèmes. Addison Wesley.
- Les mathématiques sont amusantes. Lignes perpendiculaires. Récupéré de: mathisfun.com.
- Institut Monterey. Les lignes perpendiculaire. Récupéré de: montereyinstitute.org.
- Wikipédia. Les lignes perpendiculaire. Récupéré de: es.wikipedia.org.



Personne n'a encore commenté ce post.