
Mesures de la tendance centrale pour les formules de données groupées, les exercices

le mesures de tendance central ils indiquent la valeur autour de laquelle se trouvent les données d'une distribution. La plus connue est la moyenne ou moyenne arithmétique, qui consiste à additionner toutes les valeurs et à diviser le résultat par le nombre total de données.
Cependant, si la distribution est constituée d'un grand nombre de valeurs et qu'elles ne sont pas présentées de manière ordonnée, il n'est pas facile d'effectuer les calculs nécessaires pour extraire les informations précieuses qu'elles contiennent..

C'est pourquoi ils sont regroupés en classes ou catégories, pour développer un distribution de fréquences. En effectuant ce classement préalable des données, il est alors plus facile de calculer les mesures de tendance centrale, parmi lesquelles:
-Moitié
-Médian
-mode
-Moyenne géométrique
-Moyenne harmonique
Formules
Voici les formules pour les mesures de tendance centrale pour les données groupées:
Moyenne arithmétique
La moyenne est la plus utilisée pour caractériser les données quantitatives (valeurs numériques), bien qu'elle soit assez sensible aux valeurs extrêmes de la distribution. Il est calculé par:

Avec:
-X: moyenne ou moyenne arithmétique
-Fje: fréquence de classe
-mje: la note de classe
-g: nombre de classes
-n: données totales
Médian
Pour le calculer, il faut trouver l'intervalle qui contient l'observation n / 2 et interpoler pour déterminer la valeur numérique de ladite observation, en utilisant la formule suivante:

Où:
-c: largeur de l'intervalle auquel appartient la médiane
-BM: borne inférieure dudit intervalle
-Fm: nombre d'observations contenues dans l'intervalle
-n / 2: total des données divisé par 2.
-FBM: nombre d'observations avant que de l'intervalle contenant la médiane.
Par conséquent, la médiane est une mesure de la position, c'est-à-dire qu'elle divise l'ensemble de données en deux parties. Ils peuvent également être définis quartiles, déciles Oui centiles, qui divisent la distribution en quatre, dix et cent parties respectivement.
mode
Dans les données regroupées, la classe ou la catégorie qui contient le plus d'observations est recherchée. C'est le classe modale. Une distribution peut avoir deux modes ou plus, auquel cas elle est appelée bimodal Oui multimodal, respectivement.
Vous pouvez également calculer le mode en données groupées en suivant l'équation:

Avec:
-L1: limite inférieure de la classe où se trouve le mode
-Δ1: soustraire entre la fréquence de la classe modale et la fréquence de la classe qui la précède.
-Δdeux: soustraire entre la fréquence de la classe modale et la fréquence de la classe suivante.
-c: largeur de l'intervalle contenant le mode
Moyenne harmonique
La moyenne harmonique est notée H.Lorsque vous avez un ensemble de n valeurs x1, Xdeux, X3…, La moyenne harmonique est l'inverse ou l'inverse de la moyenne arithmétique des inverses des valeurs.
Il est plus facile de le voir à travers la formule:

Et ayant les données groupées disponibles, l'expression devient:

Où:
-H: moyenne harmonique
-Fje: fréquence de classe
-mje: marque de classe
-g: nombre de classes
-N = f1 + Fdeux + F3 +...
Moyenne géométrique
Si elles ont n nombres positifs x1, Xdeux, X3…, Sa moyenne géométrique G est calculée par la nième racine du produit de tous les nombres:

Dans le cas de données groupées, on peut montrer que le logarithme décimal de la moyenne géométrique log G est donné par:

Où:
-G: moyenne géométrique
-Fje: fréquence de classe
-mje: la note de classe
-g: nombre de classes
-N = f1 + Fdeux + F3 +...
Relation entre H, G et X
Il est toujours vrai que:
H ≤ G ≤ X
Définitions les plus utilisées
Les définitions suivantes sont nécessaires pour trouver les valeurs décrites dans les formules ci-dessus:
La fréquence
La fréquence est définie comme le nombre de fois qu'une donnée est répétée.
Rang
C'est la différence entre les valeurs les plus élevées et les plus basses, présentes dans la distribution.
Nombre de cours
Pour savoir dans combien de classes nous regroupons les données, nous utilisons certains critères, par exemple les suivants:

Limites
Les valeurs extrêmes de chaque classe ou intervalle sont appelées limites et chaque classe peut avoir les deux limites bien définies, auquel cas elle a une limite inférieure et une limite supérieure. Ou il peut avoir des limites ouvertes, lorsqu'une plage est donnée, par exemple des valeurs supérieures ou inférieures à un certain nombre.
Marque de classe
Il se compose simplement du milieu de l'intervalle et est calculé en faisant la moyenne de la limite supérieure et de la limite inférieure.
Largeur de l'espace
Les données peuvent être regroupées en classes de taille égale ou différente, c'est la largeur ou la largeur. La première option est la plus utilisée, car elle facilite les calculs, bien que dans certains cas, il soit impératif que les classes aient des largeurs différentes.
La largeur c L'intervalle peut être déterminé par la formule suivante:
c = Gamme / Nc
Oùc est le nombre de classes.
Exercice résolu
Ci-dessous, nous avons une série de mesures de vitesse en km / h, prises avec un radar, qui correspondent à 50 voitures qui ont traversé une rue dans une certaine ville:
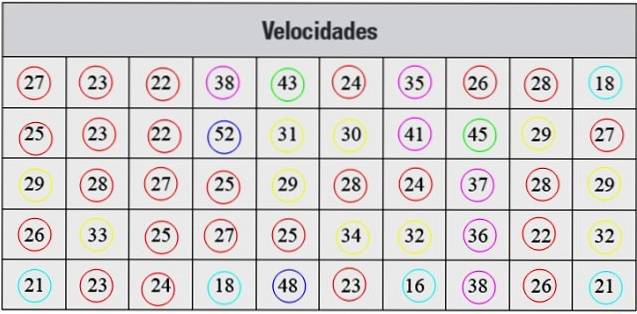
Solution
Les données présentées de cette manière ne sont pas organisées, la première étape est donc de les regrouper en classes.
Étapes pour regrouper les données et construire le tableau
Étape 1
Retrouvez la gamme R:
R = (52 - 16) km / h = 36 km / h
Étape 2
Sélectionnez le nombre de classes Nc, selon les critères donnés. Puisqu'il y a 50 données, nous pouvons choisir Nc = 6.
Étape 3
Calculer la largeur c de l'intervalle:
c = Gamme / Nc = 36/6 = 6
Étape 4
Formez les classes et regroupez les données comme suit: pour la première classe, une valeur légèrement inférieure à la valeur la plus basse présente dans le tableau est choisie comme limite inférieure, puis la valeur de c = 6, précédemment calculée, est ajoutée à cette valeur, donc obtient la limite supérieure de la première classe.
Nous procédons de la même manière pour construire le reste des classes, comme indiqué dans le tableau suivant:
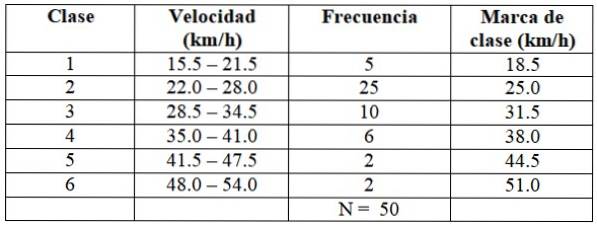
Chaque fréquence correspond à une couleur de la figure 2, de cette manière, il est garanti qu'aucune valeur n'échappe au comptage..
Calcul de la moyenne

X = (5 x 18,5 +25 x 25,0 + 10 x 31,5 + 6 x 38,0 + 2 x 44,5 + 2 x 51,0) ÷ 50 = 29,03 km / h
Calcul de la médiane

La médiane est en classe 2 du tableau, car il y a les 30 premières données de la distribution.
-Largeur de l'intervalle auquel appartient la médiane: c = 6
-Limite inférieure de l'intervalle où la médiane est: BM = 22,0 km / h
-Nombre d'observations que contient l'intervalle fm = 25
-Total des données divisé par 2: 50/2 = 25
-Nombre d'observations qu'il y a avant que de l'intervalle contenant la médiane: fBM = 5
Et l'opération est:
Médiane = 22,0 + [(25-5) ÷ 25] × 6 = 26,80 km / h
Calcul de la mode

La mode est également en classe 2:
-Largeur d'intervalle: c = 6
-Limite inférieure de la classe où se trouve le mode: L1 = 22,0
-Soustrayez entre la fréquence de la classe modale et la fréquence de la classe qui la précède: Δ1 = 25-5 = 20
-Soustrayez entre la fréquence de la classe modale et la fréquence de la classe qui suit: Δdeux = 25 - 10 = 15
Avec ces données, l'opération est:
Mode = 22,0 + [20 ÷ (20 + 15)] x6 = 25,4 km / h
Calcul de la moyenne géométrique
N = f1 + Fdeux + F3 +… = 50
log G = (5 x log 18,5 + 25 x log 25 + 10 x log 31,5 + 6 x log 38 + 2 × log 44,5 + 2 x log 51) / 50 =
log G = 1,44916053
G = 28,13 km / h
Calcul de la moyenne harmonique

1 / H = (1/50) x [(5 / 18,5) + (25/25) + (10 / 31,5) + (6/38) + (2 / 44,5) + (2/51)] = 0,0366
H = 27,32 km / h
Résumé des mesures de la tendance centrale
Les unités des variables sont km / h:
-Moyenne: 29.03
-Médiane: 26,80
-Mode: 25,40
-Moyenne géométrique: 28,13
-Moyenne harmonique: 27,32
Les références
- Berenson, M. 1985. Statistiques de gestion et d'économie. Interamericana S.A.
- Canavos, G. 1988. Probabilité et statistiques: applications et méthodes. Mcgraw Hill.
- Devore, J. 2012. Probabilité et statistiques pour l'ingénierie et la science. 8ème. Édition. Cengage.
- Levin, R. 1988. Statistiques pour les administrateurs. 2ème. Édition. Prentice Hall.
- Spiegel, M. 2009. Statistiques. Série Schaum. 4e Édition. Mcgraw Hill.
- Traitement des données groupées. Récupéré de: itchihuahua.edu.mx.
- Walpole, R. 2007. Probabilité et statistiques pour l'ingénierie et les sciences. Pearson.



Personne n'a encore commenté ce post.