
Caractéristiques du modèle atomique actuel, postulats et scientifiques influents

le modèle atomique actuel est celui qui est basé sur la mécanique quantique, en particulier sur l'équation de Schrödinger, sur le principe d'exclusion de Pauli et une propriété de l'électron appelée tourner ou alors tourner.
C'est le modèle le plus largement accepté et utilisé dans l'étude de la structure des atomes, des molécules et de la réactivité chimique des éléments, en raison de la précision de ses prédictions et de sa relative simplicité..

Ce modèle est l'évolution de plusieurs modèles atomiques précédents, tels que le modèle de Rutherford et le modèle de Bohr - Sommerfeld, considérés comme des modèles classiques ou semi-classiques..
Actuellement, il existe des modèles théoriquement plus complets que le modèle de mécanique quantique de Schrödinger, comme le modèle de Dirac-Jordan, qui intègre la relativité restreinte et est basé sur l'équation d'onde de Dirac. Dans cette équation, le spin, propriété des électrons mentionnée au début, apparaît naturellement.
Il existe également des modèles basés sur la théorie quantique des champs, appliqués en physique des hautes énergies. Ces modèles sont excellents pour prédire la création et l'annihilation des particules fondamentales, le but de ce domaine de la physique..
Il est à noter que les théories les plus sophistiquées convergent vers les mêmes résultats que ceux de l'équation de Schrödinger, en particulier pour les atomes légers..
Index des articles
- 1 Caractéristiques du modèle atomique actuel
- 1.1 Onde - dualité des particules
- 1.2 La taille de l'atome
- 2 Postulats du modèle atomique actuel
- 3 scientifiques influençant le modèle atomique actuel
- 4 Articles d'intérêt
- 5 Références
Caractéristiques du modèle atomique actuel
Dans la vision actuelle de l'atome, basée sur la mécanique quantique non relativiste, le concept d'orbites électroniques dans le style des systèmes planétaires ne correspond pas.
Cependant, l'image la plus répandue de l'atome est toujours celle d'un noyau central positif et de quelques points de charge électrique négative (électrons), tournant sur des orbites parfaitement définies autour du noyau central. Mais malgré ses racines, il ne correspond plus au modèle atomique actuel.
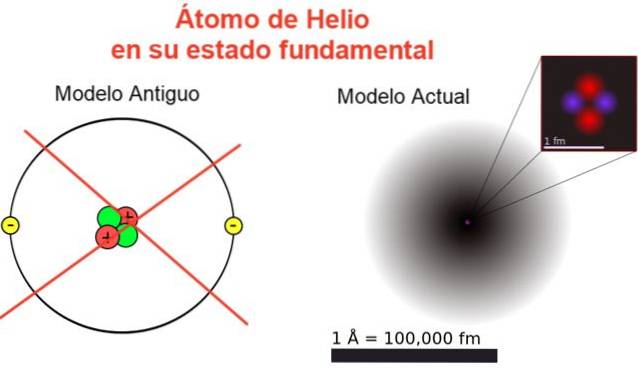
La figure 2 montre l'ancienne image et l'image actuelle d'un atome d'hélium dans son état d'énergie le plus bas (niveau n = 1 et l = 0).
L'image classique est utile pour voir que le noyau contient deux protons et deux neutrons. Garantissant la neutralité de l'atome, il y a deux électrons occupant le même niveau d'énergie.
Le reste est une image loin de la réalité, puisque l'échelle du noyau ne correspond même pas à celle de l'atome: le noyau fait 1/100000 fois la taille de l'atome, mais c'est là que se concentre la masse atomique.
Dualité onde-particule
La mécanique classique établit que chaque particule de matériau a une onde associée, appelée fonction d'onde. C'est le fameux dualité onde-particule par Louis De Broglie.
Dans le modèle atomique actuel, le comportement de l'électron à l'échelle des atomes est en bonne place en forme d'onde, tandis qu'au niveau macroscopique, comme les électrons se déplaçant dans les tubes cathodiques des anciens téléviseurs, le comportement corpusculaire prédomine..
Par contre, avec les photons, c'est l'inverse qui se produit, dans la plupart des phénomènes optiques (au niveau macroscopique) ils ont un comportement fondamentalement ondulatoire. Et quand ils interagissent avec des atomes de matière, ils ont un comportement de particules.
Pour cette raison, les électrons autour du noyau sont dispersés dans des zones appelées orbitales atomiques, dont la forme et l'étendue dépendront du niveau d'énergie des électrons et du moment cinétique.
Tant l'énergie que le moment cinétique de l'électron autour du noyau ont certaines valeurs autorisées, on dit donc qu'ils sont quantifié.
L'équation d'onde de Schrödinger prédit quelles valeurs d'énergie et de moment angulaire sont autorisées, ainsi que la fonction d'onde associée à chaque niveau d'énergie et impulsion..
Le carré mathématique de la fonction d'onde détermine les orbitales, c'est-à-dire les zones autour du noyau où les électrons peuvent être trouvés avec une plus grande probabilité.
La taille de l'atome
Pour avoir une image à l'échelle du modèle atomique actuel, imaginons qu'un atome a un diamètre comme celui d'un terrain de football. Le noyau serait comme une fourmi au centre du champ, mais étonnamment avec 99,9% de la masse atomique.
D'autre part, les électrons seraient comme des joueurs fantomatiques diffusés dans tout le champ, avec une plus grande probabilité d'être trouvés au milieu du terrain..
Il y a quelques alignements ou moyens autorisés pour occuper le champ, qui dépendent de l'énergie des joueurs (les électrons) et de la quantité de «rotation» ou de rotation autour du centre..
Postulats du modèle atomique actuel
1.- L'électron est caractérisé par sa masse m, par son spin s et parce que c'est la particule portant une charge élémentaire négative (-e).
2.- Les électrons ont un double comportement, d'onde-particule simultanée, mais selon leur énergie et l'ampleur du phénomène, l'un peut être plus prépondérant que l'autre..
3.- Les électrons entourent le noyau atomique positif, de manière à garantir la neutralité électrique de l'atome. Par conséquent, le nombre d'électrons est égal au nombre de protons; c'est lui numéro atomique, qui donne les caractéristiques chimiques et physiques de chaque élément.
4.- L'interaction entre les électrons et le noyau est modélisée par le potentiel V (r) Coulomb électrostatique, auquel le terme d'énergie potentielle est incorporé dans l'opérateur hamiltonien.
5.- Le terme d'énergie cinétique dans l'opérateur hamiltonien est un opérateur qui est construit à partir de l'opérateur de moment linéaire, étant le même:
p = - je ħ ∂ / ∂r
Où ħ est la constante de Planck divisée par 2π.
6.- L'opérateur hamiltonien H = (p⋅p)/ 2m - e V (r) agit sur la fonction d'onde électronique Ψ (r).
7.- Lorsque les solutions stationnaires de la fonction d'onde électronique sont recherchées, l'équation de Schrödinger indépendante du temps est utilisée:
H Ψ (r) = E Ψ (r)
Où E représente l'énergie totale de l'électron.
8.- Dans les atomes à plusieurs électrons, l'interaction entre eux n'est pas prise en compte.
9.- En ce qui concerne les atomes de nombreux électrons, les orbitales des électrons les plus externes sont modélisées par le potentiel du noyau protégé par les électrons les plus internes, connu sous le nom de potentiel Debye.
10.- L'équation (7) a une solution pour certaines valeurs d'énergie discrètes, de sorte que le fameux planck quanta, apparaissent naturellement à partir des solutions de l'équation de Schrödinger.
11.- Pour chaque valeur discrète de E il y a une fonction d'onde. Mais certaines solutions sont dégénérées, en fonction de la valeur du moment cinétique L.
12.- La fonction d'onde est le produit d'une fonction radiale, de la fonction azimutale et de la fonction polaire.
13.- Cette fonction d'onde détermine les régions autorisées pour l'électron. Le carré de la fonction d'onde est le densité de probabilité pour trouver l'électron dans une certaine position, vu du centre du noyau atomique.
14.- Le spin n'apparaît pas dans l'équation de Schrödinger, mais il est incorporé dans le modèle atomique par le principe de Pauli:
L'électron est un fermion avec deux états de spin possibles + ½ et -½.
Ainsi, le même état caractérisé par les nombres quantiques n, l, m de l'équation de Schrödinger, peut être occupé par au plus 2 électrons avec des spins opposés. De cette façon, le spin devient le quatrième nombre quantique.
Des scientifiques influents dans le modèle atomique actuel
Cela semble incroyable, mais la plupart des physiciens qui ont contribué au modèle atomique actuel apparaissent sur la même photo. Ils se sont rencontrés lors des célèbres conférences parrainées par Ernest Solvay, chimiste et industriel d'origine belge, devenu célèbre dans le monde de la science..
Ils ont commencé à se tenir en 1911 et ont réuni les plus grands scientifiques du moment, parmi lesquels se trouvaient pratiquement tous ceux qui ont apporté leur contribution au modèle atomique actuel..
La plus célèbre de ces conférences a eu lieu à Bruxelles en 1927 et cette photographie historique y a été prise:


- Peter Debye
- Irving Langmuir
- Martin Knudsen
- Auguste Piccard
- Max Planck
- William Lawrence Bragg
- Émile Henriot
- Paul Ehrenfest
- Marie Curie
- Hendrik Anthony Kramers
- Edouard Herzen
- Hendrik Antoon Lorentz
- Théophile de Donder
- Paul Adrien Maurice Dirac
- Albert Einstein
- Erwin Schrödinger
- Arthur Holly Compton
- Jules-Émile Verschaffelt
- Paul Langevin
- Louis-Victor de Broglie
- Charles-Eugène Guye
- Wolfgang Pauli
- Werner Heisenberg
- Max né
- Charles Thomson Rees Wilson
- Ralph Howard Fowler
- Léon Brillouin
- Niels Bohr
- Owen Williams Richardson
Articles d'intérêt
Modèle atomique de Schrödinger.
Modèle Atomic de Broglie.
Modèle atomique de Chadwick.
Modèle atomique de Heisenberg.
Le modèle atomique de Perrin.
Le modèle atomique de Thomson.
Modèle atomique de Dalton.
Modèle atomique de Dirac Jordan.
Modèle atomique de Démocrite.
Modèle atomique de Leucippe.
Modèle atomique de Bohr.
Les références
- Alonso - Finn. Fondements quantiques et statistiques. Addison Wesley.
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
- Eisberg et Resnick. Physique quantique. Limusa - Wiley.
- Wikipédia. Théorie atomique. Récupéré de: es.wikipedia.com
- Zapata F. Modèle quantique-mécano de l'atome. Récupéré de: lifeder.com



Personne n'a encore commenté ce post.