Formules de moment d'inertie, équations et exemples de calcul

le moment d'inertie d'un corps rigide par rapport à un certain axe de rotation, représente sa résistance au changement de sa vitesse angulaire autour dudit axe. Il est proportionnel à la masse et aussi à l'emplacement de l'axe de rotation, puisque le corps, selon sa géométrie, peut tourner plus facilement autour de certains axes que dans d'autres.

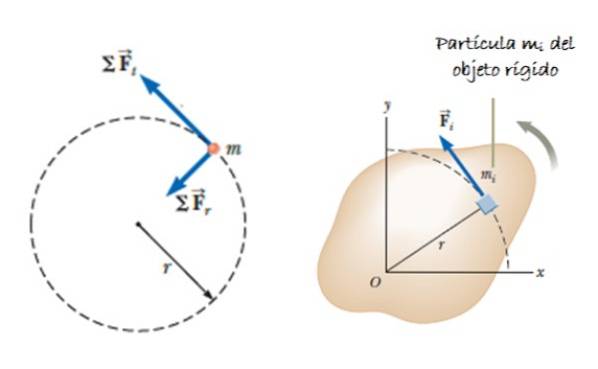
Supposons un grand objet (composé de nombreuses particules) qui peut tourner autour d'un axe. Supposons qu'une force agisse F, appliqué tangentiellement sur la masse élémentaire Δm_je, qui produit un couple ou un moment, donné par τ_rapporter = ∑r_je X F_je. Le vecteur r_je est la position de Δm_je (voir figure 2).

Ce moment est perpendiculaire au plan de rotation (direction +k = sortant du papier). La force et le vecteur de position radiale étant toujours perpendiculaires, le produit croisé reste:

τ_rapporter = ∑ F_je r_je k = ∑ (Δm_je à_je) r_je  k = ∑ Δm_je (à_je r_je ) k

Accélération à_je représente la composante tangentielle de l'accélération, car l'accélération radiale ne contribue pas au couple. En fonction de l'accélération angulaire α, on peut indiquer que:

à_je = α r_je

Par conséquent, le couple net ressemble à ceci:

τ_rapporter = ∑ Δm_je (α r_je^deux) k = (∑ r_je^deux Δm_je) α k

L'accélération angulaire α est la même pour l'objet entier, donc elle n'est pas affectée par l'indice «i» et peut sortir de la sommation, qui est précisément le moment d'inertie de l'objet symbolisé par la lettre I:

I = ∑ r_je^deux Δm_je

C'est le moment d'inertie d'une distribution de masse discrète. Lorsque la distribution est continue, la sommation est remplacée par une intégrale et Δm devient un différentiel de masse dm. L'intégrale est réalisée sur l'ensemble de l'objet:

I = ∫_M(r^deux) dm

Les unités du moment d'inertie dans le système international SI sont le kg x m^deux. C'est une grandeur scalaire et positive, puisqu'elle est le produit d'une masse et du carré d'une distance.

Index des articles

• 1 Exemples de calcul
  • 1.1 Moment d'inertie d'une barre mince par rapport à un axe passant par son centre
  • 1.2 Moment d'inertie d'un disque par rapport à un axe passant par son centre
  • 1.3 Moment d'inertie d'une sphère solide par rapport à un diamètre
  • 1.4 Moment d'inertie d'un cylindre plein par rapport à l'axe axial
  • 1.5 Moment d'inertie d'une feuille rectangulaire par rapport à un axe passant par son centre
  • 1.6 Moment d'inertie d'une feuille carrée par rapport à un axe passant par son centre
• 2 Théorèmes du moment d'inertie
  • 2.1 Théorème de Steiner
  • 2.2 Théorème des axes perpendiculaires
• 3 Exercice résolu
• 4 Références

Exemples de calcul

Un objet étendu, tel qu'une barre, un disque, une sphère ou autre, dont la densité ρ est constante et sachant que la densité est le rapport masse-volume, le différentiel de masse dm s'écrit:

ρ = dm / dV → dm = ρdV

En substituant dans l'intégrale le moment d'inertie, on a:

I = ∫r^deux ρdV = ρ ∫r^deuxdV

Il s'agit d'une expression générale, valable pour un objet tridimensionnel, dont le volume V et position r sont des fonctions des coordonnées spatiales X, Oui Oui z. Notez qu'étant constante, la densité est en dehors de l'intégrale.

La densité ρ On l'appelle aussi densité volumétrique, mais si l'objet est très plat, comme une feuille ou très fin et étroit comme une tige, d'autres formes de densité peuvent être utilisées, voyons:

- Pour une feuille très fine, la densité à utiliser est σ, la densité de surface (masse par unité de surface) et donne est le différentiel de surface.

- Et s'il s'agit d'une barre mince, où seule la longueur est pertinente, la densité de masse linéaire est utilisée λ et un différentiel de longueur, selon l'axe utilisé comme référence.

Dans les exemples suivants, tous les objets sont considérés comme rigides (non déformables) et ont une densité uniforme.

Moment d'inertie d'une barre mince par rapport à un axe passant par son centre

Nous allons calculer ici le moment d'inertie d'une barre mince, rigide et homogène de longueur L et de masse M, par rapport à un axe passant par le milieu.

Tout d'abord, il est nécessaire d'établir un système de coordonnées et de construire une figure avec la géométrie appropriée, comme ceci:

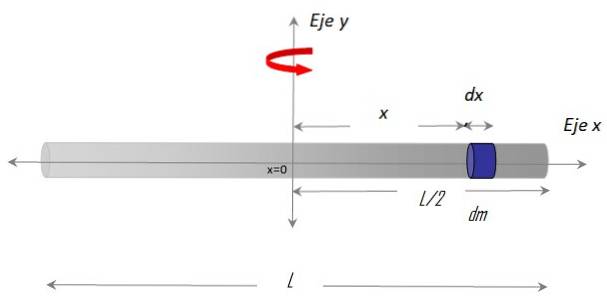
le Axe X le long du bar et le Axe y comme axe de rotation. La procédure d'établissement de l'intégrale nécessite également de choisir un différentiel de masse sur la barre, appelé dm, qui a une longueur différentielle dx et est situé à la position X arbitraire, par rapport au centre x = 0.

Selon la définition de la masse volumique linéaire λ:

λ = M / L

La densité étant uniforme, ce qui est valable pour M et L, elle est également valable pour dm et dx:

λ = dm / dx → dm = λdx.

En revanche, la masse élémentaire est dans la position X, puis en substituant cette géométrie dans la définition, on a une intégrale définie, dont les limites sont les extrémités de la barre selon le repère:

En remplaçant la densité linéaire λ = M / L:

Pour trouver le moment d'inertie de la barre par rapport à un autre axe de rotation, par exemple celui qui passe par l'un de ses extrêmes, vous pouvez utiliser le théorème de Steiner (voir exercice résolu à la fin) ou effectuer un calcul direct similaire à celui montré ici, mais en modifiant la géométrie de manière appropriée.

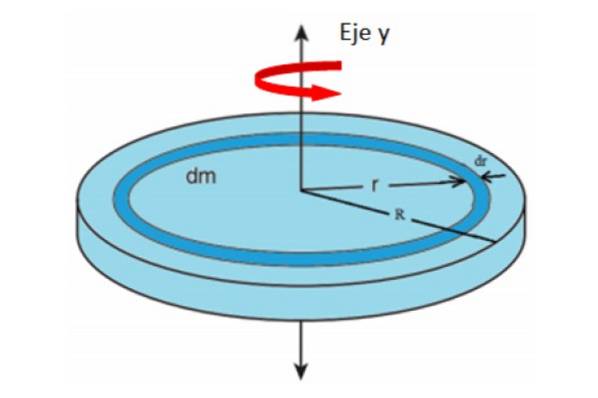
Moment d'inertie d'un disque par rapport à un axe passant par son centre

Un disque très mince d'épaisseur négligeable est une figure plate. Si la masse est uniformément répartie sur toute la surface de la zone A, la densité de masse σ est:

σ = M / Y

Tellement de dm Quoi donne correspondent à la masse et à la surface de la bague différentielle représentée sur la figure. Nous supposerons que l'ensemble de l'assemblage tourne autour de l'axe y.

Vous pouvez imaginer que le disque est composé de nombreux anneaux concentriques de rayon r, chacun avec son moment d'inertie respectif. Ajout des contributions de tous les anneaux jusqu'à atteindre le rayon R, le moment d'inertie total du disque sera.

σ = dm / dA → dm = σdonne

Où M représente la masse entière du disque. La surface d'un disque dépend de son rayon r comme:

A = π.r^deux

Dérivation par rapport à r:

dA / dr = 2 = 2π.r → dA = 2π.rdr

En remplaçant ce qui précède dans la définition de I:

En remplaçant σ = M / (π.R^deux ) restes:

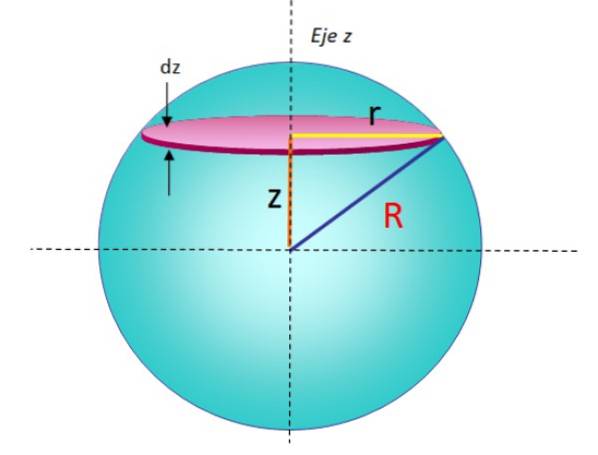
Moment d'inertie d'une sphère solide par rapport à un diamètre

Une sphère de rayon R peut être considérée comme une série de disques empilés les uns sur les autres, où chaque disque de masse infinitésimale dm, radio r et épaisseur dz, a un moment d'inertie donné par:

donné_disque = (½) r^deuxdm

Pour trouver ce différentiel, nous avons simplement pris la formule de la section précédente et remplacé M Oui R pour dm Oui r, respectivement. Un disque comme celui-ci peut être vu dans la géométrie de la figure 5.

En additionnant tous les moments d'inertie infinitésimaux des disques empilés, on obtient le moment d'inertie total de la sphère:

je_sphère = ∫dI_disque

Ce qui équivaut à:

I = ∫_sphère (½) r^deuxdm

Pour résoudre l'intégrale, vous devez exprimer dm correctement. Comme toujours, il est obtenu à partir de la densité:

ρ = M / V = ​​dm / dV → dm = ρ.dV

Le volume d'un disque différentiel est:

dV = aire de la base x hauteur

La hauteur du disque est l'épaisseur dz, tandis que la surface de la base est πr^deux, donc:

dV = πr^deuxdz

Et en remplaçant dans l'intégrale proposée, cela ressemblerait à ceci:

I = ∫_sphère(½) r^deuxdm = ∫ (½) r^deux(ρπr^deuxdz)

Mais avant d'intégrer, il faut observer que r -le rayon du disque- dépend de z et R -le rayon de la sphère-, comme on peut le voir sur la figure 5. En utilisant le théorème de Pythagore:

R^deux = r^deux + z^deux → r^deux = R^deux - z^deux

 Ce qui nous amène à:

I = ∫_sphère(½) ρ r^deux(πr^deuxdz) = ∫_sphère(½) ρ π r⁴dz= ∫_sphère(½) ρ π (R^deux - z^deux)^deux dz

Pour intégrer sur toute la sphère, on note que z varie entre -R et R, donc:

Sachant que ρ = M / V = ​​M / [(4/3) πR³] enfin il est obtenu, après avoir simplifié:

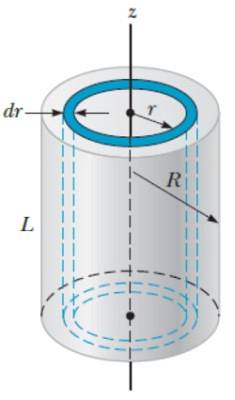
Moment d'inertie d'un cylindre plein par rapport à l'axe axial

Pour cet objet une méthode similaire à celle utilisée pour la sphère est utilisée, mais cette fois c'est plus facile si le cylindre est imaginé formé par des coques cylindriques de rayon r, épaisseur dr et hauteur H, comme si c'étaient les couches d'un oignon.

Le volume dV d'une couche cylindrique est:

dV = 2π.rL.dr

Par conséquent, la masse de la coquille est:

dm = ρ.dV = ρ. 2π.r.L.dr

Cette expression est substituée dans la définition du moment d'inertie:

L'équation ci-dessus indique que le moment d'inertie du cylindre ne dépend pas de sa longueur, mais uniquement de sa masse et de son rayon. Oui L changé, le moment d'inertie autour de l'axe axial resterait le même. Pour cette raison, je du cylindre coïncide avec celui du disque mince précédemment calculé.

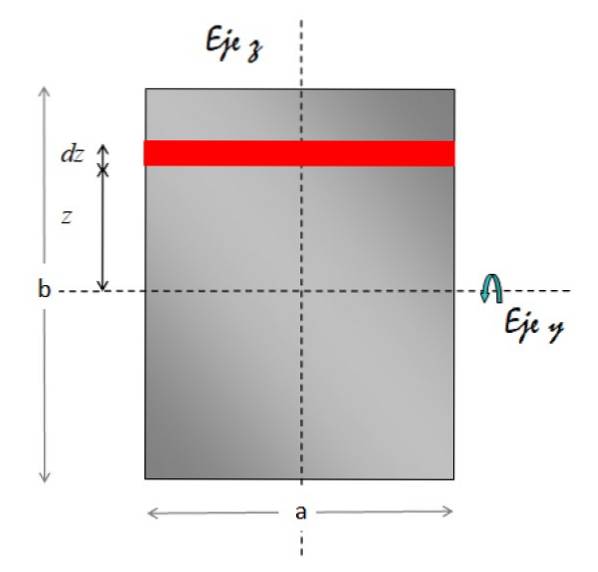
Moment d'inertie d'une feuille rectangulaire par rapport à un axe passant par son centre

le Axe y axe horizontal de rotation. La figure ci-dessous montre la géométrie requise pour réaliser l'intégration:

L'élément de zone marqué en rouge est rectangulaire. Sa surface est base x hauteur, donc:

dA = a.dz

Par conséquent, le différentiel de masse est:

dm = σ.dA = σ. (a.dz)

En ce qui concerne la distance entre l'élément de surface et l'axe de rotation, il est toujours z. Nous substituons tout cela à l'intégrale du moment d'inertie:

Maintenant, la densité de masse surfacique σ est remplacée par:

σ = M / ab

Et cela ressemble vraiment à ceci:

Notez que c'est comme celui avec la barre fine.

Moment d'inertie d'une feuille carrée par rapport à un axe passant par son centre

Pour un carré latéral L, dans l'expression précédente valide pour un rectangle, remplacez simplement la valeur de b pour celui de L:

Théorèmes du moment d'inertie

Il existe deux théorèmes particulièrement utiles pour simplifier le calcul des moments d'inertie autour d'autres axes, qui pourraient autrement être difficiles à trouver en raison du manque de symétrie. Ces théorèmes sont:

Théorème de Steiner

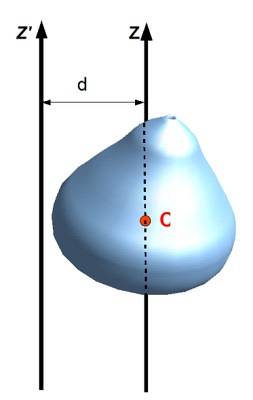
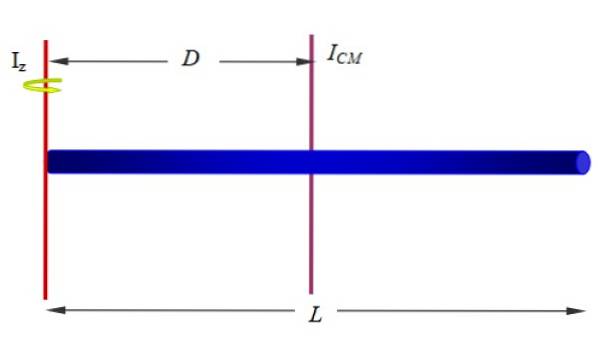
Aussi appelé théorème des axes parallèles, relie le moment d'inertie par rapport à un axe à un autre qui passe par le centre de masse de l'objet, tant que les axes sont parallèles. Pour l'appliquer, il faut connaître la distance D entre les deux axes et bien sûr la masse M de l'objet.

Être je_z le moment d'inertie d'un objet étendu par rapport au axe z, I_CM le moment d'inertie par rapport à un axe passant par le centre de masse (CM) dudit objet, alors il est vrai que:

je_z = Je_CM + MARYLAND^deux

Ou dans la notation de la figure suivante: je_{z '} = Je_z + Maryland^deux

Théorème des axes perpendiculaires

Ce théorème est appliqué aux surfaces planes et va comme ceci: le moment d'inertie d'un objet plan autour d'un axe qui lui est perpendiculaire est la somme des moments d'inertie autour de deux axes perpendiculaires au premier axe:

je_z = Je_X + je_Oui

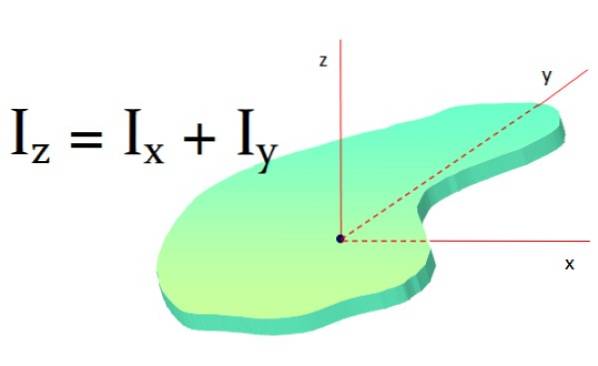
Si l'objet a une symétrie telle que je_X et je_Oui sont égaux, alors il est vrai que:

je_z = 2I_X

Exercice résolu

Trouvez le moment d'inertie de la barre par rapport à un axe qui passe par l'une de ses extrémités, comme indiqué sur la figure 1 (ci-dessous et à droite) et la figure 10.

Solution:

On a déjà le moment d'inertie de la barre autour d'un axe qui passe par son centre géométrique. Puisque la barre est homogène, son centre de masse est à ce point, donc ce sera notre je_CM pour appliquer le théorème de Steiner.

Si la longueur de la barre est L, l'axe z est à une distance D = L / 2, donc:

je_z = Je_CM + MARYLAND^deux= (1/12) ML^deux+M (L / 2)^deux= (1/3) ML^deux

Les références

1. Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill. 313-340
2. Rex, A. 2011. Fondamentaux de la physique. Pearson. 190-200.
3. Théorème de l'axe parallèle. Récupéré de: hyperphysics.phy-astr.gsu.edu.
4. Serway, R. 2018. Physique pour la science et l'ingénierie. Volume 1. Cengage.
5. Université de Séville. Moment d'inertie des solides sphériques. Récupéré de: laplace.us.es.
6. Université de Séville. Moment d'inertie d'un système de particules. Récupéré de: laplace.us.es.
7. Wikipédia. Théorème d'axe parallèle. Récupéré de: en.wikipedia.org