
Angles dans les types de circonférence, propriétés, exercices résolus
Ils s'appellent angles de circonférence ceux dans lesquels certains de ses éléments se trouvent ou se croisent à une circonférence donnée. Parmi eux se trouvent les suivants:
1.- Le angle central, dont le sommet est au centre de la circonférence et ses côtés lui sont sécants, comme on le voit sur l'image suivante:

2.- Le angle inscrit, dont le sommet est sur la circonférence et ses côtés sont sécants ou tangents à la circonférence.
3.- Angle extérieur, dont le sommet est à l'extérieur de la circonférence mais ses côtés sont sécants ou tangents à la circonférence.
4.- Le angle intérieur, avec le sommet à l'intérieur de la circonférence et ses côtés sécants.
Tous ces angles ont certaines relations les uns avec les autres et cela nous conduit à des propriétés importantes entre les angles appartenant à un cercle donné.
Index des articles
- 1 Propriétés
- 1.1 - Angle central
- 1.2 - Angle inscrit
- 1.3 - Angle extérieur
- 1.4 - Angle intérieur
- 2 exercices résolus
- 2.1 - Exercice 1
- 2.2 - Exercice 2
- 3 Références
Propriétés
- Angle central
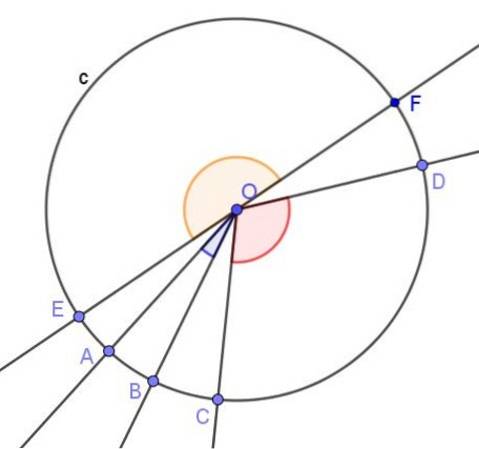
L'angle central est défini comme celui dont le sommet est au centre de la circonférence et ses côtés coupent la circonférence.
La mesure en radians d'un angle central est le quotient entre l'arc sous-jacent, c'est-à-dire l'arc de circonférence entre les côtés de l'angle, et le rayon de la circonférence.
Si la circonférence est unitaire, c'est-à-dire de rayon 1, alors la mesure de l'angle central est la longueur de l'arc, qui correspond au nombre de radians.
Si vous voulez la mesure de l'angle central en degrés, multipliez la mesure en radians par le facteur 180º / π.
Les instruments de mesure d'angle, tels que le rapporteur et le goniomètre, utilisent toujours un angle central et la longueur de l'arc sous-tendu.
Ils sont calibrés en degrés sexagésimaux, ce qui signifie que chaque fois qu'un angle est mesuré avec eux, en arrière-plan ce qui est mesuré est la longueur de l'arc sous-tendu par l'angle central..
Propriété
La mesure d'un angle central en radians est égale à la longueur de l'arc sous-jacent ou intercepteur divisée par la longueur du rayon.
- Angle inscrit
L'angle inscrit d'un cercle est celui qui a son sommet sur la circonférence et ses rayons sont sécants ou tangents à celui-ci..
Ses propriétés sont:
Propriétés
-L'angle inscrit est convexe ou plan.
-Lorsqu'un angle inscrit coupe le même arc que l'angle central, la mesure du premier angle sera la moitié de celle du second..
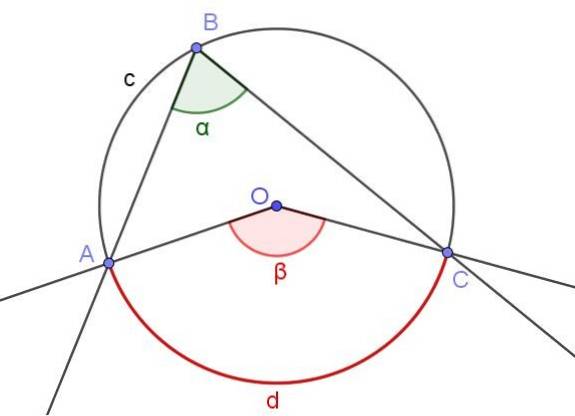
La figure 3 montre deux angles ∠ABC et ∠AOC qui coupent le même arc de circonférence A⌒C.
Si la mesure de l'angle inscrit est α, alors la mesure β de l'angle central est le double de la mesure de l'angle inscrit (β = 2 α) car les deux sous-tendent le même arc de mesure d.
- Angle extérieur
C'est l'angle dont le sommet est à l'extérieur de la circonférence et chacun de ses côtés coupe la circonférence en un ou plusieurs points.
Propriété
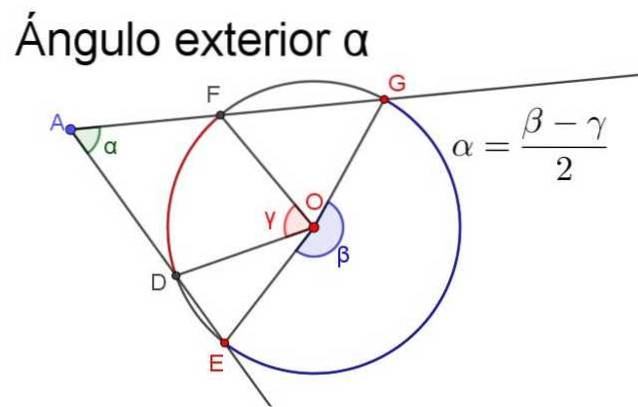
-Sa mesure est égale à la demi-différence (ou différence divisée par 2) des angles centraux qui interceptent les mêmes arcs.
Pour garantir que la mesure est positive, la demi-différence doit toujours être celle du plus grand angle central moins la mesure du plus petit angle central, comme illustré dans la figure suivante.
- Angle intérieur
L'angle intérieur est celui dont le sommet est à l'intérieur de la circonférence et ses côtés coupent la circonférence.
Propriété
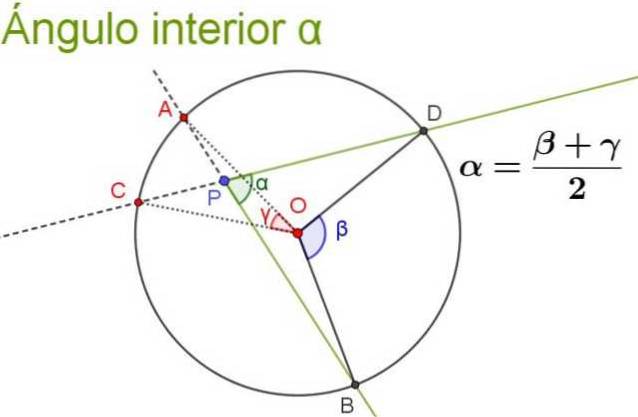
Sa mesure est égale à la demi-somme de l'angle central qui sous-tend le même arc, plus l'angle central qui sous-tend le même arc que son angle d'extension (c'est l'angle intérieur formé par les rayons complémentaires à ceux de l'angle intérieur d'origine ).
La figure suivante illustre et clarifie la propriété de l'angle intérieur.
Exercices résolus
- Exercice 1
Supposons un angle inscrit dans lequel l'un de ses côtés passe par le centre du cercle, comme le montre la figure 6. Le rayon du cercle est OA = 3 cm et l'arc d a une longueur de π / 2 cm. Déterminer la valeur des angles α et β.
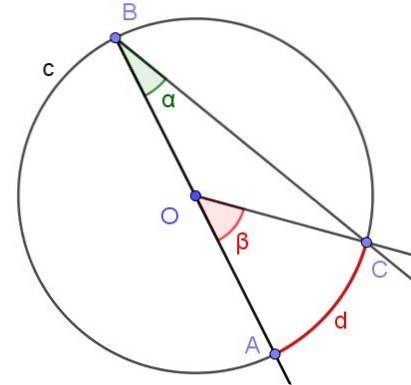
Solution
Dans ce cas, le triangle isocèle COB est formé, puisque [OC] = [OB]. Dans un triangle isocèle, les angles adjacents à la base sont égaux, donc ∠BCO = ∠ABC = α. Par contre ∠COB = 180º - β. En considérant la somme des angles internes du triangle COB, on a:
α + α + (180º - β) = 180º
D'où il résulte que 2 α = β, ou ce qui est équivalent α = β / 2, avec lequel la propriété (3) de la section précédente est confirmée, que la mesure de l'angle inscrit est la moitié de l'angle central, lorsque les deux angles sous-tendre le même accord [AC].
Nous procédons maintenant à la détermination des valeurs numériques: l'angle β est central et sa mesure en radians est le quotient entre l'arc d et le rayon r = OA, donc sa mesure est:
β = d / r = (π / 2 cm) / (3 cm) = π / 6 rad = 30º.
Par contre, il avait déjà été dit que α = β / 2 = (π / 6 rad) / 2 = π / 12 rad = 15º.
- Exercice 2
Sur la figure 7, les angles α1 et βdeux ils ont la même mesure. De plus, l'angle β1 mesure 60º. Déterminer les angles β et α.
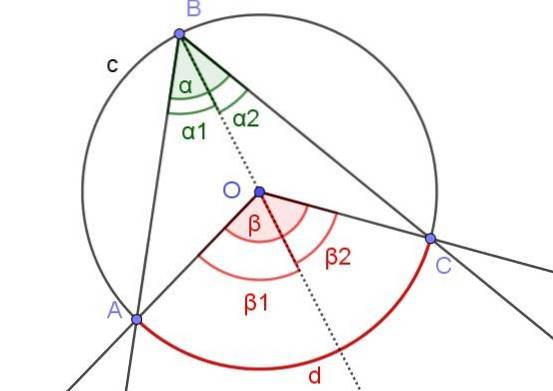
Solution
Dans ce cas, nous avons un angle inscrit ∠ABC dans lequel le centre O de la circonférence est dans l'angle.
En raison de la propriété (3), nous avons αdeux = βdeux / 2 et α1 = β1 /deux. Quoi:
α = α1 + αdeux et β = β1 + βdeux
Par conséquent, il s'ensuit que:
α = α1 + αdeux = β1 / 2 + βdeux / 2 = (β1 + βdeux) / 2 = β / 2.
Autrement dit, selon les propriétés:
α = β / 2
Puisqu'on nous dit que β1 = 60º alors:
α1 = β1 / 2 = 60 ° / 2 = 30 °.
Ils nous disent aussi que α1 = βdeux il s'ensuit donc que:
βdeux = 30º.
L'angle β résulte:
β1 + βdeux = 60 ° + 30 ° = 90 °.
Et puisque α = β / 2, alors:
α = 90 ° / 2 = 45 °.
En conclusion:
β = 90º et α = 45º.
Les références
- Baldor, A. 1973. Géométrie et trigonométrie. Maison d'édition culturelle d'Amérique centrale.
- E. A. 2003. Éléments de géométrie: avec exercices et géométrie de la boussole. Université de Medellin.
- Géométrie 1er ESO. Angles sur la circonférence. Récupéré de: edu.xunta.es.
- Toute la science. Résolution des problèmes d'angles dans la circonférence. Récupéré de: francesphysics.blogspot.com
- Wikipédia. Angle inscrit. Récupéré de: es.wikipedia.com



Personne n'a encore commenté ce post.