
Numéro de Froude comment il est calculé et exemples
le Numéro Froude en hydraulique, il indique la relation qui existe entre les forces d'inertie et les forces gravitationnelles pour un fluide. C'est donc une manière de désigner le quotient suivant:

OùF est la notation du nombre Froude, une quantité sans dimension qui porte ce nom pour honorer le remarquable architecte naval et ingénieur hydraulique britannique William Froude (1810-1879). Froude et son fils ont expérimenté en traînant des draps plats dans l'eau pour estimer la résistance des bateaux aux vagues.

Dans l'action des vagues provoquées par un bateau en navigation ou du courant sur le pilier d'un pont, les forces d'inertie et de gravité sont présentes.
L'indice de Froude est particulièrement important pour caractériser l'écoulement de fluide dans un canal ouvert. Un tuyau ou canal ouvert est un conduit dont la surface supérieure est ouverte sur l'atmosphère. Les exemples abondent dans la nature, sous forme de rivières et de ruisseaux.
Et dans les constructions artificielles, nous avons:
-Gouttières et drains dans les rues et les bâtiments pour conduire l'eau de pluie.
-Fossés pour l'irrigation.
-Décharges et drains.
-Canaux de refroidissement pour machines industrielles.
Ce sont tous des exemples de conduites ouvertes sur l'atmosphère, dans lesquelles le nombre de Froude doit toujours être pris en compte lors de la caractérisation de l'écoulement..
Index des articles
- 1 Calcul du nombre de Froude
- 1.1 Numéro de Froude pour un tuyau ouvert
- 2 types de flux selon le nombre de Froude
- 2.1 Nombre de Froude et nombre de Reynolds
- 3 Exemple travaillé
- 3.1 Solution
- 4 Références
Calcul du nombre de Froude
Le quotient indiqué au début, entre les forces d'inertie et celles de gravité, prend la forme suivante, en fonction des paramètres du fluide:
L'équation précédente ou sa racine carrée est le nombre de Froude:

Numéro de Froude pour un tuyau ouvert
Comme expliqué au début, l'écoulement de l'eau à travers des canaux ouverts sur l'atmosphère est très fréquent. Pour ces cas, le calcul du nombre de Froude est effectué en appliquant la formule suivante:

NF = v / (gyh) ½
Où Ouih est la profondeur hydraulique, v est la vitesse moyenne d'écoulement et g est la valeur de l'accélération due à la gravité. À son tour, la profondeur hydraulique est calculée comme suit:
Ouih = A / T
Dans cette formule, A représente la section transversale nette et T est la largeur de la surface libre du fluide, celle qui est exposée à l'atmosphère, en haut du canal ou du tuyau. Il est valable pour un canal rectangulaire ou suffisamment large et avec une profondeur constante.
Il est important de souligner le fait que, puisque NF est sans dimension, le produit gyh ce doit être le carré d'une vitesse. En effet, on peut montrer que:
cou alorsdeux = gyh
Avec cou alors comme la vitesse de propagation d'une onde de surface, analogue à la vitesse du son dans un fluide. Par conséquent, le nombre de Froude est également analogue au nombre de Mach, largement utilisé pour comparer la vitesse des avions à celle du son..
Types de débit en fonction du nombre de Froude
L'écoulement de fluide dans un canal ouvert est classé en trois régimes, selon la valeur de NF:
-Quand nF < 1, se tiene un movimiento en régimen lento o sous-critique.
-SansF = 1 le flux est nommé flux critique.
-Enfin si vous avez NF > 1 le mouvement est effectué en rapide ou supercritique.
Nombre de Froude et nombre de Reynolds
Nombre de Reynolds NR est une autre grandeur sans dimension qui est très importante dans l'analyse de l'écoulement du fluide, par laquelle on sait quand le fluide a un comportement stratifié et quand est-ce turbulent. Ces concepts s'appliquent à la fois aux écoulements en canalisation fermée et en canal ouvert..
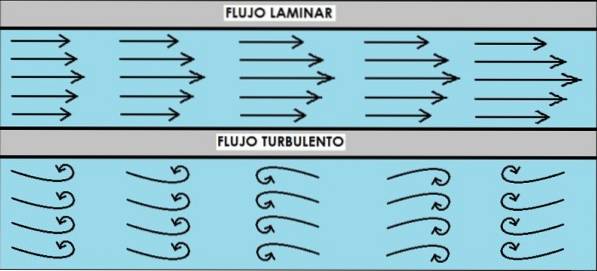
Un écoulement est laminaire lorsque le fluide se déplace de manière fluide et ordonnée dans des couches qui ne se mélangent pas. D'autre part, l'écoulement turbulent se caractérise par être chaotique et désordonné.
Une façon de savoir si un écoulement d'eau est laminaire ou turbulent consiste à injecter un jet d'encre. Si le flux est laminaire, le flux d'encre s'écoule séparément de celui de l'eau, mais s'il s'agit d'un flux turbulent, l'encre se mélange et se dissipe rapidement dans l'eau..

En ce sens, en combinant les effets du nombre de Froude avec ceux du nombre de Reynolds, on a:
-Laminaire sous-critique: NR < 500 y NF < 1
-Sous-critique turbulent: NR > 2000 et NF < 1
-Laminaire supercritique: NR < 500 y NF > 1
-Turbulent supercritique: NR > 2000 et NF > 1
Lorsque les flux se produisent dans les régions de transition, il est plus difficile de les caractériser, en raison de leur instabilité.
Exemple travaillé
Une rivière de 4 m de largeur et 1 m de profondeur a un débit de 3 m3 / s. Déterminer si le flux est sous-critique ou supercritique.
Solution
Pour trouver la valeur de NF il est nécessaire de connaître la vitesse du courant de la rivière. La déclaration nous donne le débit, également appelé débit volumique, qui dépend de la section transversale et de la vitesse v du débit. Il est calculé comme ceci:
Q = A.v
Où Q est le flux, À est l'aire de la section transversale et v est la vitesse. En supposant une section transversale rectangulaire:
A = largeur x profondeur = 4 m x 1 m = 4 mdeux
Alors la vitesse v est:
v = Q / A = 3 m3 / s / 4 mdeux= 0,75 m / s
La profondeur hydraulique dans le cas du tuyau de section rectangulaire coïncide avec la profondeur, par conséquent, en remplaçant les valeurs dans l'équation pour NF, avec Ouih = 1 m Oui g = 9,8 m / sdeux vous avez:
NF = v / (gyh) ½ = 0,75 m / s / (9,8 m / sdeux x 1 m) ½ = 0,24
Puisque NF est inférieur à 1, le flux a un comportement sous-critique, c'est-à-dire lent.
Les références
- Cimbala, C. 2006. Mécanique des fluides, principes fondamentaux et applications. Mc. Colline de Graw.
- Franzini, J. 1999. La mécanique des fluides avec application est en ingénierie. Mc. Colline de Graw.
- Mott, R. 2006. Mécanique des fluides. 4ème. Édition. Éducation Pearson.
- White, F. 2004. Mécanique des fluides. 5e édition. Mc Graw Hill.
- Wikipédia. Numéro Froude. Récupéré de: es.wikipedia.org.



Personne n'a encore commenté ce post.