Les nombres composés sont les nombres entiers qui ont plus de deux diviseurs. Si l'on regarde de plus près, tous les nombres sont au moins divisibles exactement par eux-mêmes et par 1. Ceux qui n'ont que ces deux diviseurs sont appelés nombres premiers, et ceux qui en ont plus sont des composés..
Regardons le nombre 2, qui ne peut être divisé qu'entre 1 et 2. Le nombre 3 a aussi deux diviseurs: 1 et 3. Ils sont donc tous les deux premiers. Regardons maintenant le nombre 12, que nous pouvons diviser exactement par 2, 3, 4, 6 et 12. En ayant 5 diviseurs, 12 est un nombre composé.
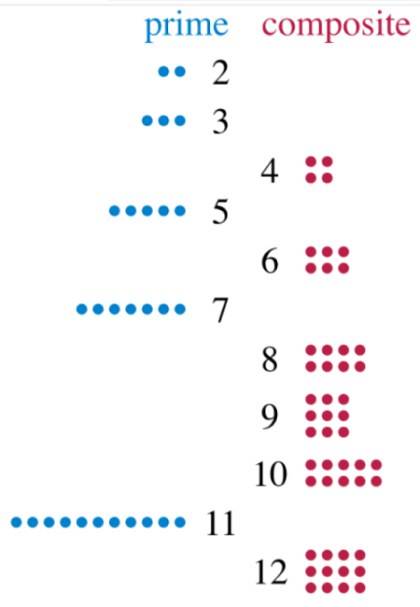
Et que se passe-t-il avec le chiffre 1, celui qui divise tous les autres? Eh bien, ce n'est pas un nombre premier, car il n'a pas deux diviseurs, et il n'est pas composite, donc 1 n'entre dans aucune de ces deux catégories. Mais il y a beaucoup, beaucoup plus de chiffres qui le font..
Les nombres composés peuvent être exprimés comme le produit des nombres premiers, et ce produit, à l'exception de l'ordre des facteurs, est unique pour chaque nombre. Ceci est assuré par le théorème fondamental de l'arithmétique prouvé par le mathématicien grec Euclide (325-365 avant JC).
Revenons au numéro 12, que nous pouvons exprimer de différentes manières. Essayons quelques-uns:
12 = 4 x 3 = 2 x 6 = 12 x 1 = 2deux x 3 = 3 x 2deux = 3 x 2 x 2 = 2 x 2 x 3 = 2 x 3 x 2
Les formes mises en évidence en gras sont des produits de nombres premiers et la seule chose qui change est l'ordre des facteurs, qui, nous le savons, ne modifie pas le produit. Les autres formes, bien que valables pour exprimer 12, ne sont pas uniquement constituées de nombres premiers.
Si nous voulons décomposer un nombre composé en ses facteurs premiers, nous devons le diviser en nombres premiers de telle sorte que la division soit exacte, c'est-à-dire que le reste soit 0.
Cette procédure s'appelle factorisation prime ou décomposition canonique. Les facteurs premiers peuvent être élevés à des exposants positifs.
Nous allons décomposer le nombre 570, en notant qu'il est pair et donc divisible par 2, qui est un nombre premier.
Nous utiliserons une barre oblique pour séparer le nombre à gauche des séparateurs à droite. Les quotients respectifs sont placés sous le nombre au fur et à mesure qu'ils sont obtenus. La décomposition est terminée lorsque le dernier chiffre de la colonne de gauche est 1:
570 │2
285 │
En divisant par 2, le quotient est 285 qui est divisible par 5, un autre nombre premier, se terminant par 5.
570 │2
285 5
57 │
57 est divisible par 3, également un nombre premier, puisque la somme de ses chiffres 5 + 7 = 12 est un multiple de 3.
570 │2
285 5
57 3
19 │
Enfin nous obtenons 19, qui est un nombre premier, dont les diviseurs sont 19 et 1:
570 │2
285 5
57 3
19-19
1 │
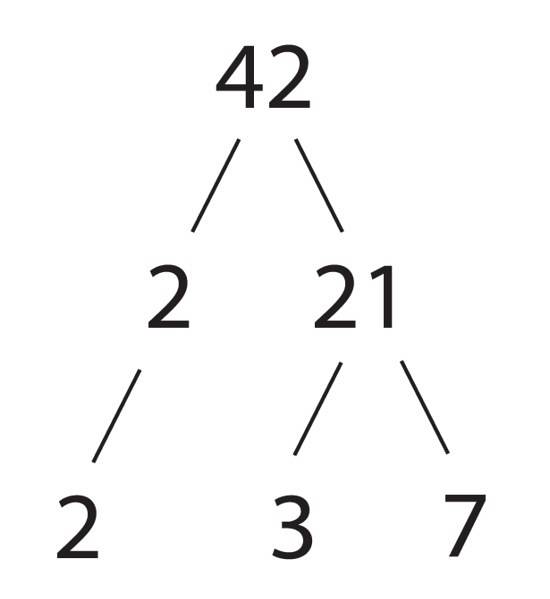
En obtenant 1, nous pouvons déjà exprimer 570 de cette manière:
570 = 2 x 5 x 3 x 19
Et on voit qu'en effet, c'est le produit de 4 nombres premiers.
Dans cet exemple on commence par diviser par 2, mais les mêmes facteurs (dans un autre ordre) auraient été obtenus si on avait commencé par diviser par 5 par exemple.
Pour décomposer un nombre composé en ses facteurs premiers, il est nécessaire de le diviser exactement. Les critères de divisibilité entre nombres premiers sont des règles qui permettent de savoir quand un nombre est divisible par un autre exactement, sans avoir à essayer ou prouver.
Tous les nombres pairs, ceux qui se terminent par 0 ou un nombre pair sont divisibles par 2.
Si la somme des chiffres d'un nombre est un multiple de 3, alors le nombre est également divisible par 3.
Les nombres se terminant par 0 ou 5 sont divisibles par 5.
Un nombre est divisible par 7 si en séparant le dernier chiffre, en le multipliant par 2 et en soustrayant le nombre restant, la valeur résultante est un multiple de 7.
Cette règle semble un peu plus compliquée que les précédentes, mais en réalité ce n'est pas tant que ça, alors regardons un exemple: 98 sera-t-il divisible par 7?
Suivons les instructions: on sépare le dernier chiffre qui est 8, on le multiplie par 2 ce qui donne 16. Le nombre qui reste en séparant le 8 est 9. On soustrait 16 - 9 = 7. Et puisque 7 est un multiple de lui-même , 98 est divisible entre 7.
Si la somme des chiffres en position paire (2, 4, 6…) est soustraite de la somme des chiffres en position impaire (1, 3, 5, 7…) et 0 ou un multiple de 11 est obtenu, le nombre est divisible par 11.
Les premiers multiples de 11 sont facilement identifiables: ils sont 11, 22, 33, 44… 99. Mais attention, 111 n'est pas, au lieu de 110 est.
À titre d'exemple, voyons si 143 est un multiple de 11.
Ce nombre a 3 chiffres, le seul chiffre pair est 4 (le deuxième), les deux chiffres impairs sont 1 et 3 (premier et troisième), et leur somme est 4.
Les deux sommes sont soustraites: 4-4 = 0 et puisque 0 est obtenu, il s'avère que 143 est un multiple de 11.
Le nombre sans le chiffre des unités doit être soustrait de 9 fois ce chiffre. Si le nombre renvoie 0 ou un multiple de 13, le nombre est un multiple de 13.
A titre d'exemple, nous vérifierons que 156 est un multiple de 13. Le chiffre des unités est 6 et le nombre qui reste sans lui est 15. Nous multiplions 6 x 9 = 54 et maintenant nous soustrayons 54 - 15 = 39.
Mais 39 est 3 x 13, donc 56 est un multiple de 13.
Deux ou plusieurs nombres premiers ou composés peuvent être premiers ou co-premiers. Cela signifie que le seul diviseur commun qu'ils ont est 1.
Il y a deux propriétés importantes à retenir en ce qui concerne les coprimes:
-Deux, trois et plus de nombres consécutifs sont toujours premiers l'un par rapport à l'autre.
-La même chose peut être dite pour deux, trois ou plusieurs nombres impairs consécutifs.
Par exemple, 15, 16 et 17 sont des nombres premiers entre eux, de même que 15, 17 et 19.
Un nombre premier a deux diviseurs, le même nombre et 1. Et combien de diviseurs a un nombre composé? Ceux-ci peuvent être des cousins ou des composés.
Soit N un nombre composé exprimé en termes de sa décomposition canonique comme suit:
N = an . bm. cp... rk
Où a, b, c… r sont les facteurs premiers et n, m, p… k les exposants respectifs. Eh bien, le nombre de diviseurs C de N est donné par:
C = (n +1) (m + 1) (p +1)… (k + 1)
Avec C = diviseurs premiers + diviseurs composés + 1
Par exemple 570, qui s'exprime comme ceci:
570 = 2 x 5 x 3 x 19
Tous les facteurs premiers sont augmentés à 1, donc 570 a:
C = (1 + 1) (1 + 1) (1+ 1) (1 +1) = 16 diviseurs
De ces 10 diviseurs nous connaissons déjà: 1, 2, 3, 5, 19 et 570. Il manque 10 diviseurs supplémentaires, qui sont des nombres composés: 6, 10, 15, 30, 38, 57, 95, 114, 190 et 285. On les trouve en observant la décomposition en facteurs premiers et en multipliant également les combinaisons de ces facteurs ensemble..
Décomposez les nombres suivants en facteurs premiers:
a) 98
b) 143
c) 540
d) 3705
98 │2
49 │7
7 │7
1 │
98 = 2 x 7 x 7
143 11
13-13
1 │
143 = 11 x 13
540 │5
108 │2
54 │2
27 │3
9 │3
3 │3
1 │
540 = 5 x 2 x 2 x 3 x 3 x 3 = 5 x 2deux x 33
3705 5
741 │3
247 13
19-19
1 │
3705 = 5 x 3 x 13 x 19
Découvrez si les nombres suivants sont premiers les uns par rapport aux autres:
6, 14, 9
-Les diviseurs de 6 sont: 1, 2, 3, 6
-Quant au 14, il est divisible par: 1, 2, 7, 14
-Enfin 9 a pour diviseurs: 1, 3, 9
Le seul diviseur qu'ils ont en commun est 1, donc ils sont premiers l'un par rapport à l'autre.
Personne n'a encore commenté ce post.