
Les nombres impairs comment les distinguer, des exemples et des exercices
Les nombres impairs sont ces nombres entiers qui ne sont pas divisibles par 2. Cela signifie qu'avec des quantités impaires, vous ne pouvez pas faire de groupes de 2, par exemple, si quelqu'un a 9 bonbons à partager avec un ami et ne veut pas en diviser, on aura 4 bonbons et les 5 autres.
Certains des nombres impairs sont les suivants: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ... Dans cette expression, les ellipses indiquent qu'il y a plus de nombres, à la fois à gauche et à droite.

En regardant de plus près, vous pouvez voir que chaque nombre impair peut être obtenu en ajoutant 2 au nombre précédent. Par exemple, si nous ajoutons 2 à -1 nous obtenons 1, si nous faisons 1 + 2 nous obtenons 3 et ainsi de suite.
On observe également que si les paires sont entrelacées, y compris 0, qui est considéré comme un nombre pair, l'ensemble des entiers est obtenu Z.
C'est pourquoi tout entier naturel impair peut s'écrire sous la forme 2n + 1, où n = 0, ± 1, ± 2, ± 3, ± 4, ± 5…, où le symbole ± signifie que n peut être pris comme positif ou comme négatif.
Dans le cas de nombres plus grands, il peut être reconnu quand il est impair, car il se termine toujours par 1, 3, 5, 7 ou 9. Par exemple, 1571 est impair, tout comme l'entier négatif -152.489.
Index des articles
- 1 Nombres impairs dans la nature et la culture populaire
- 1.1 Nombres premiers
- 2 Opérations sur les nombres impairs
- 2.1 - Sommes et produits
- 2.2 - Pouvoirs
- 3 exercices résolus
- 3.1 - Exercice 1
- 3.2 - Exercice 2
- 3.3 - Exercice 3
- 4 Références
Nombres impairs dans la nature et la culture populaire
Les nombres impairs sont fréquents dans la nature, et parmi eux le nombre 3 a une signification particulière. Regardons quelques exemples:
-Il y a beaucoup de fleurs avec un nombre impair de pétales.
-Nous avons 5 doigts sur chaque main.
-Les humains ont 23 paires de chromosomes.
-Il y a les 3 lois de Newton et les 3 lois de la thermodynamique.
-Les noyaux des atomes qui ont un nombre impair de protons et de neutrons sont moins stables que ceux avec un nombre pair.
-Les sages sont 3.
-Dans les histoires et les nouvelles, le numéro 3 apparaît fréquemment, par exemple des romans comme Les trois Mousquetaires par Alexander Dumas et dans des contes populaires tels que Les trois frères Oui Les Trois Petits Cochons.
-Pour la composition artistique, il y a le soi-disant règle étrange, ce qui établit qu'une composition avec un nombre impair d'éléments est plus attractive qu'une composition avec un nombre pair. Le nombre impair ajoute du dynamisme, tandis qu'un nombre pair ajoute de la stabilité.

-Une stratégie courante pour faire paraître les prix des articles moins chers consiste à les faire finir par 9, disons 2,99 $, 39 $ et ainsi de suite..
-Le nombre 13 est considéré comme malchanceux par certains, tandis que d'autres attribuent des qualités mystiques à 11, les deux nombres impairs..
nombres premiers
Les nombres premiers, ceux qui n'admettent que eux-mêmes et 1 comme diviseur, sont impairs, à l'exception de 2, qui est le seul nombre premier pair.
Il est possible de montrer que tout nombre peut être décomposé en produit de facteurs premiers (y compris les puissances de ceux-ci), et que cette façon d'exprimer le nombre est unique, sauf dans l'ordre des facteurs.
Par exemple, le nombre 45 peut être décomposé en 45 = 33 x 5.
Opérations sur les nombres impairs
Avec des nombres impairs, toutes les opérations arithmétiques sont effectuées, et certaines ont des caractéristiques saillantes.
- Sommes et produits
-La somme de deux nombres impairs donne un nombre pair: 3 + 5 = 8; 11 + 15 = 26; (-10) + (+6) = - 4.
-Lors de l'ajout d'un nombre impair à un nombre pair, le résultat est impair: 7 + 2 = 9; 26+ 9 = 35; (-5) + 12 = 7.
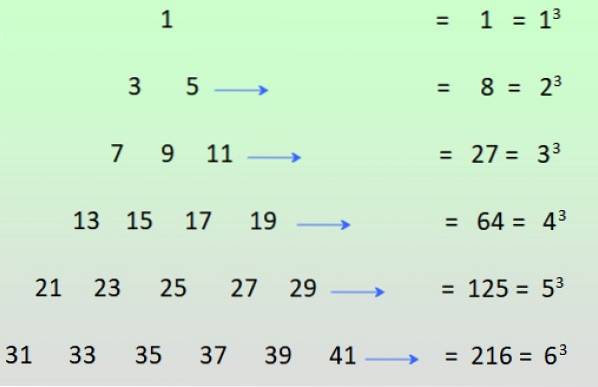
-Si la n premiers nombres naturels, impairs et consécutifs, le résultat est ndeux. Regardons cela un peu plus en détail:
Pour n = 2: 1 + 3 = 4 = 2deux
Pour n = 3: 1 + 3 + 5 = 9 = 3deux
Pour n = 4: 1 + 3 + 5 + 7 = 16 = 4deux
-Lorsqu'un impair est multiplié par un pair, un nombre pair est produit: 7 x 4 = 28; (-3) x 12 = -36.
-La multiplication de deux nombres impairs donne aussi un nombre impair: 3 x 5 = 15; (-5) x (+11) = -55.
- Pouvoirs
-Lorsqu'un nombre positif est élevé à une puissance impaire, il en résulte un nombre positif, par exemple: 33 = 27.
-En élevant un nombre négatif à une puissance impaire, le résultat est négatif: (-2)3= (-2) x (-2) x (-2) = -8.
-Les puissances impaires des entiers positifs peuvent être obtenues si les nombres impairs sont disposés comme indiqué sur la figure et les lignes sont ajoutées:
Exercices résolus
- Exercice 1
Décidez si le résultat de l'opération suivante est pair ou impair:
(53476890083 + 1987628967) x 13567903
Solution
Pour obtenir la réponse, vous n'avez pas besoin de courir pour trouver une calculatrice, mais plutôt d'appliquer les propriétés vues. Regardons les derniers chiffres des addends, qui sont respectivement 3 et 7:
53476890083 + 1987628967
Cela signifie que les addends sont impairs et nous savons déjà que la somme de deux nombres impairs est paire.
Par conséquent, le chiffre qui résulte des parenthèses est pair et nous allons le multiplier par un nombre qui se termine par 3:
13567903
Ce qui signifie que ce nombre est impair.
Dans les propriétés décrites ci-dessus, il a été établi que la multiplication des paires x impaires aboutit à un nombre pair. Par conséquent, l'opération résultante est même.
- Exercice 2
Combien vaut la somme des 5 premiers nombres impairs consécutifs? Et les 50 premiers?
Solution
La somme des 5 premiers nombres impairs consécutifs est:
1 + 3 + 5 + 7 + 9 = 25
Mais si nous voulons ajouter les 50 premiers de cette manière, c'est encombrant, nous allons donc aux propriétés. Ils déclarent que la somme des nombres impairs consécutifs est ndeux. Dans ce cas n = 50 et la somme demandée est:
cinquantedeux = 50 x 50 = 2500.
- Exercice 3
Lorsque vous ajoutez trois nombres impairs consécutifs, vous obtenez 237. Quels sont les nombres?
Solution
Appelons notre premier nombre impair x, et le deuxième et z le troisième, selon l'affirmation il est vrai que:
x + y + z = 237
En langage algébrique, tout nombre impair peut être écrit sous la forme 2n +1. Faisons de notre premier nombre impair:
x = 2n +1
Ajoutons 2 pour obtenir le prochain impair:
y = x + 2 = (2n + 1) + 2 = 2n + 3
Et enfin 2 est ajouté à nouveau pour obtenir le troisième impair:
z = (2n +3) + 2 = 2n + 5
Tout cela s'additionne:
2n + 1 + 2n + 3 + 2n + 5 = 237
6n + 9 = 237
Ce qui aboutit à une équation linéaire simple, dont la solution est:
n = 38
Et maintenant, avec la valeur n = 38, il y a les trois nombres demandés:
x = (2 × 38) + 1 = 77
Les éléments suivants sont donc impairs consécutifs:
y = 79
z = 81
Et le lecteur peut facilement vérifier que la somme des trois est de 237.
Les références
- Baldor, A. 1986. Arithmétique. Éditions et distributions du Codex.
- Barrios, L. Nombres impairs et puissances des nombres naturels. Récupéré de: sinewton.org.
- Brillant. Nombres pairs et impairs. Récupéré de: brilliant.org.
- Mathématiques 18. Opérations avec des nombres impairs. Récupéré de: matematicas18.com.
- Wikipédia. Nombres pairs et impairs. Récupéré de: es.wikipedia.org.


Personne n'a encore commenté ce post.