
Concept de population statistique, types, exemples

La population statistique C'est l'ensemble collectif ou complet d'éléments ayant des caractéristiques communes et que vous souhaitez étudier. Ces éléments peuvent être des personnes, des êtres vivants, des objets inanimés, des événements, des attitudes envers un événement et diverses entreprises..
Des exemples de populations sont les habitants d'un pays ou d'une ville entière, les articles produits par une usine après une journée ou le nombre d'étoiles dans la Voie lactée. De même, toutes les notes obtenues par les étudiants d'une université à la fin du trimestre peuvent être classées en population statistique.
Le chercheur est celui qui décide quelles sont les caractéristiques d'intérêt de la population à étudier. Pour cette raison, l'éventail des possibilités étant si large, les populations sont classées selon certaines caractéristiques exceptionnelles, telles que leur taille..
Cela détermine la manière la plus courante de classer les populations statistiques, de sorte que les populations, en général, sont dites infinies ou finies. Cependant, il existe également d'autres attributs distinctifs, toujours du point de vue de la recherche à mener..
Ces attributs sont définis à l'avance pour s'assurer qu'ils satisfont aux exigences de l'étude et en même temps aident le chercheur à donner à la population le traitement approprié..
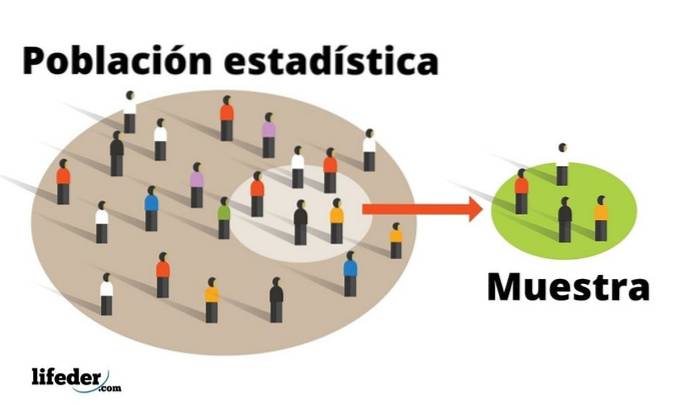
Les populations sont généralement étudiées à travers un échantillon soigneusement sélectionné: il s'agit d'un sous-ensemble représentatif, dont la plus petite taille facilite la gestion. Par extension, les caractéristiques de l'échantillon correspondent à celles de la population dans une marge étroite, que le chercheur établit à sa convenance à l'aide de techniques statistiques..
Types de populations statistiques
En principe, il peut y avoir autant de types de populations statistiques que de caractéristiques à inclure dans leur définition, mais il existe certains critères que la plupart des chercheurs utilisent pour les classer et qui sont universellement applicables..
Il convient également de noter que certaines populations correspondent parfaitement à plus d'une catégorie répertoriée ci-dessous:
Populations infinies
Ce sont des populations théoriques, car elles contiennent une quantité infinie d'éléments. Cependant, certaines populations ont tellement d'éléments qu'elles sont en pratique considérées comme infinies car le total est très difficile à déterminer..
Exemples
-L'ensemble des nombres réels.
-Nombre d'atomes d'oxygène dans l'air dans une pièce.
Populations finies

Ils ont un nombre limité de composants, et leur nombre peut être assez grand ou, au contraire, petit.
Exemple
-Le nombre d'employés dans une entreprise.
-Nombre total d'étudiants dans un pays.
Populations réelles
Il fait référence à un groupe d'éléments dont l'existence est matérielle ou encore à des observations concrètes sur un événement.
Exemples
-Le nombre total de rorquals bleus qui existent.
-L'attitude des consommateurs envers un nouveau produit sur le marché.
Populations hypothétiques
Dans cette catégorie se trouvent des observations sur des événements potentiels et des caractéristiques psychologiques.
Exemple
-Les niveaux d'anxiété d'un groupe de personnes avant la possibilité d'une catastrophe.
Des populations stables
Ce sont des populations dont les caractéristiques sont maintenues dans le temps et dans l'espace, ou ne varient pas de manière significative.
Exemple
-La période de rotation des planètes.
Populations instables
De leur côté, les populations instables présentent une ou plusieurs caractéristiques variables, à la fois dans le temps et dans l'espace..
Exemple

-L'ensemble des personnes dans une ville qui consomme une certaine marque de soda est un exemple de population instable, car les préférences peuvent changer à court terme, si un autre produit avec des caractéristiques plus frappantes apparaît (une marque concurrente qui est en vente ou qui est présenté avec une nouvelle couleur ou saveur ...).
Populations dépendantes
Ils sont liés à une ou plusieurs caractéristiques et peuvent donc varier lorsqu'ils changent, totalement ou partiellement..
Exemple
-Ventes de produits avec des populations qui dépendent, entre autres facteurs, de l'investissement réalisé en publicité.
Populations binomiales
Dans cette population, nous cherchons à déterminer la présence ou l'absence d'une certaine caractéristique.
Exemple
-Dans les études sur la chimie de l'eau minérale destinée à la consommation humaine, il est courant d'indiquer la présence de certains composés, tels que le chlorure de sodium ou le carbonate de calcium.
Populations polynomiales
Dans les populations polynomiales, il est prévu d'effectuer la mesure d'un ensemble de caractéristiques.
Exemple

-Âge, taille et poids des élèves dans une école de base.
Populations aléatoires
Dans ces populations, il y a des changements dus au hasard ou à des circonstances indépendantes de la volonté humaine.
Exemple
-Il existe des procédés industriels dans lesquels des variations imprévues affectent la qualité des produits finis. Si pendant une semaine d'orages il y avait des pannes de courant, qui ont affecté une usine de gobelets en carton, la production de cette semaine peut ne pas être de la même qualité que la production régulière.
Exemples de population statistique
Vous trouverez ci-dessous une liste illustrative des populations des différents types qui peuvent être présentes dans de nombreuses régions. Il est important de souligner à nouveau qu'une même population peut appartenir à plus d'un des types décrits, car elle a des caractéristiques communes avec eux..
- La population totale de chats d'un pays (population réelle et infinie).

- Molécules d'eau dans l'océan Atlantique (c'est une population réelle et infinie, car elle contient une telle quantité d'éléments qu'il est en pratique impossible de les totaliser).
- Tous les virus présents sur Terre (population réelle et infinie).
- Nombre de naissances prématurées au cours du trimestre suivant (population hypothétique, puisque les naissances n'ont pas encore eu lieu, et il est également fini).
- Nombre d'animaux touchés lors de la prochaine saison sèche par d'éventuels incendies de forêt (population hypothétique et finie).
- Nombre d'étoiles au cœur de la Voie lactée (population finie et stable, car le nombre d'étoiles reste constant pendant longtemps et est également réel).
-L'ensemble de tous les nombres premiers (population infinie, stable et réelle).
- Taux de cholestérol dans la population des pays de l'Union européenne (population finie, dépendante, réelle, instable).
- Nombre de survivants en cas d'éruption du Vésuve (population hypothétique, finie, instable).
Les références
- Glossaire des concepts statistiques. Récupéré de: psi.uba.ar.
- Statistiques par Jim. Populations, paramètres et échantillons dans les statistiques inférentielles. Récupéré de: statisticsbyjim.com.



Personne n'a encore commenté ce post.