La presserelatif sur est celui qui est mesuré par rapport à une certaine valeur ou données, qui est généralement la pression atmosphérique au niveau de la mer (pression atmosphérique standard). Ceci est approprié car une grande partie des mesures de pression sont effectuées sous les couches gazeuses qui composent l'atmosphère, qui exercent leur propre pression..
Au lieu de cela, la pression absolue est mesurée par rapport à un vide total, dans lequel il n'y a pas de molécules en interaction. Dans un récipient dans lequel un vide a été effectué, il n'y a pas de particules agissant de l'intérieur sur les parois ou sur les objets à l'intérieur..
Les pressions mesurées peuvent être supérieures ou inférieures à la pression atmosphérique. Dans le premier cas, on parle de la pression manométrique et dans la seconde des pression de vide.
Normalement, les pressions mesurées quotidiennement dans les pneus et la pression artérielle sont des pressions relatives, tandis que lorsque la pression atmosphérique est mesurée à l'aide d'un baromètre, il s'agit d'une pression absolue..
Index des articles
Étant la pression relative, la différence entre la pression absolue Pabdos et pression atmosphérique Pau m, c'est une pression différentielle ou une différence de pression. À la pression relative Prel Il est connu en anglais sous le nom de pression manométrique Pg et est donnée par la relation:
Pabdos = Pau m + Pg
Prel = Pabdos - Pau m
Pour la pression, le pascal est utilisé comme unité de mesure du Système international d'unités, qu'il s'agisse d'une pression absolue ou d'une pression relative..
Le pascal est égal à la force exercée par 1 newton sur une surface de 1 mdeux, mais d'autres unités sont fréquemment utilisées, telles que des millimètres de mercure, d'eau, des unités anglo-saxonnes telles que psi et d'autres.
Si la pression absolue en un point et la pression atmosphérique standard sont connues, la pression relative est la soustraction entre les deux.
Par exemple, supposons que la pression absolue dans un certain système soit de 305 kPa. Sachant que la pression atmosphérique standard est de 101,3 kPa, la pression relative est:
Pg = Pabdos - Pau m = 305 à 101,3 kPa = 203,7 kPa
Le kPa ou kilopascal est mille fois supérieur à un pascal. Il est utilisé plus fréquemment, car les valeurs de pression sont de l'ordre de milliers de pascals. Le poids d'une pomme est d'environ 1 newton et un pascal est égal à cette force répartie sur un carré de 1 mètre de côté. D'autres multiples sont également utilisés tels que mégapascal (1 MPa = 1 x 106 Pa) ou le gigapascal (1 GPa = 1x 109 Pennsylvanie).
La pression dans l'exemple est manométrique, car elle est supérieure à la pression atmosphérique, mais il y a des pressions absolues en dessous. Par exemple, si un gaz dans un conteneur a une pression absolue de 50 kPa, sa pression relative est une pression de vide qui produit une aspiration:
Pg = Pabdos - Pau m = 50 à 101,3 kPa = -51,3 kPa
Dans ces exemples, la pression atmosphérique standard a été utilisée, qui est la pression au niveau de la mer. Mais si une plus grande précision est requise dans le calcul, la pression atmosphérique locale peut être utilisée, qui peut différer de 101,3 kPa, car elle dépend de l'altitude et d'autres conditions géographiques..
Dans les textes, les pressions données sont généralement relatives, et s'il est nécessaire de travailler avec des pressions absolues, elles se distinguent par l'utilisation d'indices pour éviter toute confusion..
À chaque point à l'intérieur d'un fluide comme l'eau, il y a une pression. En supposant que l'eau est incompressible, alors sa densité reste constante et la pression varie verticalement.
Il peut être vérifié en prenant une petite portion de liquide sous la forme d'un disque épais mourir qui est au repos au milieu de la masse liquide.
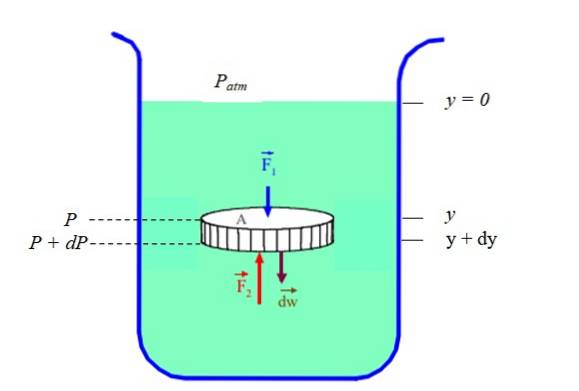
Les forces sur les bords circulaires du disque s'annulent par paires, mais pas les forces exercées par la masse de fluide au-dessus et au-dessous du disque: F1 Oui Fdeux. De plus, il faut tenir compte du poids du disque fluide dW dans la deuxième loi de Newton:
∑FOui = Fdeux - F1 - W = 0
Ces forces peuvent être exprimées en termes de pression, qui est la force perpendiculaire par unité de surface. De cette façon, nous avons la pression P, produite par la force F1:
F1 = P. A
Où A est la zone circulaire du disque. De même:
Fdeux = (P + dP). À
Avec P + dP la pression en profondeur y + dy. Le poids est dW = dm. g:
(P + dP). A - P. A - dm. g = 0
La densité du fluide est ρ = dm / dV, dV étant le volume du disque fluide, donné par A.dy. De cette manière:
(P + dP). A - P. A - ρA.dy .g = 0
L'équation obtenue est simplifiée à:
dP - ρgdy = 0 → dP = ρgdy
Intégrer les deux côtés de et1 jusqu'à etdeux:
= Pdeux - P1 = ρg (etdeux - Oui1)
Le terme Pdeux - P1 c'est une différence de pression ou une pression différentielle. Si nous voulons connaître la pression au point de coordonnée verticale y, nous faisons Oui1 = 0, Ouideux = et Oui Pou alors = Pau m. Avec cela, nous aurons la pression relative à ladite profondeur, qui ne dépend que de la profondeur et:
Pdeux - Pau m = ρgy ⇒ Prel = ρgy
Nous avons tous ressenti la pression de plonger dans une piscine ou dans la mer. Quelle est la pression relative ressentie lors de l'immersion dans une piscine d'eau douce à une profondeur de 5 mètres? En utilisant l'expression précédente, et sachant que la densité de l'eau douce est de 1000 kg / m3, avec g = 9,81 m / sdeux la pression relative est:
Prel = ρgy = 1000 x 9,81 x 5 Pa = 49050 Pa.
Les pneus des véhicules sont généralement à une pression de 32 psi. Il s'agit d'une jauge ou d'une pression relative en livres par pouce carré, l'unité utilisée dans les pays anglophones. De nombreuses jauges sont étalonnées dans ces unités. 32 psi équivaut à 220632 Pa ou 220 kPa.
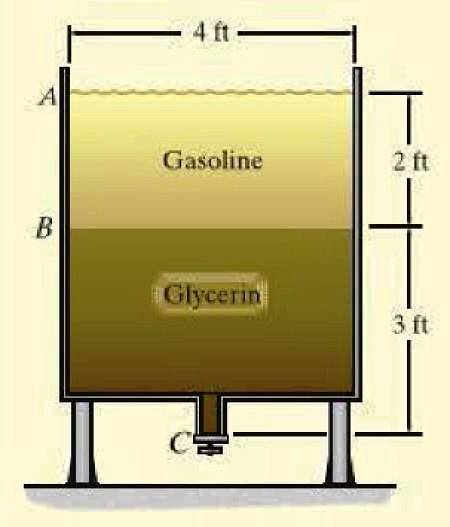
Un réservoir contient de l'essence et de la glycérine, deux liquides non miscibles (ils ne se mélangent pas) aux hauteurs indiquées. Quelle est la pression manométrique au fond du réservoir? Les poids spécifiques, désignés par la lettre grecque γ, de chaque fluide sont attachés:
γgaz = 45,3 lb / pi3
γgly = 78,7 lb / pi3
La gravité spécifique γ d'un fluide est le produit de sa densité et de l'accélération de la gravité, donc l'équation de la pression relative peut être exprimée comme suit:
Prel = γ.y
La pression relative au fond du réservoir est due à la fois au poids de la colonne de glycérine et à celui de l'essence et est indépendante de la forme du réservoir:
Prel = γgaz . OuiUN B + γgly . Ouiavant JC = (45,3 x 2 + 78,7 x 3) lb / pideux = 326,7 lb / pideux
Personne n'a encore commenté ce post.