
Caractéristiques des procédés polytropiques, applications et exemples
UNE procédé polytropique est un processus thermodynamique qui se produit lorsque la relation entre la pression P et le volume V donné par P.Vn il reste constant. L'exposant n est un nombre réel, généralement compris entre zéro et l'infini, mais dans certains cas il peut être négatif.
La valeur de n reçoit le nom de indice de polytropie et il est important de souligner que lors d'un processus thermodynamique polytropique ledit indice doit maintenir une valeur fixe, sinon le processus ne sera pas considéré comme polytropique.

Index des articles
- 1 Caractéristiques des processus polytropiques
- 2 applications
- 2.1 Travaux sur des processus polytropiques pour différentes valeurs de n
- 3 Exemples de procédés polytropiques
- 3.1 - Exemple 1
- 3.2 - Exemple 2
- 4 Références
Caractéristiques des processus polytropiques
Certains cas caractéristiques de processus polytropiques sont:
- Le processus isotherme (à température constante T), dans lequel l'exposant est n = 1.
- Un processus isobare (à pression constante P), dans ce cas n = 0.
- Le processus isochore (à volume constant V), pour lequel n = + ∞.
- Processus adiabatiques (à entropie S constante), dans lesquels l'exposant est n = γ, où γ est la constante adiabatique. Cette constante est le quotient entre la capacité thermique à pression constante Cp divisée par la capacité thermique à volume constant Cv:
γ = Cp / Cv
- Tout autre processus thermodynamique qui ne fait pas partie des cas précédents. mais cela est conforme P.Vn = ctte à indice polytropique réel et constant n ce sera aussi un processus polytropique.
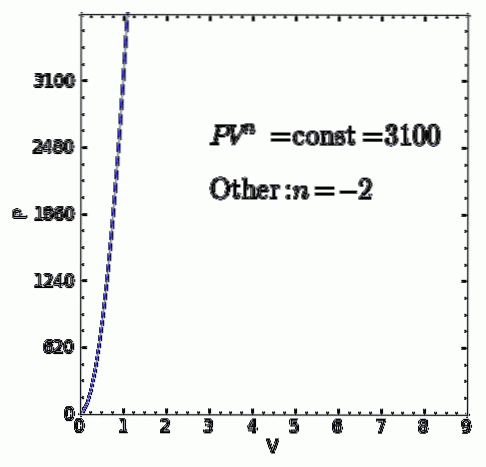
Applications
L'une des principales applications de l'équation polytropique est de calculer le travail effectué par un système thermodynamique fermé, lorsqu'il passe d'un état initial à un état final de manière quasi-statique, c'est-à-dire suite à une succession d'états d'équilibre.
Travail sur des processus polytropiques pour différentes valeurs de n
Pour n ≠ 1
Le travail mécanique W effectué par un système thermodynamique fermé est calculé par l'expression:
W = ∫P.dV
Où P est la pression et V le volume.
Comme dans le cas d'un procédé polytropique, la relation entre la pression et le volume est:
P.V n = constant = C
Résolution de P à partir de l'expression précédente pour le remplacer dans l'expression de travail:
P = C /V n
Nous avons le travail mécanique effectué au cours d'un processus polytropique, qui commence dans un état initial 1 et se termine dans l'état final 2. Tout cela apparaît dans l'expression suivante:


C = P1 V1n = Pdeux Vdeuxn
En substituant la valeur de la constante dans l'expression de travail, on obtient:
W = (Pdeux Vdeux - P1 V1) / (1-n)
Dans le cas où la substance de travail peut être modélisée comme un gaz parfait, nous avons l'équation d'état suivante:
P.V = m.R.T
Où m est le nombre de moles du gaz parfait et R est la constante de gaz universelle.
Pour un gaz parfait qui suit un processus polytropique avec un indice de polytropie différent de l'unité et qui passe d'un état de température initiale T1 à un autre état avec la température Tdeux nous avons que le travail effectué est donné par la formule suivante:
W = m R (Tdeux - T1) / (1-n)
Pour n → ∞
Selon la formule du travail obtenu dans la section précédente, nous avons que le travail d'un processus polytropique avec n = ∞ est nul, car l'expression du travail est divisée par l'infini et donc le résultat tend vers zéro.
Une autre manière d'arriver à ce résultat est la relation P1 V1n = Pdeux Vdeuxn, qui peut être réécrit comme suit:
(P1/ Pdeux) = (Vdeux/ V1)n
En prenant la nième racine de chaque membre, nous obtenons:
(Vdeux/ V1) = (P1/ Pdeux)(1 / n)
Dans le cas où n → ∞, on a (Vdeux/ V1) = 1, ce qui signifie que:
Vdeux = V1
Autrement dit, le volume ne change pas dans un processus polytropique avec n → ∞. Par conséquent, le différentiel de volume dV dans l'intégrale du travail mécanique est de 0. Ces types de processus polytropiques sont également connus sous le nom de processus isochorique, ou processus à volume constant.
Pour n = 1
Encore une fois, nous avons l'expression l'expression du travail:
W = ∫P dV
Dans le cas d'un procédé polytropique avec n = 1, la relation entre la pression et le volume est:
P V = constante = C
En résolvant P à partir de l'expression précédente et en la remplaçant, nous avons le travail effectué pour passer de l'état initial 1 à l'état final 2:

C'est-à-dire:
W = C ln (Vdeux/ V1).
Comme les états initial et final sont bien déterminés, le ctte le sera aussi. C'est-à-dire:
C = P1 V1 = Pdeux Vdeux
Enfin, nous avons les expressions utiles suivantes pour trouver le travail mécanique d'un système fermé polytropique dans lequel n = 1.
W = P1 V1 ln (Vdeux/ V1) = Pdeux Vdeux ln (Vdeux/ V1)
Si la substance de travail consiste en m moles de gaz parfait, alors l'équation d'état du gaz parfait peut être appliquée: P V = m.R.T.
Dans ce cas, comme P.V1 = ctte, nous avons qu'un processus polytropique avec n = 1 est un processus à température constante T (isotherme), de sorte que les expressions suivantes pour le travail peuvent être obtenues:
W = m R T1 ln (Vdeux/ V1) = m R Tdeux ln (Vdeux/ V1)

Exemples de procédés polytropiques
- Exemple 1
Supposons un cylindre avec un piston mobile rempli d'un kilogramme d'air. Au départ, l'air occupe un volume V1= 0,2 m3 à une pression P1= 400 kPa. Un processus polytropique est suivi avec n = γ = 1,4, dont l'état final a la pression Pdeux = 100 kPa. Déterminer le travail effectué par l'air sur le piston.
Solution
Lorsque l'indice de polytropie est égal à la constante adiabatique, il y a un processus dans lequel la substance de travail (air) n'échange pas de chaleur avec l'environnement et, par conséquent, l'entropie ne change pas..
Pour l'air, gaz idéal diatomique, nous avons:
γ = Cp / Cv, avec Cp = (7/2) R et Cv = (5/2) R
Ensuite:
γ = 7/5 = 1,4
En utilisant l'expression du processus polytropique, le volume final de l'air peut être déterminé:
Vdeux = [(Pdeux V11,4) / Pdeux](1 / 1,4) = 0,54 m3.
Nous avons maintenant les conditions pour appliquer la formule du travail effectué dans un procédé polytropique pour n ≠ 1 obtenu ci-dessus:
W = (Pdeux Vdeux - P1 V1) / (1-n)
En remplaçant les valeurs appropriées que nous avons:
W = (100 kPa 0,54 m3 - 400 kPa 0,2 m3) / (1 - 1,4) = 65,4 kJ
- Exemple 2
Supposons le même cylindre de l'exemple 1, avec un piston mobile rempli d'un kilogramme d'air. Au départ, l'air occupe un volume V1 = 0,2 m3 à une pression P1 = 400 kPa. Mais contrairement au cas précédent, l'air se dilate de manière isotherme pour atteindre une pression finale P2 = 100 kPa. Déterminer le travail effectué par l'air sur le piston.
Solution
Comme vu précédemment, les processus isothermes sont des processus polytropiques d'indice n = 1, il est donc vrai que:
P1 V1 = P2 V2
De cette manière, le volume final peut être facilement décollé pour obtenir:
V2 = 0,8 m3
Ensuite, en utilisant l'expression de travail obtenue précédemment pour le cas n = 1, nous avons que le travail effectué par l'air sur le piston dans ce processus est:
W = P1 V1 ln (V2 / V1) = 400000 Pa × 0,2 m3 ln (0,8 / 0,2) = 110,9 kJ.
Les références
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
- Cengel, Y. 2012. Thermodynamique. 7e édition. Mcgraw Hill.
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 4. Fluides et thermodynamique. Edité par Douglas Figueroa (USB).
- López, C. La première loi de la thermodynamique. Récupéré de: culturacientifica.com.
- Knight, R. 2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique. Pearson.
- Serway, R., Vulle, C. 2011. Principes de base de la physique. 9e éd. Cengage Learning.
- Université de Séville. Machines thermiques. Récupéré de: laplace.us.es.
- Wikiwand. Procédé polytropique. Récupéré de: wikiwand.com.



Personne n'a encore commenté ce post.