
Propriétés croisées des produits, applications et exercices
le produit croisé ou produit vectoriel c'est une manière de multiplier deux ou plusieurs vecteurs. Il existe trois façons de multiplier les vecteurs, mais aucune de celles-ci n'est une multiplication au sens habituel du mot. L'une de ces formes est connue sous le nom de produit vectoriel, ce qui nous donne un troisième vecteur.
Le produit croisé, également appelé produit croisé ou produit externe, a différentes propriétés algébriques et géométriques. Ces propriétés sont très utiles, notamment dans l'étude de la physique..

Index des articles
- 1 Définition
- 2 propriétés
- 2.1 Propriété 1
- 2.2 Propriété 2
- 2.3 Propriété 3
- 2.4 Propriété 4 (produit triple dot)
- 2.5 Propriété 5 (produit vectoriel triple)
- 2.6 Propriété 6
- 2.7 Propriété 7
- 2.8 Propriété 8
- 3 applications
- 3.1 Calcul du volume d'un parallélépipède
- 4 exercices résolus
- 4.1 Exercice 1
- 4.2 Exercice 2
- 5 Références
Définition
Une définition formelle du produit vectoriel est la suivante: si A = (a1, a2, a3) et B = (b1, b2, b3) sont des vecteurs, alors le produit vectoriel de A et B, que nous désignerons par AxB, est:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
En raison de la notation AxB, il est lu comme "A cross B".
Un exemple d'utilisation du produit extérieur est que si A = (1, 2, 3) et B = (3, -2, 4) sont des vecteurs, alors en utilisant la définition d'un produit vectoriel, nous avons:
AxB = (1, 2, 3) x (3, -2, 4) = (2 * 4 - 3 * (- 2), 3 * 3 - 1 * 4, 1 * (- 2) - 2 * 3)
AxB = (8 + 6, 9 - 4, - 2 - 6) = (14, 5, - 8).
Une autre manière d'exprimer le produit vectoriel est donnée par la notation des déterminants.
Le calcul d'un déterminant du second ordre est donné par:
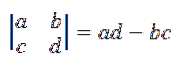
Par conséquent, la formule du produit croisé donnée dans la définition peut être réécrite comme suit:
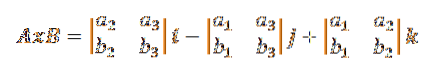
Ceci est généralement simplifié en un déterminant du troisième ordre comme suit:
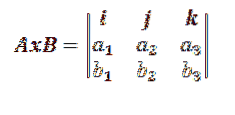
Où i, j, k représentent les vecteurs qui forment la base de R3.
En utilisant cette façon d'exprimer le produit croisé, nous avons que l'exemple précédent peut être réécrit comme:
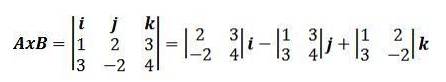
Propriétés
Certaines propriétés du produit vectoriel sont les suivantes:
Propriété 1
Si A est n'importe quel vecteur de R3, nous devons:
- AxA = 0
- Ax0 = 0
- 0xA = 0
Ces propriétés sont faciles à vérifier en utilisant uniquement la définition. Si A = (a1, a2, a3) nous avons:
AxA = (a2a3 - a3a2, a3a1 - a1a3, a1a2 - a2a1) = (0, 0, 0) = 0.
Ax0 = (a2 * 0 - a3 * 0, a3 * 0 - a1 * 0, a1 * 0 - a2 * 0) = (0, 0, 0) = 0.
Si i, j, k représentent la base unitaire de R3, nous pouvons les écrire comme suit:
i = (1, 0, 0)
j = (0, 1, 0)
k = (0, 0, 1)
Donc, nous avons que les propriétés suivantes sont vraies:
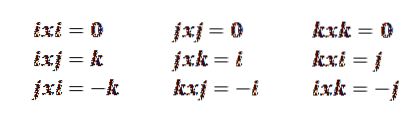
Comme règle mnémotechnique, le cercle suivant est souvent utilisé pour se souvenir de ces propriétés:
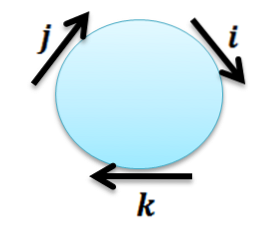
Là, il faut noter que tout vecteur avec lui-même donne le vecteur 0 comme résultat, et le reste des produits peut être obtenu avec la règle suivante:
Le produit croisé de deux vecteurs consécutifs dans le sens des aiguilles d'une montre donne le vecteur suivant; et quand on considère le sens anti-horaire, le résultat est le vecteur suivant avec signe négatif.
Grâce à ces propriétés, nous pouvons voir que le produit vectoriel n'est pas commutatif; par exemple, notez simplement que i x j ≠ j x i. La propriété suivante nous indique comment AxB et BxA sont liés en général.
Propriété 2
Si A et B sont des vecteurs de R3, nous devons:
AxB = - (BxA).
Manifestation
Si A = (a1, a2, a3) et B = (b1, b2, b3), par définition de produit externe on a:
AxB = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1)
= (- 1) (a3b2 - a2b3, a1b3 - a3b1, a2b1 - a1b2)
= (- 1) (BxA).
On voit aussi que ce produit n'est pas associatif avec l'exemple suivant:
ix (ixj) = ixk = - j mais (ixi) xj = 0xj = 0
De cela, nous pouvons voir que:
ix (ixj) ≠ (ixi) xj
Propriété 3
Si A, B, C sont des vecteurs de R3 et r est un nombre réel, ce qui suit est vrai:
- Axe (B + C) = AxB + AxC
- r (AxB) = (rA) xB = Ax (rB)
Grâce à ces propriétés nous pouvons calculer le produit vectoriel en utilisant les lois de l'algèbre, à condition que l'ordre soit respecté. Par exemple:
Si A = (1, 2, 3) et B = (3, -2, 4), nous pouvons les réécrire sur la base canonique de R3.
Ainsi, A = i + 2j + 3k et B = 3i - 2j + 4k. Ensuite, appliquez les propriétés précédentes:
AxB = (i + 2j + 3k) x (3i - 2j + 4k)
= 3 (ixi) - 2 (ixj) + 4 (ixk) + 6 (jxi) - 4 (jxj) + 8 (jxk) + 9 (kxi) - 6 (kxj) +12 (kxk)
= 3 (0) - 2 (k) + 4 (- j) + 6 (- k) - 4 (0) + 8 (i) + 9 (j) - 6 (- i) +12 (0)
= - 2k - 4j - 6k + 8i + 9j + 6i = 14i + 5j - 4k
= (14, 5, - 8).
Propriété 4 (produit triple dot)
Comme nous l'avons mentionné au début, il existe d'autres moyens de multiplier les vecteurs en plus du produit vectoriel. L'une de ces méthodes est le produit scalaire ou produit interne, qui est noté A ∙ B et dont la définition est:
Si A = (a1, a2, a3) et B = (b1, b2, b3), alors A ∙ B = a1b1 + a2b2 + a3b3
La propriété qui relie les deux produits est connue sous le nom de produit triple scalaire.
Si A, B et C sont des vecteurs de R3, alors A ∙ BxC = AxB ∙ C
A titre d'exemple, voyons que, étant donné A = (1, 1, - 2), B = (- 3, 4, 2) et C = (- 5, 1, - 4), cette propriété est remplie.
BxC = - 3k - 12j + 20k - 16i - 10j - 2i = - 18i - 22j + 17k
A ∙ BxC = (1, 1, - 2) ∙ (- 18, - 22, 17) = (1) (- 18) + (1) (- 22) + (- 2) (17) = - 74
D'autre part:
AxB = 4k - 2j + 3k + 2i + 6j + 8i = 10i + 4j + 7k
AxB ∙ C = (10, 4, 7) ∙ (- 5, 1, - 4) = (10) (- 5) + (4) (1) + (7) (- 4) = - 74
Un autre triple produit est Ax (BxC), connu sous le nom de produit triple vecteur..
Propriété 5 (produit triple vecteur)
Si A, B et C sont des vecteurs de R3, ensuite:
Axe (BxC) = (A ∙ C) B - (A ∙ B) C
A titre d'exemple, voyons que, étant donné A = (1, 1, - 2), B = (- 3, 4, 2) et C = (- 5, 1, - 4), cette propriété est remplie.
De l'exemple précédent, nous savons que BxC = (- 18, - 22, 17). Calculons Ax (BxC):
Hache (BxC) = - 22k - 17j + 18k + 17i + 36j - 44i = - 27i + 19j - 4k
D'autre part, nous devons:
A ∙ C = (1, 1, - 2) ∙ (- 5, 1, - 4) = (1) (- 5) + (1) (1) + (- 2) (- 4) = - 5 + 1 + 8 = 4
A ∙ B = (1, 1, - 2) ∙ (- 3, 4, 2) = (1) (- 3) + (1) (4) + (- 2) (2) = - 3 + 4 - 4 = - 3
Ainsi, nous devons:
(A ∙ C) B - (A ∙ B) C = 4 (- 3, 4, 2) + 3 (- 5, 1, - 4) = (- 12, 16, 8) + (- 15, 3, - 12) = (- 27,19, -4)
Propriété 6
C'est l'une des propriétés géométriques des vecteurs. Si A et B sont deux vecteurs dans R3 et ϴ est l'angle formé entre ceux-ci, alors:
|| AxB || = || A |||| B || sin (ϴ), où || ∙ || désigne le module ou la grandeur d'un vecteur.
L'interprétation géométrique de cette propriété est la suivante:
Soit A = PR et B = PQ. Ensuite, l'angle formé par les vecteurs A et B est l'angle P du triangle RQP, comme le montre la figure suivante.
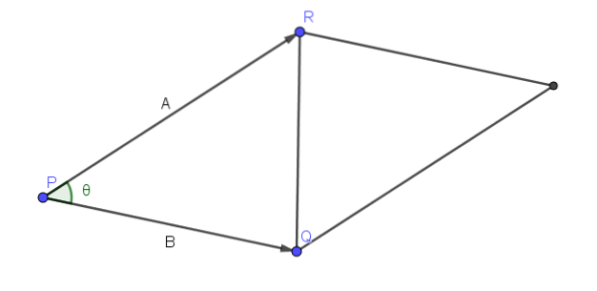
Par conséquent, l'aire du parallélogramme qui a PR et PQ comme côtés adjacents est || A |||| B || sin (ϴ), puisque l'on peut prendre comme base || A || et sa hauteur est donnée par || B || sin (ϴ).
Par cela, nous pouvons conclure que || AxB || est l'aire dudit parallélogramme.
Exemple
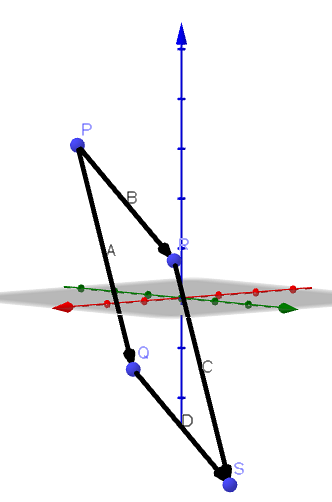
Étant donné les sommets suivants d'un quadrilatère P (1, -2,3), Q (4, 3, -1), R (2, 2,1) et S (5,7, -3), montrent que ledit quadrilatère est un parallélogramme et trouve sa surface.
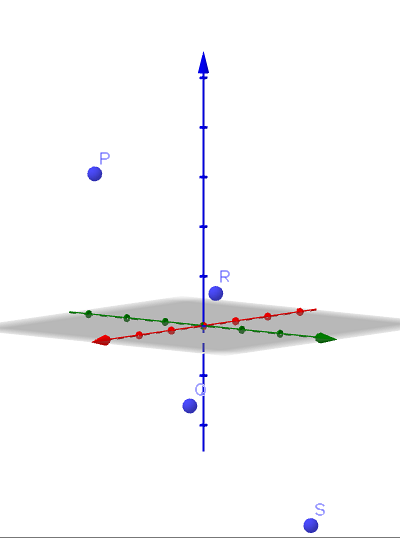
Pour cela, nous déterminons d'abord les vecteurs qui déterminent la direction des côtés du quadrilatère. C'est:
A = PQ = (1 - 4, 3 + 2, - 1 - 3) = (3, 5, - 4)
B = PR = (2 - 1, 2 + 2, 1 - 3) = (1, 4, - 2)
C = RS = (5 - 2, 7 - 2, - 3 - 1) = (3, 5, - 4)
D = QS = (5 - 4, 7 - 3, - 3 + 1) = (1, 4, - 2)
Comme nous pouvons le voir, A et C ont le même vecteur directeur, donc nous avons que les deux sont parallèles; la même chose se produit avec B et D.Par conséquent, nous concluons que PQRS est un parallélogramme.
Pour avoir l'aire de ce parallélogramme, nous calculons BxA:
BxA = (i + 4j - 2k) x (3i + 5j - 4k)
= 5k + 4j - 12k - 16i - 6j + 10i
= - 6i - 2j - 7k.
Par conséquent, la surface au carré sera:
|| BxA ||deux = (- 6)deux + (- deux)deux + (- 7)deux = 36 + 4 + 49 = 89.
On peut conclure que l'aire du parallélogramme sera la racine carrée de 89.
Propriété 7
Deux vecteurs A et B sont parallèles dans R3 si et seulement si AxB = 0
Manifestation
Il est clair que si A ou B sont le vecteur nul, il est satisfait que AxB = 0. Puisque le vecteur zéro est parallèle à tout autre vecteur, alors la propriété est valide.
Si aucun des deux vecteurs n'est le vecteur nul, nous avons que leurs magnitudes sont différentes de zéro; c'est-à-dire à la fois || A || ≠ 0 comme || B || ≠ 0, donc nous aurons || AxB || = 0 si et seulement si sin (ϴ) = 0, et cela se produit si et seulement si ϴ = π ou ϴ = 0.
Par conséquent, nous pouvons conclure AxB = 0 si et seulement si ϴ = π ou ϴ = 0, ce qui ne se produit que lorsque les deux vecteurs sont parallèles l'un à l'autre.
Propriété 8
Si A et B sont deux vecteurs dans R3, alors AxB est perpendiculaire à A et B.
Manifestation
Pour cette preuve, rappelons que deux vecteurs sont perpendiculaires si A ∙ B est égal à zéro. De plus, nous savons que:
A ∙ AxB = AxA ∙ B, mais AxA est égal à 0. On a donc:
A ∙ AxB = 0 ∙ B = 0.
Par cela, nous pouvons conclure que A et AxB sont perpendiculaires l'un à l'autre. De même, nous devons:
AxB ∙ B = A ∙ BxB.
Puisque BxB = 0, nous avons:
AxB ∙ B = A ∙ 0 = 0.
Par conséquent, AxB et B sont perpendiculaires l'un à l'autre et avec cela la propriété est démontrée. Ceci est très utile, car cela nous permet de déterminer l'équation d'un plan.
Exemple 1
Obtenir une équation du plan qui passe par les points P (1, 3, 2), Q (3, - 2, 2) et R (2, 1, 3).
Soit A = QR = (2 - 3.1 + 2, 3 - 2) et B = PR = (2 - 1.1 - 3, 3 - 2). Alors A = - i + 3j + k et B = i - 2j + k. Pour trouver le plan formé par ces trois points, il suffit de trouver un vecteur normal au plan, qui est AxB.
AxB = (- i + 3j + k) x (i - 2j + k) = 5i + 2j - k.
Avec ce vecteur, et en prenant le point P (1, 3, 2), on peut déterminer l'équation du plan comme suit:
(5, 2, - 1) ∙ (x - 1, y - 3, z - 2) = 5 (x - 1) + 2 (y - 3) - (z - 2) = 0
Ainsi, nous avons que l'équation du plan est 5x + 2y - z - 9 = 0.
Exemple 2
Trouvez l'équation du plan qui contient le point P (4, 0, - 2) et qui est perpendiculaire à chacun des plans x - y + z = 0 et 2x + y - 4z - 5 = 0 .
Sachant qu'un vecteur normal à un plan ax + by + cz + d = 0 est (a, b, c), on a que (1, -1,1) est un vecteur normal de x - y + z = 0 y (2,1, - 4) est un vecteur normal de 2x + y - 4z - 5 = 0.
Un vecteur normal au plan recherché doit donc être perpendiculaire à (1, -1,1) et à (2, 1, - 4). Ledit vecteur est:
(1, -1,1) x (2,1, - 4) = 3i + 6j + 3k.
Alors, on a que le plan recherché est celui qui contient le point P (4,0, - 2) et a le vecteur (3,6,3) comme vecteur normal.
3 (x - 4) + 6 (y - 0) + 3 (z + 2) = 0
x + 2y + z - 2 = 0.
Applications
Calcul du volume d'un parallélépipède
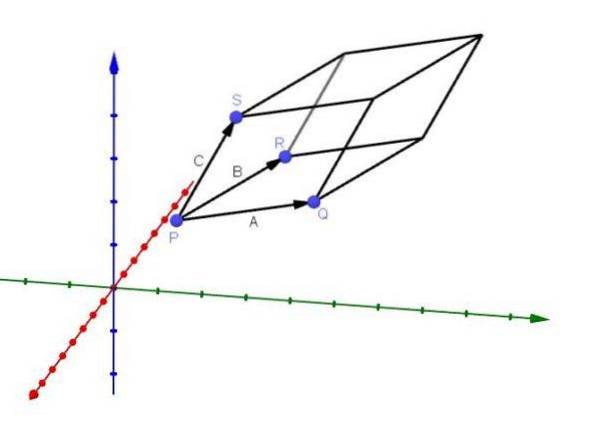
Une application qui a le triple produit scalaire est de pouvoir calculer le volume d'un parallélépipède dont les arêtes sont données par les vecteurs A, B et C, comme le montre la figure:
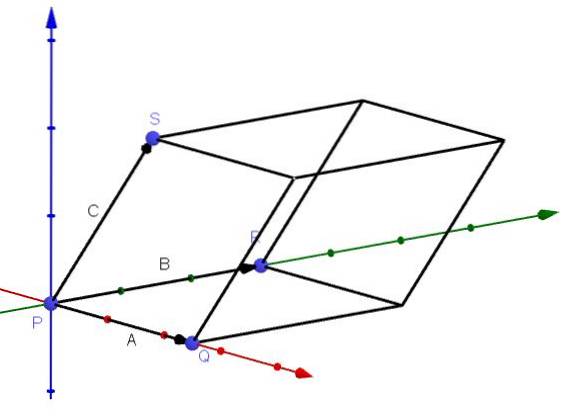
On peut déduire cette application de la manière suivante: comme on l'a dit précédemment, le vecteur AxB est un vecteur normal au plan de A et B. On a aussi que le vecteur - (AxB) est un autre vecteur normal audit plan.
On choisit le vecteur normal qui forme le plus petit angle avec le vecteur C; sans perte de généralité, soit AxB le vecteur dont l'angle avec C est le plus petit.
Nous avons que AxB et C ont le même point de départ. De plus, on sait que l'aire du parallélogramme qui forme la base du parallélépipède est || AxB ||. Donc, si la hauteur du parallélépipède est donnée par h, on a que son volume sera:
V = || AxB || h.
D'un autre côté, considérons le produit scalaire entre AxB et C, qui peut être décrit comme suit:
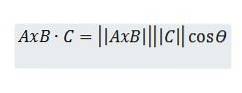
Cependant, par propriétés trigonométriques, nous avons que h = || C || cos (ϴ), donc nous avons:
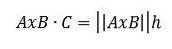
De cette façon, nous avons cela:
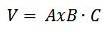
De manière générale, nous avons que le volume d'un parallélépipède est donné par la valeur absolue du produit triple scalaire AxB ∙ C.
Exercices résolus
Exercice 1
Étant donné les points P = (5, 4, 5), Q = (4, 10, 6), R = (1, 8, 7) et S = (2, 6, 9), ces points forment un parallélépipède dont les arêtes ce sont PQ, PR et PS. Déterminer le volume dudit parallélépipède.
Solution
Si nous prenons:
- A = PQ = (-1, 6, 1)
- B = PR = (-4, 4, 2)
- C = PS = (-3, 2, 2)
En utilisant la propriété du produit triple scalaire, nous avons:
AxB = (-1, 6, 1) x (-4, 4, 2) = (8, -2, 20).
AxB ∙ C = (8, -2, 20) ∙ (-3, 2, 2) = -24 -4 +80 = 52.
Par conséquent, nous avons que le volume dudit parallélépipède est de 52.
Exercice 2
Déterminer le volume d'un parallélépipède dont les arêtes sont données par A = PQ, B = PR et C = PS, où les points P, Q, R et S sont (1, 3, 4), (3, 5, 3), (2, 1, 6) et (2, 2, 5), respectivement.
Solution
Nous avons d'abord que A = (2, 2, -1), B = (1, -2, 2), C = (1, -1, 1).
Nous calculons AxB = (2, 2, -1) x (1, -2, 2) = (2, -5, -6).
Ensuite, nous calculons AxB ∙ C:
AxB ∙ C = (2, -5, -6) ∙ (1, -1, 1) = 2 + 5 - 6 = 1.
On en conclut donc que le volume dudit parallélépipède est de 1 unité cubique.
Les références
- Leithold, L. (1992). Le calcul avec la géométrie analytique. HARLA, S.A.
- Resnick, R., Halliday, D. et Krane, K. (2001). Physique Vol.1. Mexique: Continental.
- Saenz, J. (s.f.). Calcul vectoriel 1ed. Hypoténuse.
- Spiegel, M. R. (2011). Analyse vectorielle 2ed. Mc Graw Hill.
- Zill, D. G. et Wright, W. (2011). Calcul de plusieurs variables 4ed. Mc Graw Hill.



Personne n'a encore commenté ce post.