
Addition de propriété associative, multiplication, exemples, exercices
La propriété associative de la somme représente le caractère associatif de l'opération de somme dans divers ensembles mathématiques. Dans celui-ci, trois éléments (ou plus) de ces ensembles sont liés, appelés a, b et c, de sorte que c'est toujours vrai:
a + (b + c) = (a + b) + c
De cette manière, il est garanti que, quelle que soit la manière de regrouper pour effectuer l'opération, le résultat est le même.

Mais il faut noter que la propriété associative n'est pas synonyme de propriété commutative. Autrement dit, nous savons que l'ordre des ajouts ne modifie pas la somme ou que l'ordre des facteurs ne modifie pas le produit. Donc, pour la somme, cela peut s'écrire comme ceci: a + b = b + a.
Cependant, dans la propriété associative, c'est différent, car l'ordre des éléments à ajouter est conservé et ce qui change est l'opération qui est exécutée en premier. Ce qui signifie qu'il n'a pas d'importance d'ajouter d'abord (b + c) et à ce résultat ajouter a, que de commencer à ajouter a avec b et au résultat ajouter c.
De nombreuses opérations importantes telles que l'addition sont associatives, mais pas toutes. Par exemple, dans la soustraction de nombres réels, il arrive que:
a - (b - c) ≠ (a - b) - c
Si a = 2, b = 3, c = 1, alors:
2- (3 - 1) ≠ (2 - 3) - 1
0 ≠ -2
Index des articles
- 1 Propriété associative de multiplication
- 1.1 Applications de la propriété associative de multiplication
- 2 exemples
- 2.1 La propriété associative dans les vecteurs
- 2.2 Factorisation des polynômes par regroupement de termes
- 3 exercices
- 3.1 - Exercice 1
- 3.2 - Exercice 2
- 4 Références
Propriété associative de multiplication
Comme cela a été fait pour l'addition, la propriété associative de multiplication stipule que:
a ˟ (b ˟ c) = (a ˟ b) ˟ c
Dans le cas de l'ensemble des nombres réels, il est facile de vérifier que c'est toujours le cas. Par exemple, en utilisant les valeurs a = 2, b = 3, c = 1, nous avons:
deux ˟ (3 ˟ 1) = (2 ˟ 3) ˟ 1 → 2 ˟ 3 = 6 ˟ 1
6 = 6
Les nombres réels remplissent la propriété associative d'addition et de multiplication. Par contre, dans un autre ensemble, tel que celui des vecteurs, la somme est associative, mais le produit croisé ou produit vectoriel ne l'est pas..
Applications de la propriété associative de multiplication
Un avantage des opérations dans lesquelles la propriété associative est remplie est de pouvoir regrouper de la manière la plus commode. Cela rend la résolution beaucoup plus facile..
Par exemple, supposons que dans une petite bibliothèque il y ait 3 étagères avec 5 étagères chacune. Dans chaque étagère, il y a 8 livres. Combien de livres y a-t-il au total?
On peut effectuer l'opération comme ceci: total des livres = (3 x 5) x 8 = 15 x 8 = 120 livres.
Ou comme ceci: 3 x (5 x 8) = 3 x 40 = 120 livres.

Exemples
-Dans les ensembles de nombres naturels, entiers, rationnels, réels et complexes, la propriété associative d'addition et de multiplication est remplie.
-Pour les polynômes s'appliquent également à ces opérations.
-Dans les cas d'opérations de soustraction, de division et d'exponentiation, la propriété associative n'est remplie ni en nombres réels ni en polynômes.
-Dans le cas des matrices, la propriété associative est valable pour l'addition et la multiplication, bien que dans ce dernier cas, la commutativité ne soit pas satisfaite. Cela signifie que, compte tenu des matrices A, B et C, il est vrai que:
(A x B) x C = A x (B x C)
Mais ... A x B ≠ B x A
La propriété associative dans les vecteurs
Les vecteurs forment un ensemble différent des nombres réels ou des nombres complexes. Les opérations définies pour l'ensemble des vecteurs sont quelque peu différentes: il y a l'addition, la soustraction et trois types de produits.
La somme des vecteurs remplit la propriété associative, tout comme les nombres, les polynômes et les matrices. Quant aux produits scalaires, scalaires par vecteurs et croisés entre vecteurs, ces derniers ne le remplissent pas, mais le produit scalaire, qui est un autre type d'opération entre vecteurs, le remplit en tenant compte de ce qui suit:
-Le produit d'un scalaire et d'un vecteur donne un vecteur.
-Et lors de la multiplication scalaire de deux vecteurs, il en résulte un scalaire.
Par conséquent, étant donné les vecteurs v, ou alors Oui w, et en plus un scalaire λ, il est possible d'écrire:
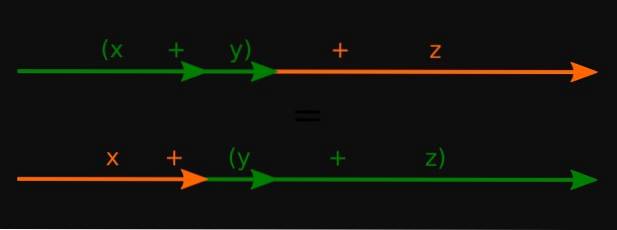
-Somme des vecteurs: v +(ou alors + w ) = (v + ou alors) + w
-Produit scalaire: λ (v • ou alors ) = (λv) • ou alors
Ce dernier est possible grâce à v • ou alors donne un scalaire, et λv c'est un vecteur.
Cependant:
v × (ou alors × w ) ≠ (v × ou alors)×w
Factorisation des polynômes par regroupement de termes
Cette application est très intéressante, car comme on l'a dit précédemment, la propriété associative permet de résoudre certains problèmes. La somme des monômes est associative et peut être utilisée pour factoriser lorsqu'un facteur commun évident n'apparaît pas à première vue.
Par exemple, supposons que vous demandiez de factoriser: X3 + deuxXdeux + 3X +6. Ce polynôme n'a pas de facteur commun, mais voyons ce qui se passe s'il est groupé comme ceci:
X3 + 2xdeux + 3x +6 = (x3 + 2xdeux) + (3x +6)
La première parenthèse a pour point commun Xdeux:
X3 + deuxXdeux = Xdeux (x + 2)
Dans le second, le facteur commun est 3:
3x +6 = 3 (x + 2)
Ensuite:
X3 + deuxXdeux + 3X +6 = Xdeux(x + 2) + 3 (x + 2)
Maintenant, il y a un facteur commun évident, qui est x + 2:
Xdeux(x + 2) + 3 (x + 2) = (x + 2) (xdeux+3)
Exercices
- Exercice 1
Un bâtiment scolaire a 4 étages et chacun a 12 salles de classe avec 30 bureaux à l'intérieur. Combien de bureaux l'école a-t-elle au total?
Solution
Ce problème est résolu en appliquant la propriété associative de multiplication, voyons:
Nombre total de bureaux = 4 étages x 12 salles de classe / étage x 30 bureaux / salle de classe = (4 x 12) x 30 bureaux = 48 x 30 = 1440 bureaux.
Ou si vous préférez: 4 x (12 x 30) = 4 x 360 = 1440 bureaux
- Exercice 2
Compte tenu des polynômes:
A (x) = 5x3 + 2xdeux -7x + 1
B (x) = x4 +6x3 -5x
C (x) = -8xdeux +3x -7
Appliquez la propriété associative d'addition pour trouver A (x) + B (x) + C (x).
Solution
Vous pouvez regrouper les deux premiers et ajouter le troisième au résultat:
A (x) + B (x) = [5x3 + 2xdeux -7x + 1] + [x4 +6x3 -5x] = x4 + 11x3+ 2xdeux -12x +1
Immédiatement, le polynôme C (x) est ajouté:
[X4 + 11x3+ 2xdeux -12x +1] + [-8xdeux +3x -7] = x4 + 11x3 - 6xdeux -9x -6
Le lecteur peut vérifier que le résultat est identique s'il est résolu au moyen de l'option A (x) + [B (x) + C (x)].
Les références
- Jiménez, R. 2008. Algèbre. Prentice Hall.
- Les mathématiques sont amusantes: lois commutatives, associatives et distributives. Récupéré de: mathisfun.com.
- Entrepôt de mathématiques. Définition de la propriété associative. Récupéré de: mathwarehouse.com.
- Découvrir. Propriété associative et commutative d'addition et de multiplication (avec exemples). Récupéré de: scaimer.com.
- Wikipédia. Propriété associative. Récupéré de: en.wikipedia.org.


Personne n'a encore commenté ce post.