
Quel est l'équilibre de la particule? (Avec des exemples)
le équilibre des particules C'est un état dans lequel une particule se trouve lorsque les forces externes qui agissent sur elles s'annulent mutuellement. Cela suppose qu'il maintient un état constant, de telle sorte qu'il peut se produire de deux manières différentes en fonction de la situation spécifique.
Le premier est d'être en équilibre statique, dans lequel la particule est immobile; et le second est l'équilibre dynamique, où la somme des forces s'annule, mais néanmoins la particule a un mouvement rectiligne uniforme.

Le modèle de particules est une approximation très utile pour étudier le mouvement d'un corps. Elle consiste à supposer que toute la masse du corps est concentrée en un seul point, quelle que soit la taille de l'objet. De cette façon, vous pouvez représenter une planète, une voiture, un électron ou une boule de billard.
Index des articles
- 1 La force résultante
- 2 schémas de corps libres
- 3 façons d'appliquer la condition d'équilibre
- 3.1 Deux forces de même ampleur et de direction et de directions opposées
- 3.2 Deux forces de grandeur différente, même direction et directions opposées
- 3.3 Deux forces de même ampleur et de direction différente
- 3.4 Trois forces avec une direction différente
- 4 frottements
- 4.1 Le frottement dynamique
- 5 Exemple travaillé
- 5.1 Solution
- 6 Références
La force résultante
Le point qui représente l'objet est l'endroit où les forces qui l'affectent agissent. Toutes ces forces peuvent être remplacées par une seule qui fait le même effet, qui s'appelle force résultante ou alors force nette et est noté FR ou FN.
Selon la deuxième loi de Newton, lorsqu'il y a une force résultante déséquilibrée, le corps subit une accélération proportionnelle à la force:
FR = m.a
Où à est l'accélération que l'objet acquiert grâce à l'action de la force et m est la masse de l'objet. Que se passe-t-il si le corps n'est pas accéléré? Précisément ce qui a été indiqué au début: le corps est au repos ou se déplace avec un mouvement rectiligne uniforme, qui manque d'accélération.
Pour une particule en équilibre, il est valable de s'assurer que:
FR = 0
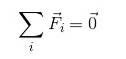
Puisque l'ajout de vecteurs n'implique pas nécessairement l'ajout des modules, les vecteurs doivent être décomposés. Ainsi, il est valable d'exprimer:
FX = m.aX = 0; FOui = m.aOui = 0; Fz = m.az = 0
Diagrammes de corps libre
Afin de visualiser les forces qui agissent sur la particule, il est pratique de faire un diagramme de corps libre, dans lequel toutes les forces qui agissent sur l'objet sont représentées par des flèches..
Les équations ci-dessus sont de nature vectorielle. Lors de la décomposition des forces, elles se distinguent par des signes. De cette façon, il est possible que la somme de ses composants soit nulle.
Voici des conseils importants pour rendre le dessin utile:
- Choisissez un système de référence dans lequel la plus grande quantité de forces se situe sur les axes de coordonnées.
- Le poids est toujours dessiné verticalement vers le bas.
- Dans le cas de deux ou plusieurs surfaces en contact, il existe des forces normales, qui sont toujours tirées en poussant le corps et perpendiculairement à la surface qui l'exerce..
- Pour une particule en équilibre il peut y avoir des frottements parallèles à la surface de contact et s'opposant au mouvement possible, si la particule est considérée au repos, ou définitivement en opposition, si la particule se déplace avec MRU (mouvement rectiligne uniforme).
- S'il y a une corde, la tension est toujours tirée le long de celle-ci et tirant le corps.
Façons d'appliquer la condition d'équilibre
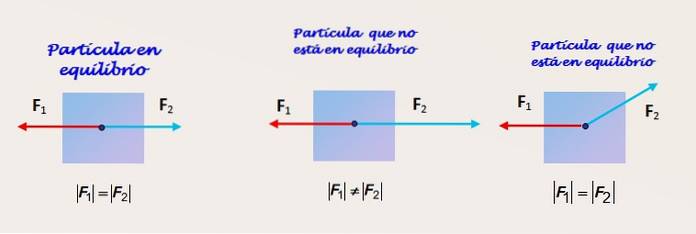
Deux forces d'amplitude égale et de direction et de directions opposées
La figure 2 montre une particule sur laquelle agissent deux forces. Dans la figure de gauche, la particule reçoit l'action de deux forces F1 et Fdeux qui ont la même grandeur et agissent dans la même direction et dans des directions opposées.
La particule est en équilibre, mais néanmoins avec les informations fournies il n'est pas possible de savoir si l'équilibre est statique ou dynamique. Plus d'informations sont nécessaires sur le référentiel inertiel à partir duquel l'objet est observé.
Deux forces de magnitude différente, de même direction et de directions opposées
La figure au centre montre la même particule, qui cette fois n'est pas en équilibre, puisque l'amplitude de la force Fdeux est supérieur à celui de F1. Il y a donc une force déséquilibrée et l'objet a une accélération dans le même sens que Fdeux.
Deux forces de même ampleur et de direction différente
Enfin, sur la figure de droite, nous voyons un corps qui n'est pas non plus en équilibre. Malgré le fait que F1 et Fdeux ont une magnitude égale, la force Fdeux n'est pas dans la même direction que 1. La composante verticale de Fdeux n'est contrecarré par aucun autre et la particule subit une accélération dans cette direction.
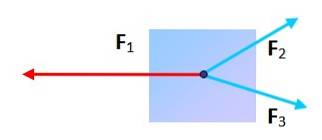
Trois forces avec une direction différente
Une particule soumise à trois forces peut-elle être en équilibre? Oui, tant que lorsque vous placez la fin et la fin de chacun d'eux, la figure résultante est un triangle. Dans ce cas, la somme vectorielle est nulle.
Friction
Une force qui intervient fréquemment dans l'équilibre de la particule est le frottement statique. Cela est dû à l'interaction de l'objet représenté par la particule avec la surface d'un autre. Par exemple, un livre en équilibre statique sur une table inclinée est modélisé comme une particule et possède un diagramme à corps libre comme celui-ci:
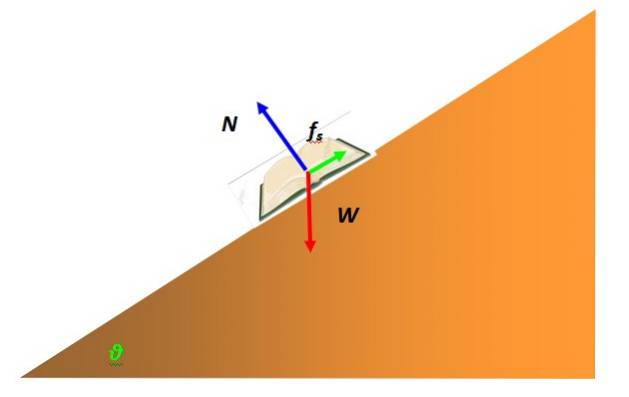
La force qui empêche le livre de glisser sur la surface du plan incliné et de rester au repos est le frottement statique. Cela dépend de la nature des surfaces en contact, qui présentent au microscope une rugosité avec des pics qui s'imbriquent les uns avec les autres, ce qui rend le mouvement difficile..
La valeur maximale du frottement statique est proportionnelle à la force normale, la force exercée par la surface sur l'objet supporté, mais perpendiculaire à ladite surface. Dans l'exemple du livre, il est indiqué en bleu. Mathématiquement, il est exprimé comme ceci:
Fs plus∝ N
La constante de proportionnalité est la coefficient de frottement statique μs, qui est déterminée expérimentalement, est sans dimension et dépend de la nature des surfaces en contact.
Fs max = μs N
Le frottement dynamique
Si une particule est en équilibre dynamique, le mouvement a déjà lieu et le frottement statique n'intervient plus. Si une force de frottement est présente qui s'oppose au mouvement, le frottement dynamique agit, dont la grandeur est constante et est donnée par:
Fk = μk N
Où μk c'est lui coefficient de frottement dynamique, Cela dépend également du type de surfaces en contact. Comme le coefficient de frottement statique, il est sans dimension et sa valeur est déterminée expérimentalement.
La valeur du coefficient de frottement dynamique est généralement inférieure à celle du frottement statique.
Exemple travaillé
Le livre de la figure 3 est au repos et a une masse de 1,30 kg. L'avion a un angle d'inclinaison de 30 °. Trouvez le coefficient de frottement statique entre le livre et la surface plane.
Solution
Il est important de sélectionner un système de référence adapté, voir la figure suivante:
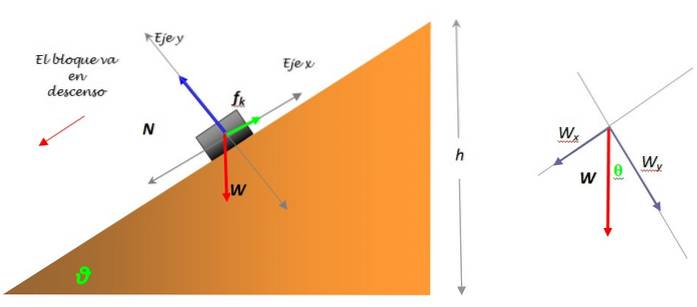
Le poids du livre a une ampleur W = mg, cependant il est nécessaire de le décomposer en deux composants: WX Oui WOui, car c'est la seule force qui ne tombe pas juste au-dessus de l'un des axes de coordonnées. La décomposition du poids est observée sur la figure de gauche.
WOui = mg.cosθ = 1,30 x 9,8 x cos 30º N = 11,03 N
WX = mg sinθ = 1,30 x 9,8 x sin 30º = 6,37 N
Le 2ème. La loi de Newton pour l'axe vertical est:
N - Wy = 0
N = mg. cos θ = 11,03 N.
Appliquer le 2ème. Loi de Newton pour l'axe des x, en choisissant la direction du mouvement possible comme positive:
WX - Fs = 0
Le frottement maximum est Fs max= μsN, donc:
WX - μsN = 0
μs = WX / N = 6,37 / 11,03 = 0,58
Les références
- Rex, A. 2011. Fondamentaux de la physique. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7ma. Ed. Cengage Learning. 120 - 124.
- Serway, R., Vulle, C. 2011. Principes de base de la physique. 9n / A Ed. Cengage Learning. 99-112.
- Tippens, P. 2011. Physique: concepts et applications. 7e édition. MacGraw Hill. 71 - 87.
- Walker, J. 2010. Physique. Addison Wesley. 148-164.



Personne n'a encore commenté ce post.