
Qu'est-ce qu'un géoïde?
le géoïde La figure de la Terre est la surface théorique de notre planète, déterminée par le niveau moyen des océans et de forme assez irrégulière. Mathématiquement, elle est définie comme la surface équipotentielle du potentiel gravitationnel effectif de la Terre, au niveau de la mer.
Comme il s'agit d'une surface imaginaire (non matérielle), elle traverse les continents et les montagnes, comme si tous les océans étaient reliés par des canaux d'eau qui traversent les terres émergées..

La Terre n'est pas une sphère parfaite, puisque la rotation autour de son axe la transforme en une sorte de boule aplatie par les pôles, avec des vallées et des montagnes. C'est pourquoi la forme sphéroïde est toujours inexacte.
Cette même rotation ajoute une force centrifuge à la force de gravité terrestre, dont la force résultante ou effective ne pointe pas vers le centre de la Terre, mais a un certain potentiel gravitationnel qui lui est associé..
Ajouté à cela, les accidents géographiques créent des irrégularités de densité, et donc la force d'attraction gravitationnelle dans certaines zones cesse définitivement d'être centrale..
Ainsi, les scientifiques, à commencer par C. F. Gauss, qui a conçu le géoïde original en 1828, ont créé un modèle géométrique et mathématique pour représenter plus précisément la surface de la Terre..
Pour cela, un océan est supposé au repos, sans marées ni courants océaniques et à densité constante, dont la hauteur sert de référence. On considère alors que la surface de la Terre ondule doucement, s'élevant là où la gravité locale est la plus élevée et s'enfonçant lorsqu'elle diminue..
Dans ces conditions, que l'accélération gravitationnelle effective soit toujours perpendiculaire à la surface dont les points sont au même potentiel et le résultat est le géoïde, qui est irrégulier puisque l'équipotentiel n'est pas symétrique.
Index des articles
- 1 Fondation physique du géoïde
- 1.1 Le potentiel gravitationnel de la Terre
- 2 Différences entre le géoïde et l'ellipsoïde
- 2.1 Les ondulations du géoïde
- 3 Avantages de représenter la Terre comme un géoïde
- 4 Références
Fondation physique du géoïde
Pour déterminer la forme du géoïde, qui s'est affinée au fil du temps, les scientifiques ont effectué de nombreuses mesures, en tenant compte de deux facteurs:
- Le premier est que la valeur de g, le champ gravitationnel de la Terre équivalent à l'accélération de la gravité, dépend de la latitude: maximum aux pôles et minimum à l'équateur.
- La seconde est que, comme nous l'avons déjà dit, la densité de la Terre n'est pas homogène. Il y a des endroits où ça augmente car les roches sont plus denses, il y a une accumulation de magma ou il y a beaucoup de sol en surface, comme une montagne par exemple.
Où la densité est plus élevée, g donc est-il. Noter que g est un vecteur et c'est pourquoi il est noté en gras.
Le potentiel gravitationnel de la Terre
Pour définir le géoïde, le potentiel dû à la gravité est nécessaire, pour lequel le champ gravitationnel doit être défini comme la force gravitationnelle par unité de masse.
Si une masse d'essai m est placé dans ledit champ, la force exercée par la Terre sur elle est son poids P = mg, donc la magnitude du champ est:
Force / masse = P / m = g
On connaît déjà sa valeur moyenne: 9,8 m / sdeux et si la Terre était sphérique, elle serait dirigée vers son centre. De même, selon la loi de Newton de la gravitation universelle:
P = Gm M / rdeux
Où M est la masse de la Terre et G est la constante universelle de gravitation. Puis la magnitude du champ gravitationnel g c'est:
g = GM / rdeux
Cela ressemble beaucoup à un champ électrostatique, donc un potentiel gravitationnel peut être défini qui est analogue à électrostatique:
V = -GM / r
La constante G est la constante universelle de la gravitation. Eh bien, les surfaces sur lesquelles le potentiel gravitationnel a toujours la même valeur sont appelées surfaces équipotentielles Oui g il leur est toujours perpendiculaire, comme dit précédemment.
Pour cette classe particulière de potentiel, les surfaces équipotentielles sont des sphères concentriques. Le travail nécessaire pour déplacer une masse sur eux est nul, car la force est toujours perpendiculaire à n'importe quel chemin sur l'équipotentiel.
Composante latérale de l'accélération de la gravité
Puisque la Terre n'est pas sphérique, l'accélération de la gravité doit avoir une composante latérale gl due à l'accélération centrifuge, causée par le mouvement de rotation de la planète autour de son axe.
La figure suivante montre ce composant en vert, dont la magnitude est:
gl = ωdeuxà
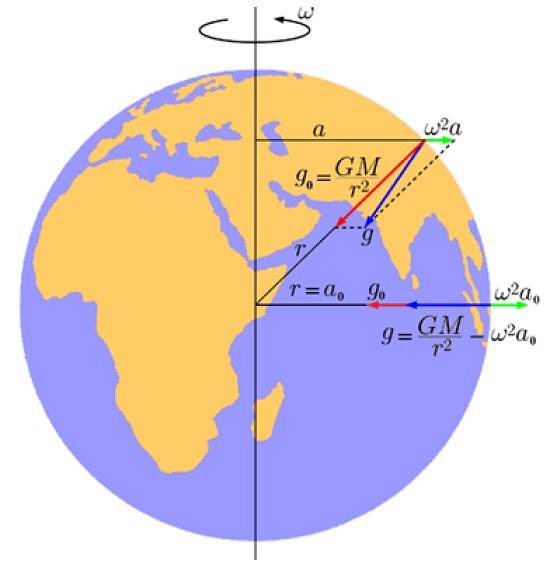
Dans cette équation ω est la vitesse angulaire de rotation de la Terre et à est la distance entre le point sur la Terre, à une certaine latitude, et l'axe.
Et en rouge se trouve le composant dû à l'attraction gravitationnelle planétaire:
gou alors = GM / rdeux
En conséquence, en ajoutant des vecteurs gou alors + gl, une accélération résultante se produit g (en bleu) qui est la véritable accélération de la gravité de la Terre (ou accélération effective) et qui, comme on le voit, ne pointe pas exactement vers le centre.
De plus, la composante latérale dépend de la latitude: elle est nulle aux pôles et donc le champ gravitationnel y est maximal. A l'équateur il s'oppose à l'attraction gravitationnelle, réduisant la gravité effective, dont la magnitude reste:
g = GM / rdeux - ωdeuxR
Avec R = rayon équatorial de la Terre.
On comprend maintenant que les surfaces équipotentielles de la Terre ne sont pas sphériques, mais prennent une forme telle que g être toujours perpendiculaire à eux en tous points.
Différences entre géoïde et ellipsoïde
Voici le deuxième facteur qui influe sur la variation du champ gravitationnel terrestre: les variations locales de gravité. Il y a des endroits où la gravité augmente parce qu'il y a plus de masse, par exemple sur la colline de la figure a).
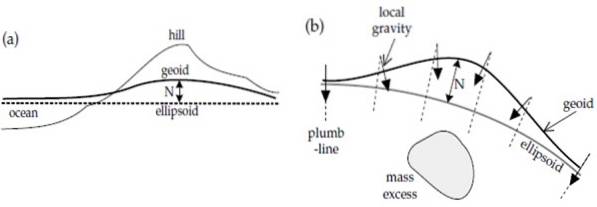
Ou il y a une accumulation ou un excès de masse sous la surface, comme en b). Dans les deux cas, il y a une élévation du géoïde car plus la masse est grande, plus l'intensité du champ gravitationnel est grande..
Par contre, au-dessus de l'océan, la densité est plus faible et par conséquent le géoïde coule, comme on le voit à gauche de la figure a), au-dessus de l'océan..
De la figure b), on peut également voir que la gravité locale, indiquée par des flèches, est toujours perpendiculaire à la surface du géoïde, comme nous l'avons dit. Cela ne se produit pas toujours avec l'ellipsoïde de référence.
Les ondulations du géoïde
La figure indique également, avec une flèche bidirectionnelle, la différence de hauteur entre le géoïde et l'ellipsoïde, qui est appelée ondulation y est noté N.Les ondulations positives sont liées à l'excès de masse et les ondulations négatives aux défauts.
Les ondulations ne dépassent presque jamais 200 m. En fait, les valeurs dépendent de la manière dont le niveau de la mer qui sert de référence est choisi, car certains pays choisissent différemment en fonction de leurs caractéristiques régionales.
Avantages de représenter la Terre comme un géoïde
-Sur le géoïde le potentiel effectif, résultat du potentiel dû à la gravité et au potentiel centrifuge, est constant.
-La force de gravité agit toujours perpendiculairement au géoïde et l'horizon lui est toujours tangentiel.
-Le géoïde offre une référence pour les applications de cartographie de haute précision.
-En utilisant le géoïde, les sismologues peuvent détecter la profondeur à laquelle les tremblements de terre se produisent.
-Le positionnement du GPS dépend du géoïde à utiliser comme référence.
-La surface de l'océan est également parallèle au géoïde.
-Les élévations et les descentes du géoïde indiquent les excès ou les défauts de masse, qui sont les anomalies gravimétriques. Lorsqu'une anomalie est détectée et en fonction de sa valeur, il est possible d'en déduire la structure géologique du sous-sol, au moins à certaines profondeurs..
C'est le fondement des méthodes gravimétriques en géophysique. Une anomalie gravimétrique peut indiquer des accumulations de certains minéraux, des structures enfouies sous terre, voire des espaces vides. Les dômes de sel dans le sous-sol, détectables par des méthodes gravimétriques, indiquent dans certains cas la présence d'hydrocarbures.
Les références
- CETTE. Euronews. L'emprise de la gravité sur la Terre. Récupéré de: youtube.com.
- JOIE. Géoïde. Récupéré de: youtube.com.
- Griem-Klee, S. Explorations minières: gravimétrie. Récupéré de: geovirtual2.cl.
- Lowrie, W. 2007. Fondamentaux de la géophysique. 2ème. Édition. la presse de l'Universite de Cambridge.
- NOAA. Quel est le géoïde?. Récupéré de: geodesy.noaa.gov.
- Sheriff, R. 1990. Géophysique appliquée. 2ème. Édition. la presse de l'Universite de Cambridge.



Personne n'a encore commenté ce post.