
Lignes caractéristiques obliques, équations et exemples
le lignes obliques Ce sont ceux qui sont inclinés, soit par rapport à une surface plane, soit par rapport à une autre droite qui indique une direction particulière. À titre d'exemple, considérons les trois lignes tracées dans un plan qui apparaissent dans la figure suivante.
Nous connaissons leurs positions relatives respectives car nous les comparons à une ligne de référence, qui est généralement la Axe X désignant l'horizontale.
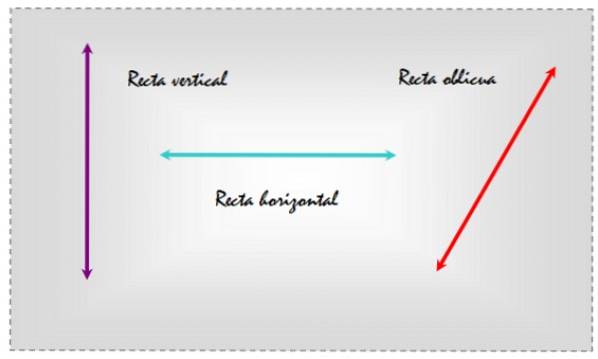
De cette manière, en choisissant l'horizontale comme référence, la ligne de gauche est verticale, celle du centre est horizontale et celle de droite est oblique, puisqu'elle est inclinée par rapport aux lignes de référence quotidiennes..
Or, les lignes qui sont sur le même plan, comme la surface du papier ou l'écran, occupent des positions relatives entre eux, selon qu'ils se croisent ou non. Dans le premier cas, ce sont des lignes sécantes, tandis que dans le second, elles sont parallèles.
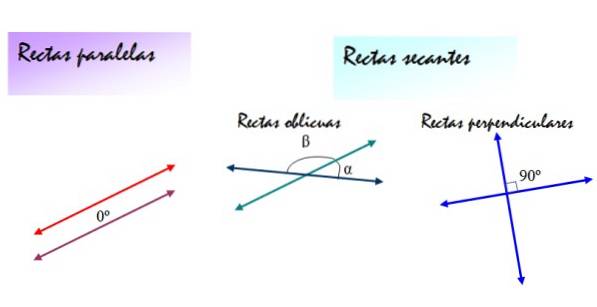
Par contre, les lignes sécantes peuvent être des lignes obliques ou des lignes perpendiculaires. Dans les deux cas, les pentes des droites sont différentes, mais les droites obliques forment entre elles des angles α et β différents de 90 °, tandis que les angles déterminés par les droites perpendiculaires sont toujours de 90 °..
La figure suivante résume ces définitions:
Index des articles
- 1 équations
- 1.1 Équation de la ligne dans le plan
- 2 Exemples de lignes obliques
- 2.1 Rayons de lumière
- 2.2 Lignes qui ne sont pas dans le même plan
- 3 Références
Équations
Pour connaître les positions relatives des lignes dans le plan, il est nécessaire de connaître l'angle qu'elles forment entre elles. Notez que les lignes sont:
Parallèle: s'ils ont la même pente (même direction) et ne se croisent jamais, donc leurs points sont équidistants.
Coïncident: lorsque tous ses points coïncident et ont donc la même pente, mais que la distance entre ses points est nulle.
Séchage: si leurs pentes sont différentes, la distance entre leurs points varie et l'intersection est un seul point.
Donc, une façon de savoir si deux lignes dans le plan sont sécantes ou parallèles est par leur pente. Les critères de parallélisme et de perpendicularité des droites sont les suivants:
Soit L deux lignes1 et moideux appartenant à un plan, dont les pentes sont respectivement m1 et Mdeux. Ces lignes sont parallèles si m1 = mdeux et sont perpendiculaires lorsque m1= -1 / mdeux
Si, connaissant les pentes de deux droites dans le plan, aucun des critères précédents n'est satisfait, on en conclut que les droites sont obliques. Connaissant deux points d'une ligne, la pente est calculée immédiatement, comme nous le verrons dans la section suivante.
Il est possible de savoir si deux droites sont sécantes ou parallèles en trouvant leur intersection, en résolvant le système d'équations qu'elles forment: s'il y a une solution elles sont sécantes, s'il n'y a pas de solution elles sont parallèles, mais si les solutions sont infini, les lignes coïncident.
Cependant, ce critère ne nous renseigne pas sur l'angle entre ces lignes, même si elles se croisent.
Pour connaître l'angle entre les lignes, deux vecteurs sont nécessaires ou alors Oui v qui appartiennent à chacun d'eux. Ainsi, il est possible de connaître l'angle qu'ils forment au moyen du produit scalaire des vecteurs, défini de cette manière:
ou alors•v =u.v.cos α
Équation de la ligne dans le plan
Une ligne dans le plan cartésien peut être représentée de plusieurs manières, telles que:
-Forme d'interception de pente: Oui m est la pente de la ligne et b est l'intersection de la ligne avec l'axe vertical, l'équation de la ligne est y = mx + b.
-Équation générale pour une ligne droite: Axe + Par + C = 0, où m = A / B est la pente.
Dans le plan cartésien, les lignes verticales et horizontales sont des cas particuliers de l'équation de la ligne.
-Lignes verticales: x = a
-Lignes horizontales: y = k
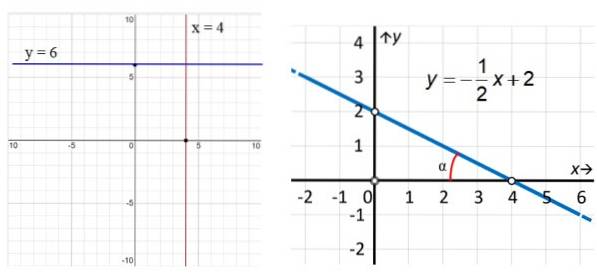
Dans les exemples de la figure 3, la ligne verticale rouge a l'équation x = 4, tandis que la ligne parallèle à l'axe x (bleu) a l'équation y = 6. Quant à la ligne de droite, on voit qu'elle est oblique et à trouver son équation nous utilisons les points mis en évidence dans la figure: (0,2) et (4,0) de cette façon:
m = (etdeux - Oui1) / (Xdeux - X1) = (2 - 0) / (0 - 4) = - ½
La coupe de cette ligne avec l'axe vertical est y = 2, comme on peut le voir sur le graphique. Avec ces informations:
y = (-½) x + 2
La détermination de l'angle d'inclinaison par rapport à l'axe x est facile. Je sens ça:
α = arcg (2/4) = 26,6 °
Par conséquent, l'angle positif de l'axe x à la ligne est: 180 ° - 26,6 ° = 153,4 °
Exemples de lignes obliques

Des lignes obliques apparaissent à de nombreux endroits, il s'agit de faire attention à les retrouver dans l'architecture, les sports, les câblages électriques, les tuyaux et bien d'autres endroits. Dans la nature, des lignes obliques sont également présentes, comme nous le verrons ci-dessous:
Rayons de lumière
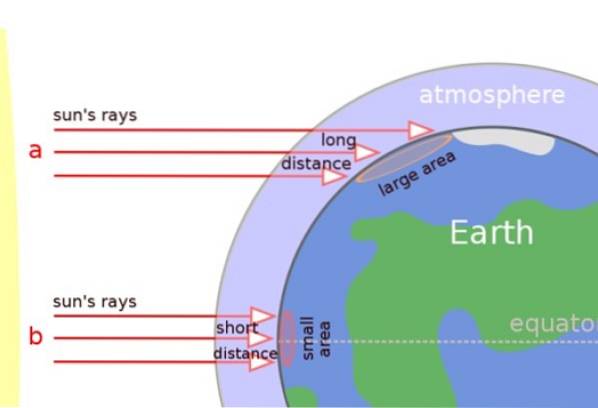
La lumière du soleil se déplace en ligne droite, mais la forme arrondie de la Terre affecte la façon dont la lumière du soleil frappe la surface..
Dans l'image ci-dessous, nous pouvons clairement voir que les rayons du soleil frappent perpendiculairement dans les régions tropicales, mais atteignent plutôt obliquement la surface dans les régions tempérées et aux pôles..
C'est pourquoi les rayons du soleil parcourent une plus longue distance à travers l'atmosphère et la chaleur se propage également sur une plus grande surface (voir figure). Le résultat est que les zones proches des pôles sont plus froides.
Lignes qui ne sont pas dans le même plan
Lorsque deux lignes ne sont pas dans le même plan, elles peuvent toujours être obliques ou voilé, comme ils sont également connus. Dans ce cas, leurs vecteurs directeurs ne sont pas parallèles, mais comme ils n'appartiennent pas au même plan, ces lignes ne se croisent pas.
Par exemple, les lignes de la figure 6 à droite sont clairement sur des plans différents. Si vous les regardez d'en haut, vous pouvez voir qu'ils se croisent effectivement, mais ils n'ont pas de point commun. Sur la droite, nous voyons les roues du vélo, dont les rayons semblent se croiser vu de face.

Les références
- Géométrie. Vecteur directeur d'une ligne. Récupéré de: juanbragado.es.
- Larson, R. 2006. Calcul avec géométrie analytique. 8ème. Édition. Mcgraw Hill.
- Les mathématiques sont un jeu. Lignes et angles. Récupéré de: juntadeandalucia.es.
- Des lignes droites qui se croisent. Récupéré de: profesoraltuna.com.
- Villena, M. Géométrie analytique en R3. Récupéré de: dspace.espol.edu.ec.


Personne n'a encore commenté ce post.