
Concept des réseaux Bravais, caractéristiques, exemples, exercices
le Filets Bravais Ils sont l'ensemble de quatorze cellules unitaires tridimensionnelles dans lesquelles les atomes d'un cristal peuvent être localisés. Ces cellules consistent en un agencement tridimensionnel de points qui forment une structure de base qui se répète périodiquement dans les trois directions spatiales..
L'origine de cette dénomination pour les structures cristallines de base vient de 1850, quand Auguste Bravais a montré qu'il n'y avait que 14 cellules unitaires de base tridimensionnelles possibles.

L'ensemble des 14 réseaux Bravais sont subdivisés en sept groupes ou structures selon la géométrie des cellules, ces sept groupes sont:
1- cubique
2- Tétragonale
3- Orthorhombique
4- Trigonal-Hexagonal
5- Monoclinique
6- Triclinique
7- Trigonal
Chacune de ces structures définit une cellule unitaire, c'est la plus petite partie qui préserve la disposition géométrique des atomes dans le cristal..
Index des articles
- 1 Caractéristiques des réseaux Bravais
- 1.1 Réseaux cubiques
- 2 exemples
- 2.1 - Fer
- 2.2 - Cuivre
- 2.3 - Gemmes précieuses
- 2.4 Topaze
- 3 exercices résolus
- 3.1 Exercice 1
- 3.2 Exercice 2
- 3.3 Exercice 3
- 4 Références
Caractéristiques des réseaux Bravais
Les quatorze réseaux Bravais, comme mentionné ci-dessus, sont subdivisés en sept groupes. Mais chacun de ces groupes a ses cellules unitaires avec ses paramètres caractéristiques qui sont:
1- Le paramètre réseau (a, b, c)
2- Nombre d'atomes par cellule
3- Relation entre le paramètre de réseau et le rayon atomique
4- Numéro de coordination
5- Facteur d'emballage
6- espaces interstitiels
7- Grâce aux traductions le long des vecteurs a, b, c la structure cristalline est répétée.
Réseaux cubiques
Il se compose du réseau cubique ou cubique simple P, du réseau cubique à faces centrées ou réseau cubique F et du réseau cubique centré sur le corps ou réseau cubique I.
Tous les réseaux cubiques ont les trois paramètres de réseau correspondant aux directions x, y, z de même valeur:
a = b = c
Réseau cubique P
Il est à noter que les atomes sont représentés par des sphères dont les centres sont aux sommets de la cellule unitaire cubique P.
Dans le cas du réseau cubique P, le nombre d'atomes par cellule est égal à 1, car à chaque sommet, seul un huitième de l'atome se trouve à l'intérieur de la cellule unitaire, donc 8 * ⅛ = 1.
le numéro de coordination indique le nombre d'atomes qui sont proches voisins dans le réseau cristallin. Dans le cas du réseau cubique P, le nombre de coordination est 6.
Réseau cubique I
Dans ce type de réseau, en plus des atomes aux sommets du cube, il y a un atome au centre du cube. Alors le nombre d'atomes par cellule l'unité dans le réseau cubique P est 2 atomes.

Réseau cubique F
C'est le réseau cubique qui, en plus des atomes dans les sommets, a un atome au centre de la face de chaque cube. le nombre d'atomes par cellule est 4, puisque chacun des six atomes de la face a la moitié à l'intérieur de la cellule, c'est-à-dire 6 * ½ = 3 plus 8 * ⅛ = 1 aux sommets.

Filet hexagonal
Dans ce cas, la maille élémentaire est un prisme droit à base hexagonale. Les réseaux hexagonaux ont les trois paramètres de réseau correspondant remplissant la relation suivante:
a = b ≠ c
L'angle entre les vecteurs a et b étant de 120 °, comme indiqué sur la figure. Alors qu'entre les vecteurs a et c, ainsi qu'entre b et c, des angles droits se forment.

le nombre d'atomes par cellule sera calculé comme suit:
- Dans chacune des 2 bases du prisme hexagonal, il y a 6 atomes aux six sommets. Chacun de ces atomes occupe les ⅙ de la maille élémentaire.
- Au centre de chacune des 2 bases hexagonales, il y a 1 atome qui occupe 1/2 cellule unitaire.
- Sur les 6 faces latérales du prisme hexagonal, il y a 3 atomes occupant chacun ⅔ de la maille élémentaire, et 3 atomes occupant chacun ⅓ du volume de la maille élémentaire.
(6 x ⅙) x 2 + ½ x 2 + ⅔ x 3 + ⅓ x 3 = 6
La relation entre les paramètres de réseau a et b avec le rayon atomique R sous l'hypothèse que tous les atomes sont de rayon égal et sont en contact est:
a / R = b / R = 2
Exemples
Les métaux sont les principaux exemples de structures cristallines et aussi les plus simples car ils sont généralement constitués d'un seul type d'atome. Mais il existe d'autres composés non métalliques qui forment également des structures cristallines, telles que le diamant, le quartz et bien d'autres..
- Le fer
Le fer a une seule cellule unitaire cubique avec un paramètre de réseau ou de bord a = 0,297 nm. Dans 1 mm, il y a 3,48 x 10 ^ 6 cellules unitaires.
- Le cuivre
Il a une structure cristalline cubique à faces centrées, composée uniquement d'atomes de cuivre..
- Gemmes précieuses
Les pierres précieuses sont des structures cristallines essentiellement du même composé, mais avec de petites portions d'impuretés qui sont souvent responsables de leur couleur..
diamant
Il est composé uniquement de carbone et ne contient pas d'impuretés, c'est pourquoi il est incolore. Le diamant a structure cristalline cubique (isométrique-hexoctaédrique) et est le matériau le plus dur connu.
Quartz
Il est composé d'oxyde de silice, il est généralement incolore ou blanc. Sa structure cristalline est trigonale-trapézoédrique.
Rubis
Il est composé d'oxyde d'aluminium avec des impuretés de chrome qui lui donnent sa couleur rouge caractéristique. Formez un réseau cristallin hexagonal.
Saphir
C'est aussi un cristal d'oxyde d'aluminium, mais avec des impuretés de titane et de fer, qui sont responsables de sa couleur bleue dans diverses nuances. Comme le rubis a structure hexagonale.
Jade
Gemme généralement de couleur verte, a structure monoclinique et est composé de silicate de fer-magnésium-calcium.
Topaze
Il est incolore avec un structure orthorhombique fluorure-hydroxyde-silicate d'aluminium.
Exercices résolus
Exercice 1
Trouvez la relation entre le paramètre de réseau et le rayon atomique pour un réseau cubique F.
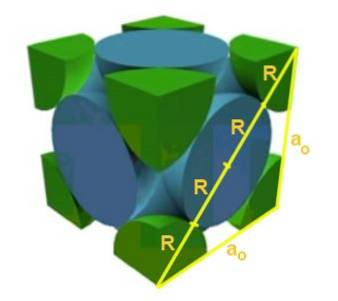
Solution: Tout d'abord, on suppose que les atomes sont représentés comme des sphères de rayon R toutes en "contact" les unes avec les autres, comme le montre la figure. Un triangle rectangle se forme dans lequel il est vrai que:
(4 R) ^ 2 = a ^ 2 + a ^ 2 = 2 a ^ 2
Par conséquent, la relation arête-rayon est:
a / R = 4 / √2
Exercice 2
Trouvez la relation entre le paramètre de réseau et le rayon atomique pour un réseau cubique I (centré sur le corps).
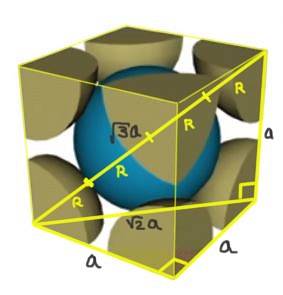
Solution: Les atomes sont censés être représentés comme des sphères de rayon R toutes en "contact" les unes avec les autres, comme le montre la figure.
Deux triangles rectangles sont formés, l'un de l'hypoténuse √2a et l'autre de l'hypoténuse √3a comme on peut le prouver en utilisant le théorème de Pythagore. De là, il s'ensuit que la relation entre le paramètre de réseau et le rayon atomique pour un réseau cubique I (centré dans le corps) est:
a / R = 4 / √3
Exercice 3
Trouvez le facteur d'emballage F pour une maille élémentaire d'une structure cubique F (face centrée cubique) dans laquelle les atomes ont un rayon R et sont en "contact".
Solution: Le facteur d'emballage F est défini comme le quotient entre le volume occupé par les atomes dans la maille élémentaire et le volume de la maille:
F = Vles atomes / Vcellule
Comme démontré ci-dessus, le nombre d'atomes par maille unitaire dans un réseau cubique à faces centrées est de 4, donc le facteur d'emballage sera:
F = 4 [4πR ^ 3/3] / [a ^ 3] =…
… 4 [4πR ^ 3/3] / [4R / √2] ^ 3 = (√2) π / 6 = 0,74
Les références
- Centre de ressources académiques Crystal Structures. [PDF]. Extrait le 24 mai 2018 de: web.iit.edu
- Cristaux. Récupéré le 26 mai 2018 de: thinkco.com
- Pressbooks. 10.6 Structures en treillis dans les solides cristallins. Extrait le 26 mai 2018 de: opentextbc.ca
- Ming. (2015, 30 juin). Types de structures cristallines. Récupéré le 26 mai 2018 de: crystalvisions-film.com
- Helmenstine, Anne Marie, Ph.D. (31 janvier 2018). Types de
- Kittel Charles (2013) Physique du solide, Physique de la matière condensée (8e édition). Wiley.
- KHI. (2007). Structures cristallines. Extrait le 26 mai 2018 de: folk.ntnu.no
- Wikipédia. Treillis de Bravais. Récupéré de: en.wikipedia.com.



Personne n'a encore commenté ce post.