
Méthode graphique de soustraction de vecteurs, exemples, exercices
La soustraction vectorielle ou soustraction vectorielle entre vecteurs ou alors Oui v désigné par ou alors - v, est calculé en ajoutant le vecteur ou alors avec le vecteur ci-contre v. Algébriquement, la soustraction est exprimée comme suit:
ou alors - v = ou alors + (-v)
Il est possible d'effectuer une soustraction vectorielle en suivant diverses procédures, par exemple graphiquement, de cette manière un vecteur v est dessinée par un segment de ligne orienté - une flèche-.
La longueur de la flèche correspond au module du vecteur, l'inclinaison - par rapport à une ligne de référence donnée - indique la direction et la fin indique la direction du vecteur.
Le vecteur opposé v il a la même longueur et la même direction, mais la direction opposée. Ensuite, avant de faire la soustraction entre ou alors Oui v, il faut dessiner le vecteur ci-contre v, et ajoutez ce vecteur à u.
Il est très important de noter que la soustraction vectorielle n'est pas commutative, c'est-à-dire que l'ordre des vecteurs modifie le résultat, donc:
ou alors - v ≠ v - ou alors
La procédure graphique peut être réalisée en utilisant l'une de ces méthodes, dont nous expliquerons ci-dessous les étapes:
-Méthode du triangle.
-Méthode du parallélogramme.
Index des articles
- 1 Méthode graphique de soustraction vectorielle
- 1.1 Méthode du triangle
- 1.2 Méthode du parallélogramme
- 2 Exemples de soustraction vectorielle
- 2.1 - Exemple 1
- 2.2 - Exemple 2
- 3 Exercice résolu
- 3.1 Solution
- 4 Références
Méthode de soustraction vectorielle graphique
Méthode du triangle
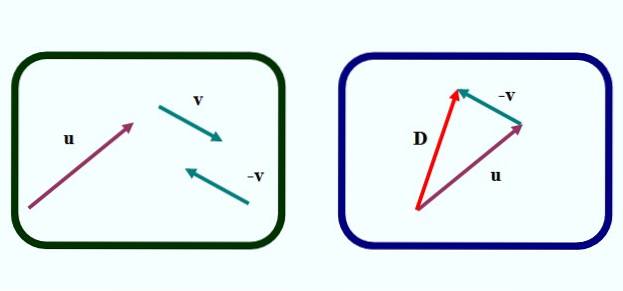
Dans la figure 1, nous avons la première des méthodes pour soustraire graphiquement deux vecteurs. Il s'agit de méthode du triangle, car la figure qui se forme en établissant les vecteurs est un triangle, comme on peut le voir sur l'image de gauche.
Pour faire la soustraction ou alors - v nous procédons comme suit:
-Dessinez le vecteur -v du vecteur v, par translation avec une règle et un carré, mais en changeant le sens de la flèche (image de gauche).
-Passe au vecteur -v de telle manière que son origine coïncide avec la fin du vecteur ou alors (image de droite).
-Ensuite, un vecteur est dessiné (en rouge dans l'image de droite) qui part de l'origine de ou alors à la fin de v. Appel ré y est le vecteur de différence:
ré = ou alors - v
Méthode du parallélogramme
Dans la méthode du parallélogramme, les vecteurs à ajouter ou à soustraire doivent coïncider à leurs points d'origine. Supposons que nous voulions trouver ou alors - v Avec nos vecteurs illustrés ci-dessus, les étapes pour trouver la soustraction de vecteurs par cette méthode sont les suivantes:
-Déterminez le vecteur opposé v, Qu'est que c'est -v, comme décrit ci-dessus pour la méthode du triangle.
-Traduisez soigneusement les vecteurs ou alors Oui -v de telle manière que leurs origines coïncident.
-Des lignes parallèles segmentées sont maintenant dessinées à partir des extrémités de chaque vecteur. La figure qui se forme est un parallélogramme et dans les cas particuliers où les vecteurs sont perpendiculaires, il en résulte un rectangle ou un carré..
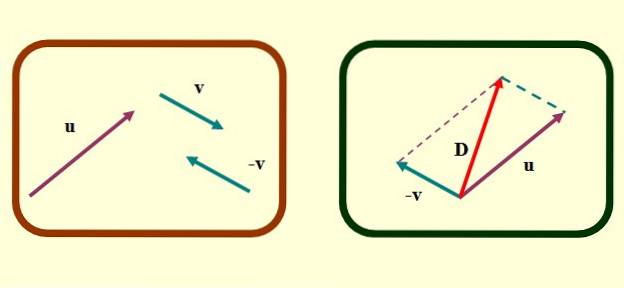
-Enfin, un vecteur est dessiné qui part de l'origine commune de ou alors Oui v à l'extrême où les lignes parallèles segmentées se croisent. C'est le vecteur ré ou soustraction.
Important
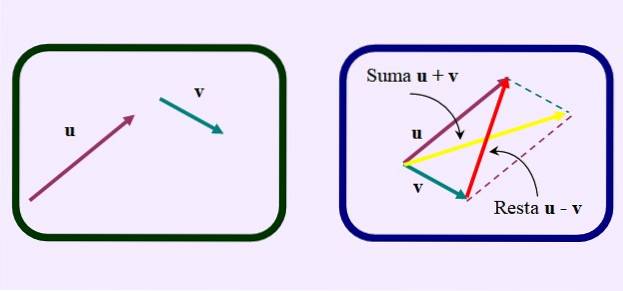
Une autre façon de faire la soustraction consiste à dessiner le parallélogramme comme si vous vouliez ajouter les vecteurs.
Mais au lieu de dessiner la diagonale habituelle de la somme, qui va de l'origine commune à l'intersection des parallèles, le diagonale opposée ou plus courte, comme le montre la figure:
Exemples de soustraction vectorielle
- Exemple 1
Un navire navigue sur une rivière et le fait dans la direction opposée au courant. Un observateur à terre constate que la vitesse du bateau est réduite en raison de l'action du courant.
La vitesse est un vecteur et dans cet exemple, la vitesse du bateau pointe dans une direction et la vitesse du courant a la même direction et direction opposée. La vitesse nette du navire est la somme des deux vecteurs.
Par exemple, si les instruments du bateau indiquent qu'il se déplace à v '= + 40 km / h et qu'un observateur à terre mesure que le bateau se déplace à v = + 30 km / h. Puisque v = v '+ Vc, où Vc est la vitesse du courant qui est calculée en soustrayant respectivement les vitesses v et v': Vc = v - v '= 30 km / h - 40 km / h = -10 km / h.
- Exemple 2
En cinématique, nous avons des vecteurs importants qui décrivent les changements:
-Décalage pour les changements de position.
-Vitesse moyenne, pour quantifier la vitesse à laquelle la position varie dans le temps.
-Accélération, pour les changements de vitesse en fonction du temps.
Le vecteur de déplacement
Le vecteur de déplacement décrit le changement de position qu'un corps subit au cours de son mouvement.
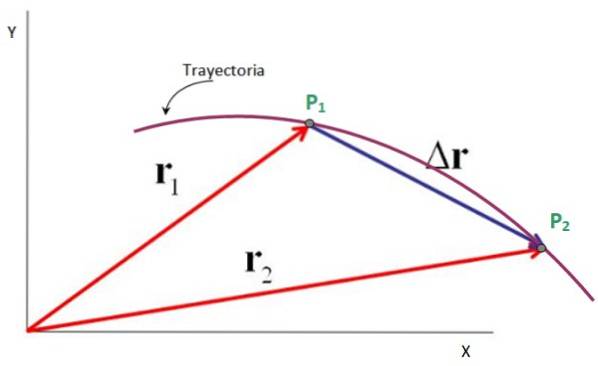
Voyons par exemple une particule qui décrit la trajectoire plane représentée sur la figure, dans laquelle elle passe du point P1 au point Pdeux.
Les vecteurs dirigés de l'origine du repère x-y vers ces points sont les vecteurs de position r1 Oui rdeux, tandis que le vecteur de déplacement est Δr, qui va de P1 Hautdeux. C'est vrai que:
Δr = rdeux - r1
Par conséquent, le vecteur de déplacement est la soustraction entre le vecteur de position finale et le vecteur de position initiale, comme le montre la figure suivante. Ses unités sont aussi celles de position: mètres, pieds, miles, centimètres et plus..
Les vecteurs de vitesse moyenne et d'accélération moyenne
Pour sa part, le vecteur vitesse moyenne vm est défini comme le décalage multiplié par l'inverse de l'intervalle de temps:


Exercice résolu
Une particule qui décrit un cercle met 5 s pour passer du point A au point B.En A, elle a une vitesse vÀ = 60 km / h vers l'axe + x et en B est vB = 60 km / h vers + y. Déterminer son accélération moyenne graphiquement et analytiquement.
Solution
Sous forme graphique, la direction et la direction de l'accélération moyenne sont déterminées par:

Dans l'image suivante se trouve la soustraction vB - vÀ, en utilisant la méthode du triangle, puisque l'accélération moyenne àm est proportionnel à Δv. Le triangle formé a les deux jambes égales et donc les angles internes aigus mesurent 45º chacun..

Analytiquement, si la direction + x coïncide avec le vecteur unitaire je et la direction + y avec le vecteur unitaire j, ensuite:
Δv = 60 km / h j - 60 km / h je
En prenant Δt = 5 s, selon les informations de l'énoncé, l'accélération moyenne est:
àm = (60 km / h j - 60 km / h je) / 5 s = 12 (j-je) km / (h.s)
Les références
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
- Bedford, 2000. A. Mécanique du génie: statique. Addison Wesley.
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Edité par Douglas Figueroa (USB).
- Giambattista, A. 2010. Physique. 2ème. Ed. McGraw Hill.
- Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 1.
- Tipler, P. 2006. Physique pour la science et la technologie. 5e éd. Volume 1. Éditorial Reverté.


Personne n'a encore commenté ce post.