La symétrie axiale Il se produit lorsque les points d'une figure coïncident avec les points d'une autre figure au moyen d'une bissectrice droite appelée axe de symétrie. Elle est également appelée symétrie radiale, rotationnelle ou cylindrique..
Il est généralement appliqué sous forme de figures géométriques, mais il est facilement observable dans la nature, car il existe des animaux tels que des papillons, des scorpions, des coccinelles ou des humains qui présentent une symétrie axiale..
Index des articles
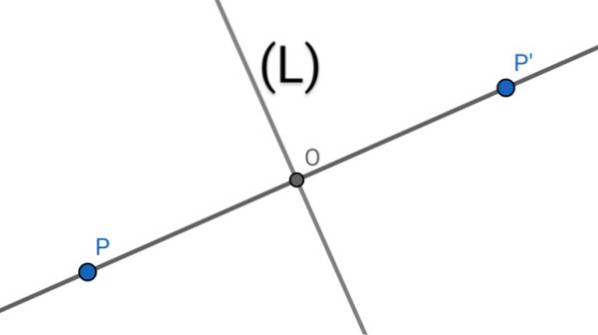
Pour trouver la symétrie axiale P 'd'un point P par rapport à une droite (L), les opérations géométriques suivantes sont effectuées:
1.- La perpendiculaire à la droite (L) qui passe par le point P est dessinée.
2.- L'interception des deux lignes détermine un point O.
3.- La longueur du segment PO est mesurée, puis cette longueur est recopiée sur la ligne (PO) à partir de O dans le sens de P vers O déterminant le point P '.
4.- Le point P 'est la symétrie axiale du point P par rapport à l'axe (L), puisque la droite (L) est la médiatrice du segment PP', où O est le milieu dudit segment.
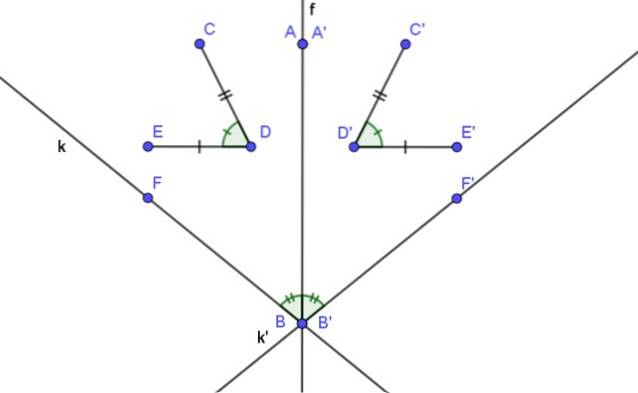
- La symétrie axiale est isométrique, c'est-à-dire que les distances d'une figure géométrique et sa symétrie correspondante sont conservées.
- La mesure d'un angle et celle de son symétrique sont égales.
- La symétrie axiale d'un point sur l'axe de symétrie est le point lui-même.
- La ligne symétrique d'une ligne parallèle à l'axe de symétrie est également une ligne parallèle audit axe.
- Une ligne sécante à l'axe de symétrie a comme ligne symétrique une autre ligne sécante qui, à son tour, coupe l'axe de symétrie au même point de la ligne d'origine.
- L'image symétrique d'une ligne est une autre ligne qui forme un angle avec l'axe de symétrie de la même mesure que celle de la ligne d'origine.
- L'image symétrique d'une ligne perpendiculaire à l'axe de symétrie est une autre ligne qui chevauche la première.
- Une ligne et sa ligne symétrique axiale forment un angle dont la bissectrice est l'axe de symétrie.
La nature présente de nombreux exemples de symétrie axiale. Par exemple, vous pouvez voir la symétrie des visages, des insectes tels que les papillons, la réflexion sur les surfaces d'eau calmes et les miroirs ou les feuilles des plantes, entre autres..
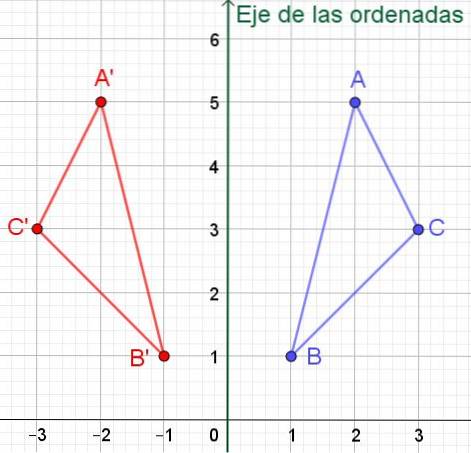
On a le triangle des sommets A, B et C dont les coordonnées cartésiennes sont respectivement A = (2, 5), B = (1, 1) et C = (3,3). Trouvez les coordonnées cartésiennes du triangle symétrique par rapport à l'axe Y (axe des ordonnées).
Solution: Si un point P a des coordonnées (x, y) alors sa symétrie par rapport à l'axe des ordonnées (axe Y) est P '= (- x, y). Autrement dit, la valeur de son abscisse change de signe, tandis que la valeur de l'ordonnée reste la même.
Dans ce cas, le triangle symétrique de sommets A ', B' et C 'aura les coordonnées:
A '= (- 2, 5); B '= (- 1, 1) et C' = (- 3, 3) comme le montre la figure 6.
En référence au triangle ABC et à son A'B'C 'symétrique de l'exercice 1, vérifier que les côtés correspondants du triangle d'origine et sa symétrique ont la même longueur.
Solution: Pour trouver la distance ou la longueur des côtés, nous utilisons la formule de distance euclidienne:
d (A, B) = √ ((Bx - Ax) ^ 2 + (Par - Ay) ^ 2) = √ ((1-2) ^ 2 + (1-5) ^ 2) = √ ((- 1 ) ^ 2 + (-4) ^ 2) = √ (17) = 4,123
La longueur du côté symétrique A'B 'correspondant est calculée ci-dessous:
d (A ', B') = √ ((Bx'-Axe ') ^ 2 + (Par'-Ay') ^ 2) = √ ((- 1 + 2) ^ 2 + (1-5) ^ 2 ) = √ ((1) ^ 2 + (-4) ^ 2) = √ (17) = 4,123
De cette manière, on vérifie que la symétrie axiale préserve la distance entre deux points. La procédure peut être répétée pour les deux autres côtés du triangle et son symétrique pour vérifier l'invariance de longueur. Par exemple | AC | = | A'C '| = √5 = 2 236.
Par rapport au triangle ABC et à son A'B'C 'symétrique de l'exercice 1, vérifier que les angles correspondants du triangle d'origine et de son symétrique ont la même mesure angulaire.
Solution: Pour déterminer les mesures des angles BAC et B'A'C ', le produit scalaire des vecteurs sera d'abord calculé UN B avec AC puis le produit scalaire de UN B ' avec A'C '.
En se rappelant que:
A = (2, 5), B = (1, 1) et C = (3,3)
A '= (- 2, 5); B '= (- 1, 1) et C' = (- 3, 3).
Il a:
UN B = <1-2, 1-5> Oui AC = <3-2, 3-5>
De même
UN B ' = <-1+2, 1-5> Oui AC = <-3+2, 3-5>
Ensuite, les produits scalaires suivants sont trouvés:
AB⋅AC = <-1, -4>⋅<1, -2> = -1⋅1 + (-4) ⋅ (-2) = -1 + 8 = 7
De même
A'B'⋅A'C ' = <1, -4>⋅<-1, -2> = 1⋅ (-1) + (-4) ⋅ (-2) = -1 + 8 = 7
La mesure de l'angle BAC est:
∡BAC = ArcCos ( AB⋅AC / (|AB |⋅ |AC |)) =
ArcCos (7 / (4 123⋅2 236)) = 40,6 °
De même, la mesure de l'angle B'A'C 'est:
∡B'A'C '= ArcCos ( A'B'⋅A'C ' / (|A'B '|⋅ |A'C '|)) =
ArcCos (7 / (4 123⋅2 236)) = 40,6 °
Conclusion que la symétrie axiale préserve la mesure d'angle.
Soit un point P de coordonnées (a, b). Trouver les coordonnées de sa symétrie axiale P 'par rapport à la droite y = x.
Solution: On appellera (a ', b') les coordonnées du point symétrique P 'par rapport à la droite y = x. Le milieu M du segment PP 'a les coordonnées ((a + a') / 2, (b + b ') / 2) et est également sur la ligne y = x, donc l'égalité suivante est vraie:
a + a '= b + b'
Par contre, le segment PP 'a la pente -1 car il est perpendiculaire à la droite y = x avec la pente 1, donc l'égalité suivante est vraie:
b - b '= a' -a
En résolvant les deux égalités précédentes a 'et b', on conclut que:
a '= b et que b' = a.
Autrement dit, étant donné un point P (a, b), sa symétrie axiale par rapport à la droite y = x est P '(b, a).
Personne n'a encore commenté ce post.