
Théorème de Chebyshov ce que c'est, applications et exemples
le Théorème de Chebyshov (ou l'inégalité de Chebyshov) est l'un des résultats classiques les plus importants de la théorie des probabilités. Il permet d'estimer la probabilité d'un événement décrit en termes de variable aléatoire X, en nous fournissant une borne qui ne dépend pas de la distribution de la variable aléatoire mais de la variance de X.
Le théorème est nommé d'après le mathématicien russe Pafnuty Chebyshov (également écrit comme Chebychev ou Tchebycheff) qui, bien qu'il n'ait pas été le premier à énoncer le théorème, a été le premier à donner une preuve en 1867.

Cette inégalité, ou celles qui, en raison de leurs caractéristiques, sont appelées inégalité de Chebyshov, est principalement utilisée pour approximer les probabilités en calculant des bornes.
Index des articles
- 1 Qu'est-ce que?
- 2 Applications et exemples
- 2.1 Limitation des probabilités
- 2.2 Preuve des théorèmes limites
- 2.3 Taille de l'échantillon
- 3 Inégalités de type Chebyshov
- 4 Références
En quoi consiste?
Dans l'étude de la théorie des probabilités, il arrive que si la fonction de distribution d'une variable aléatoire X est connue, sa valeur attendue - ou espérance mathématique E (X) - et sa variance Var (X) peuvent être calculées, tant que de tels montants existent . Cependant, l'inverse n'est pas nécessairement vrai..
Autrement dit, connaissant E (X) et Var (X), il n'est pas nécessairement possible d'obtenir la fonction de distribution de X, donc des quantités telles que P (| X |> k) pour certains k> 0 sont très difficiles à obtenir. Mais grâce à l'inégalité de Chebyshov, il est possible d'estimer la probabilité de la variable aléatoire.
Le théorème de Chebyshov nous dit que si nous avons une variable aléatoire X sur un espace échantillon S avec une fonction de probabilité p, et si k> 0, alors:
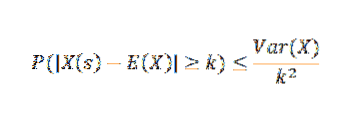
Applications et exemples
Parmi les nombreuses applications du théorème de Chebyshov, on peut citer les suivantes:
Limiter les probabilités
C'est l'application la plus courante et est utilisée pour donner une borne supérieure pour P (| X-E (X) | ≥k) où k> 0, uniquement avec la variance et l'espérance de la variable aléatoire X, sans connaître la fonction de probabilité.
Exemple 1
Supposons que le nombre de produits fabriqués dans une entreprise pendant une semaine soit une variable aléatoire avec une moyenne de 50.
Si l'on sait que la variance d'une semaine de production est égale à 25, alors que pouvons-nous dire de la probabilité que cette semaine la production diffère de plus de 10 de la moyenne?
Solution
En appliquant l'inégalité de Chebyshov, nous avons:
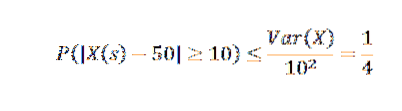
À partir de là, nous pouvons obtenir que la probabilité que dans la semaine de production le nombre d'articles dépasse la moyenne de plus de 10 est au plus 1/4.
Preuve des théorèmes des limites
L'inégalité de Chebyshov joue un rôle important dans la démonstration des théorèmes limites les plus importants. À titre d'exemple, nous avons les éléments suivants:
Loi faible des grands nombres
Cette loi établit que pour une suite X1, X2,…, Xn,… de variables aléatoires indépendantes de même distribution moyenne E (Xi) = μ et variance Var (X) = σdeux, et un échantillon moyen connu de:
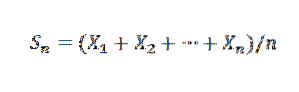
Alors pour k> 0 on a:
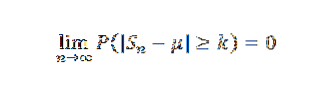
Ou équivalent:
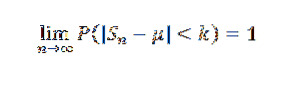
Manifestation
Remarquons d'abord ce qui suit:
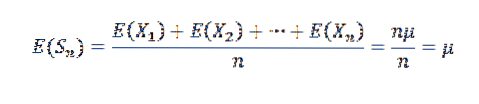
Puisque X1, X2,…, Xn sont indépendants, il s'ensuit que:
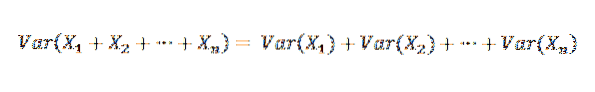
Par conséquent, il est possible de déclarer ce qui suit:
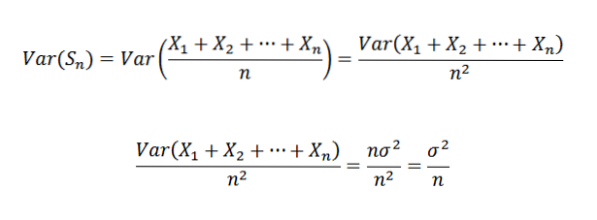
Ensuite, en utilisant le théorème de Chebyshov, nous avons:
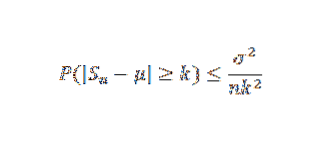
Enfin, le théorème résulte du fait que la limite à droite est nulle lorsque n tend vers l'infini.
Il est à noter que ce test n'a été fait que pour le cas où la variance de Xi existe; c'est-à-dire qu'il ne diverge pas. On observe donc que le théorème est toujours vrai si E (Xi) existe.
Théorème limite de Chebyshov
Si X1, X2,…, Xn,… est une suite de variables aléatoires indépendantes telle qu'il y ait un certain C< infinito, tal que Var(Xn) ≤ C para todo n natural, entonces para cualquier k>0:
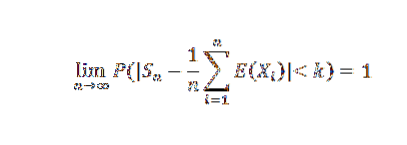
Manifestation
Puisque la séquence des variances est uniformément bornée, nous avons que Var (Sn) ≤ C / n, pour tout n naturel. Mais nous savons que:
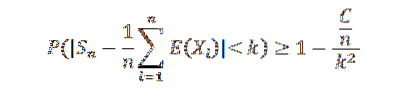
Faire tendre n vers l'infini, les résultats suivants:
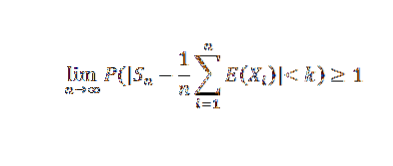
Puisqu'une probabilité ne peut pas dépasser la valeur de 1, le résultat souhaité est obtenu. Comme conséquence de ce théorème, nous pourrions citer le cas particulier de Bernoulli.
Si un experimento se repite n veces de forma independiente con dos resultados posibles (fracaso y éxito), donde p es la probabilidad de éxito en cada experimento y X es la variable aleatoria que representa el número de éxitos obtenidos, entonces para cada k>0 il faut que:
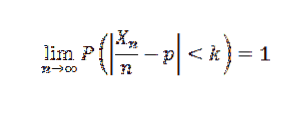
Taille de l'échantillon
En termes de variance, l'inégalité de Chebyshov nous permet de trouver une taille d'échantillon n suffisante pour garantir que la probabilité que | Sn-μ |> = k se produise soit aussi faible que souhaité, ce qui nous permet d'avoir une approximation de la moyenne.
Précisément, soit X1, X2,… Xn un échantillon de variables aléatoires indépendantes de taille n et supposons que E (Xi) = μ et sa variance σdeux. Ainsi, par l'inégalité de Chebyshov, nous avons:
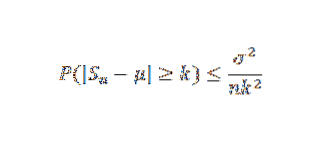
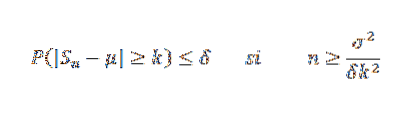
Exemple
Supposons que X1, X2,… Xn sont un échantillon de variables aléatoires indépendantes de distribution de Bernoulli, telles qu'elles prennent la valeur 1 avec une probabilité p = 0,5.
Quelle devrait être la taille de l'échantillon pour pouvoir garantir que la probabilité que la différence entre la moyenne arithmétique Sn et sa valeur attendue (dépassant de plus de 0,1) soit inférieure ou égale à 0., 01?
Solution
On a que E (X) = μ = p = 0,5 et que Var (X) = σdeux= p (1-p) = 0,25. Par l'inégalité de Chebyshov, pour tout k> 0 on a:
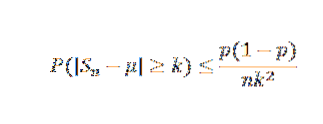
Maintenant, en prenant k = 0,1 et δ = 0,01, nous avons:
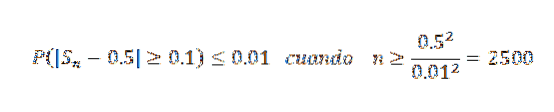
De cette manière, on conclut qu'une taille d'échantillon d'au moins 2500 est nécessaire pour garantir que la probabilité de l'événement | Sn - 0,5 |> = 0,1 est inférieure à 0,01.
Inégalités de type Chebyshov
Il existe plusieurs inégalités liées à l'inégalité de Chebyshov. L'une des plus connues est l'inégalité de Markov:
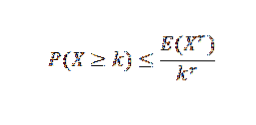
Dans cette expression, X est une variable aléatoire non négative avec k, r> 0.
L'inégalité de Markov peut prendre différentes formes. Par exemple, soit Y une variable aléatoire non négative (donc P (Y> = 0) = 1) et supposons que E (Y) = μ existe. Supposons aussi que (E (Y))r= μr existe pour un entier r> 1. Ensuite:
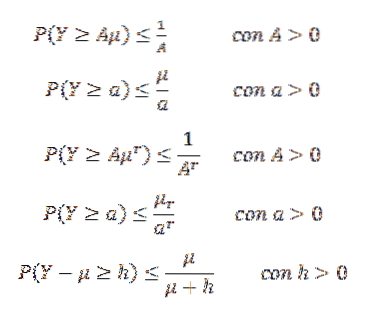
Une autre inégalité est gaussienne, ce qui nous dit que étant donné une variable aléatoire unimodale X avec mode à zéro, alors pour k> 0,
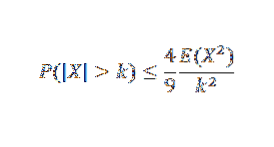
Les références
- Kai Lai Chung. Théorie élémentaire de la rentabilité avec des processus stochastiques. Springer-Verlag New York Inc
- Kenneth.H. Rosen: Mathématiques discrètes et ses applications. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Probabilité et applications statistiques. S.A. ALHAMBRA MEXICAIN.
- Seymour Lipschutz Ph.D. 2000 Problèmes résolus de mathématiques discrètes. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Problèmes de théorie et de probabilité. McGRAW-HILL.



Personne n'a encore commenté ce post.