
Théorème, preuve, applications et exercices de Green
le Théorème de Green est une méthode de calcul utilisée pour relier les intégrales de ligne à des intégrales à double surface ou à surface. Les fonctions impliquées doivent être désignées comme des champs vectoriels et définies dans le chemin C.
Par exemple, une expression intégrale de ligne peut être très difficile à résoudre; cependant, en implémentant le théorème de Green, les doubles intégrales deviennent assez basiques. Il est toujours important de respecter le sens positif de la trajectoire, cela se réfère au sens anti-horaire.

Le théorème de Green est un cas particulier du théorème de Stokes, où la projection de la fonction vectorielle est effectuée dans le plan xy.
Index des articles
- 1 Définition
- 2 Démo
- 3 applications
- 4 Histoire
- 5 Relation avec d'autres théorèmes
- 6 exercices
- 7 Références
Définition
L'expression du théorème de Green est la suivante:
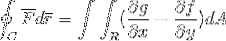
Le premier terme montre l'intégrale de ligne définie par le chemin «C», du produit scalaire entre la fonction vectorielle «F» et celle du vecteur «r».
C: C'est le chemin défini sur lequel la fonction vectorielle sera projetée tant qu'elle est définie pour ce plan.
F: fonction vectorielle, où chacun de ses composants est défini par une fonction comme telle (f, g).
r: C'est un vecteur tangent à la région R sur laquelle l'intégrale est définie. Dans ce cas on opère avec un différentiel de ce vecteur.
Dans le second terme, nous voyons le théorème de Green développé, où la double intégrale définie dans la région R de la différence des dérivées partielles de g et f, par rapport à x et y respectivement, est observée. Par un différentiel de surface qui n'est rien de plus que le produit des deux différentiels bidimensionnels (dx.dy).
Ce théorème est parfaitement applicable pour les intégrales spatiales et surfaciques.
Manifestation
Pour prouver le théorème de Green de manière simple, cette tâche sera décomposée en 2 parties. Nous supposerons d'abord que la fonction vectorielle F n'a de définition que dans le verseur je. Alors que la fonction "g" correspondant au verseur j sera égal à zéro.
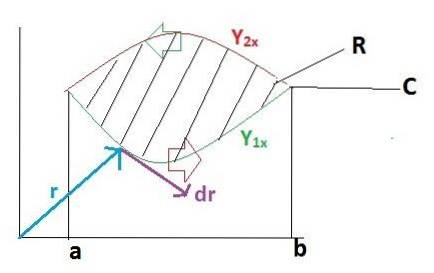
F = f (x, y)je + g (x, y)j = f (x, y)je + 0
r = xje + Ouij
dr = dxje + mourirj
Nous développons d'abord l'intégrale de ligne sur la trajectoire C, pour laquelle la trajectoire a été sectorisée en 2 sections qui vont d'abord de a à b puis de b à a.
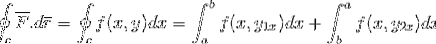
La définition du théorème fondamental du calcul est appliquée pour une intégrale définie.
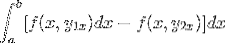
L'expression est réorganisée en une seule intégrale, le négatif devient un facteur commun et l'ordre des facteurs est inversé.
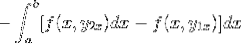
En observant cette expression en détail, il devient évident que lors de l'application des critères de fonction primitive, nous sommes en présence de l'intégrale de l'expression dérivée de f par rapport à y. Évalué en paramètres
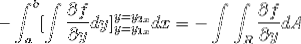
Il suffit maintenant de supposer que la fonction vectorielle F n'est définie que pour g (x, y)j. Lorsque, en fonctionnant d'une manière similaire au cas précédent, on obtient ce qui suit:
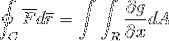
Pour finir, les 2 épreuves sont prises et jointes dans le cas où la fonction vectorielle prend des valeurs pour les deux versores. De cette manière, il est montré comment l'intégrale de ligne après avoir été définie et considérée comme une trajectoire unidimensionnelle, peut être pleinement développée pour le plan et l'espace.
F = f (x, y)je + g (x, y)j
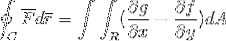
De cette façon, le théorème de Green est prouvé.
Applications
Les applications du théorème de Green sont larges dans les branches de la physique et des mathématiques. Celles-ci s'étendent à toute application ou utilisation pouvant être donnée à l'intégration de ligne.
Le travail mécanique effectué par une force F à travers un chemin C, peut être développé par une intégrale de ligne qui s'exprime comme une double intégrale d'une aire au moyen du théorème de Green.
Les moments d'inertie de nombreux corps soumis à des forces externes à différents points d'application répondent également à des intégrales de ligne qui peuvent être développées avec le théorème de Green..
Cela présente de multiples fonctionnalités dans les études de résistance des matériaux utilisés. Où les valeurs externes peuvent être quantifiées et prises en compte avant l'élaboration de divers éléments.
En général, le théorème de Green facilite la compréhension et la définition des zones où les fonctions vectorielles sont définies par rapport à une région selon une trajectoire.
Histoire
Il a été publié en 1828 dans l'ouvrage Analyse mathématique des théories de l'électricité et du magnétisme, écrit par le mathématicien britannique George Green. Dans celui-ci, des sections assez décisives dans l'application du calcul en physique sont explorées, telles que le concept de fonctions potentielles, les fonctions de Green et les applications de son théorème éponyme..
George Green a officialisé sa carrière d'étudiant à 40 ans, étant jusqu'à présent un mathématicien totalement autodidacte. Après des études à l'Université de Cambridge, il a poursuivi ses recherches, apportant des contributions sur l'acoustique, l'optique et l'hydrodynamique qui sont toujours d'actualité..
Relation avec d'autres théorèmes
Le théorème de Green est un cas particulier, et il découle de 2 autres théorèmes très importants dans le domaine du calcul. Ce sont le théorème de Kelvin-Stokes et le théorème de divergence ou Gauss Ostrogradski.
En partant de l'un ou l'autre des deux théorèmes, il est possible d'arriver au théorème de Green. Certaines définitions et propositions sont nécessaires pour développer de telles preuves..
Exercices
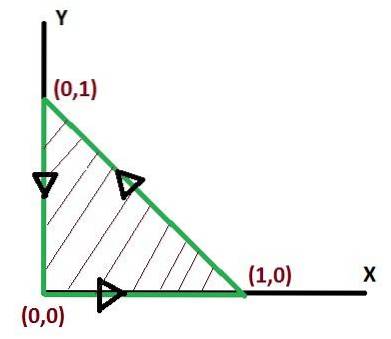
- L'exercice suivant montre comment transformer une intégrale de ligne en une double intégrale par rapport à une région R.
L'expression originale est la suivante:
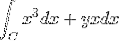
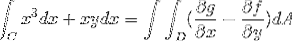
D'où sont tirées les fonctions correspondant à f et g
f (x, y) = x3 g (x, y) = yx
df / dy = 0 dg / dx = y
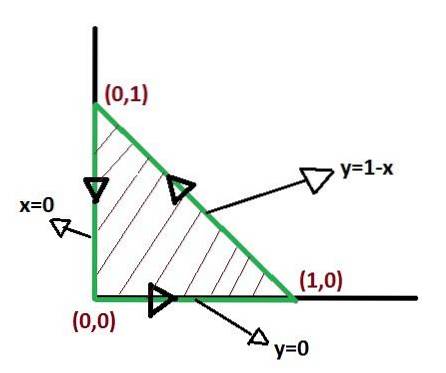
Il n'y a pas de manière unique de définir les limites de l'intégration lors de l'application du théorème de Green. Mais il existe des moyens où les intégrales après avoir été définies peuvent être plus simples. L'optimisation des limites d'intégration mérite donc une attention.
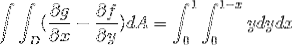
Où lors de la résolution des intégrales, nous obtenons:
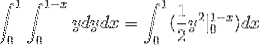
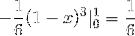
Cette valeur correspond en unités cubiques à la région sous la fonction vectorielle et sur la région triangulaire définie par C.
Pour le cas de l'intégrale de ligne sans effectuer la méthode de Green, il aurait fallu paramétrer les fonctions dans chaque section de la région. Autrement dit, effectuez 3 intégrales paramétrées pour la résolution. C'est une preuve suffisante de l'efficacité que Robert Green a apporté avec son théorème au calcul.
Les références
- Introduction à la mécanique du continuum. W Michael Lai, David H.Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23 juillet. 2009
- Calcul à variables multiples. James Stewart. Cengage Learning, 22 mars 2011
- Une histoire informelle du théorème de Green et des idées associées. James Joseph Cross. Département de mathématiques, Université de Melbourne, 1975
- Conduction thermique à l'aide des fonctions vertes. Kevin D. Cole, James V. Beck, A. Haji-Sheikh, Bahman Litkouhi. Taylor & Francis, 16 juil. 2010
- Application du théorème de Green à l'extrémisation des intégrales linéaires. Centre d'information technique de défense, 1961



Personne n'a encore commenté ce post.