le théorème des facteurs déclare qu'un polynôme P (x) est divisible par un binôme de la forme (x - a) si x = a est une racine de P (x), c'est-à-dire P (a) = 0. On dit qu'un polynôme est divisible entre un autre lorsque son résidu ou reste est nul.
Un polynôme est une expression de la forme:
P (x) = an Xn + àn-1 Xn-1 +… + A1 x + a0
Où:
-n est le degré du polynôme, où n est le plus grand entier auquel la variable indépendante x est élevée,
-Les valeurs àn, àn-1 ,… + A1 , à0 sont les coefficients du polynôme, qui sont généralement des nombres réels, mais qui pourraient aussi être des nombres complexes.
Un polynôme de degré n peut être décomposé comme le produit de n binômes de la forme:
(x - rje)
Où rje est la racine i-ème de P (x):
P (x) = an (x - r1) (x - rdeux)… (X - rn)
Puisque le nombre de racines d'un polynôme est égal à son degré.
Index des articles
Considérons par cas le polynôme:
P (x) = 3⋅xdeux - 7⋅x + 2
Vous voulez savoir si ce polynôme est divisible par le binôme (x - 2). Si le théorème des facteurs est utilisé, alors nous devons évaluer P (x = 2) pour savoir si la valeur 2 est une racine ou non. Nous procédons ensuite à l'évaluation de l'expression:
P (2) = 3⋅22 - 7⋅2 + 2 = 3⋅4 - 7⋅2 + 2 = 12 - 14 + 2 = 12 - 12 = 0.
Il s'avère que x = 2 est la racine de P (x), donc selon le théorème des facteurs, le binôme (x - 2) est effectivement un facteur de P (x).
Passons à la vérification directe en divisant. Le détail de la façon dont la division est effectuée est indiqué dans la figure suivante:
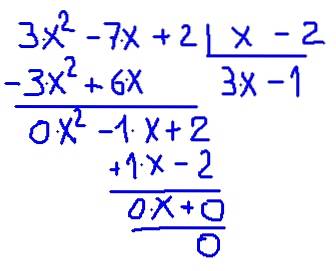
On vérifie que le quotient entre P (x) et (x-2) donne un polynôme de degré inférieur appelé quotient C (x) = 3⋅x - 1 avec reste 0.
Nous pouvons résumer le résultat comme suit:
(3⋅xdeux - 7⋅x + 2) ÷ (x -2) = (3⋅x - 1) + 0
L'expression précédente peut être écrite d'une autre manière, en se rappelant simplement que le dividende P (x) est égal au produit du diviseur (x -2) par le quotient (3⋅x - 1) plus le reste (zéro dans ce cas ):
(3⋅xdeux - 7⋅x + 2) = (x -2) (3⋅x - 1) + 0
De cette façon, il était possible de factoriser le polynôme P (x), c'est-à-dire d'écrire comme un produit de polynômes, le polynôme original:
(3⋅xdeux - 7⋅x + 2) = (x -2) (3⋅x - 1)
Soit le polynôme Q (x) = x3 - x + 2. On veut savoir s'il est divisible par le binôme (x + 1).
Le moyen le plus direct consiste simplement à appliquer le théorème des facteurs. Dans ce cas, il suffit de vérifier si x = -1 annule ou non le polynôme Q (x).
Nous procédons en remplaçant:
Q (-1) = (-1)3 - (-1) + 2 = -1 + 1 + 2 = 2
Le résultat est différent de zéro, donc le théorème du facteur nous assure que le polynôme Q (x) n'est pas divisible par (x + 1), puisque Q (-1) ≠ 0.
Nous allons maintenant procéder à la division de Q (x) par le binôme (x + 1) comme méthode de vérification de notre conclusion.
A cette occasion, la division sera effectuée selon la méthode de division synthétique, qui consiste à placer dans la première ligne ordonnée du degré le plus élevé au degré zéro tous les coefficients du polynôme, y compris les manquants, puisqu'ils ont un coefficient nul.
Ensuite, dans la première colonne, le terme indépendant du diviseur est placé mais avec le signe changé, dans notre cas, le diviseur est (x + 1). Son terme indépendant est 1, mais comme dans la première colonne, il est placé signe changé, c'est-à-dire -1.
La figure suivante illustre comment la division synthétique est effectuée:
Avec ce résultat on vérifie que (x + 1) n'est pas un facteur du polynôme Q (x) = x3 - x + 2 puisque le reste n'est pas nul.
Cette conclusion n'est pas surprenante, car elle avait déjà été prédite avec le théorème des facteurs. Notez également qu'en substituant x = -1 dans Q (x) ce qui est obtenu est précisément le reste ou le reste de la division des polynômes, puisque Q (-1) = reste = 2.
Bien entendu, la division fournit les informations supplémentaires du quotient C (x) = xdeux - X.
En se rappelant que le dividende Q (x) est égal au diviseur (x + 1) par le quotient C (x) plus le reste r = 2, nous avons le développement du polynôme Q (x) comme suit:
Q (x) = (x + 1) (xdeux - x) + 2 = x (x + 1) (x - 1) + 2
Il est à noter que cette expression n'est pas la factorisation dudit polynôme, puisqu'il y a un terme additionnel non nul, qui est précisément le reste de la valeur 2.
Trouvez les facteurs du polynôme
P (x) = x3 - 5 xdeux + 2 x + 8
Et écrivez aussi votre factorisation.
Le théorème des facteurs nous dit qu'il faut chercher les racines à pour ensuite trouver les facteurs (x - à), dans ce cas comme il s'agit d'un polynôme de degré trois, il doit y avoir trois racines.
Comme il s'agit d'un polynôme à coefficients entiers, les racines doivent être entre les diviseurs du terme indépendant, qui dans ce cas vaut 8. Ces diviseurs sont:
± 1, ± 2, ± 4, ± 8.
Nous commençons par explorer +1: P (+1) = 13 - 5⋅ 1deux + 2⋅1 + 8 = 1 - 5 + 2 + 8 = 6 qui est différent de 0, donc +1 n'est pas une racine.
Nous explorons -1:
P (-1) = (-1)3 - 5⋅ (-1)deux + 2⋅ (-1) + 8 = -1 - 5 - 2 + 8 = 0
À partir du résultat, on conclut que -1 est la racine de P (x) et (x - (-1)) = (x + 1) est un facteur du polynôme.
Deux autres facteurs restent à découvrir:
Nous prouvons ce qui suit qui vaut +2:
P (+2) = (+2)3 - 5⋅ (+2)deux + 2⋅ (+2) + 8 = 8 + (-20) + 4 + 8 = 0
Encore une fois, nous obtenons zéro. Donc, l'autre facteur est (x - 2).
Puisqu'il s'agit d'un polynôme de degré trois, il suffit de trouver un facteur. Maintenant, nous testons la valeur +4 pour savoir si elle annule le polynôme:
P (+4) = (+4)3 - 5⋅ (+4)deux + 2⋅ (+4) + 8 = 64 - 80 + 8 + 8 = 0.
Autrement dit, +4 est la racine de P (x) et donc le binôme (x - 4) est un autre de ses facteurs.
Plus besoin de chercher, car c'est un polynôme de degré 3 qui a au plus trois racines. Dans cet exercice, toutes les racines se sont révélées réelles et entières.
Par conséquent, le polynôme P (x) est factorisé comme ceci:
P (x) = x3 - 5 xdeux + 2 x + 8 = (x + 1) (x - 2) (x - 4).
Soit le polynôme p⋅x3 - x + 2p. Détermine la valeur de p pour que le polynôme soit divisible par (x + 2).
Nous utilisons le théorème du facteur, qui stipule que si x = -2 annule le polynôme alors (x - (-2)) est un facteur dudit polynôme.
Ensuite, nous substituons x à (-2) dans le polynôme d'origine, le simplifions et le définissons égal à zéro:
p⋅ (-2)3 - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0
Maintenant, la valeur de p est effacée afin que l'égalité à zéro soit satisfaite:
p = -2 / 10 = -⅕
Cela signifie que le polynôme:
-⅕⋅x3 - x - ⅖
Il est divisible par (x + 2), ou ce qui est équivalent: (x + 2) est l'un de ses facteurs.
Personne n'a encore commenté ce post.