Caractéristiques de tir parabolique, formules et équations, exemples

le tir parabolique Il consiste à lancer un objet ou un projectile à un certain angle et à le laisser se déplacer sous l'action de la gravité. Si la résistance de l'air n'est pas prise en compte, l'objet, quelle que soit sa nature, suivra un chemin d'arc de parabole.

C'est un mouvement quotidien, puisque parmi les sports les plus populaires sont ceux dans lesquels des balles ou des balles sont lancées, soit avec la main, avec le pied ou avec un instrument comme une raquette ou une batte par exemple..

Pour son étude, le tir parabolique se décompose en deux mouvements superposés: l'un horizontal sans accélération, et l'autre vertical avec une accélération constante vers le bas, qui est la pesanteur. Les deux mouvements ont une vitesse initiale.

Disons que le mouvement horizontal se déroule le long de l'axe x et le mouvement vertical le long de l'axe y. Chacun de ces mouvements est indépendant de l'autre.

La détermination de la position du projectile étant l'objectif principal, il est nécessaire de choisir un système de référence approprié. Les détails sont ci-dessous.

Index des articles

• 1 Formules et équations de tir parabolique
  • 1.1 - Trajectoire, hauteur maximale, temps maximal et portée horizontale
• 2 Exemples de tir parabolique
  • 2.1 Tir parabolique dans les activités humaines
  • 2.2 Le tir parabolique dans la nature
• 3 Exercice
• 4 Références

Formules et équations de tir parabolique

Supposons que l'objet soit projeté avec un angle α par rapport à la vitesse horizontale et initiale v_{ou alors} comme indiqué sur la figure ci-dessous à gauche. Le tir parabolique est un mouvement qui a lieu dans l'avion xy et dans ce cas, la vitesse initiale se décompose comme ceci:

v_bœuf = v_{ou alors} cos α

v_Hey = v_{ou alors} sin α

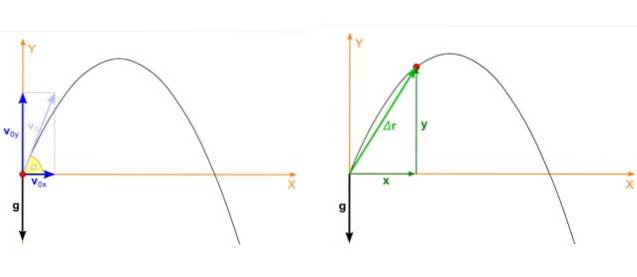
La position du projectile, qui est le point rouge de la figure 2, image de droite, a également deux composantes dépendant du temps, une en X et l'autre dans Oui. La position est un vecteur noté r et ses unités sont la longueur.

Sur la figure, la position initiale du projectile coïncide avec l'origine du système de coordonnées, donc x_{ou alors} = 0 et_{ou alors} = 0. Ce n'est pas toujours le cas, vous pouvez choisir l'origine n'importe où, mais ce choix simplifie grandement les calculs.

Quant aux deux mouvements en x et en y, ce sont:

-x (t): est un mouvement rectiligne uniforme.

-y (t): correspond à un mouvement rectiligne uniformément accéléré avec g = 9,8 m / s^deux et pointant verticalement vers le bas.

Sous forme mathématique:

x (t) = v_{ou alors} cos α.t

y (t) = v_{ou alors} .sin α.t - ½g.t^deux

Le vecteur de position est:

r (t) = [v_{ou alors} cos α.t]je + [v_{ou alors} .sin α.t - ½g.t^deux] j

Dans ces équations, le lecteur attentif remarquera que le signe moins est dû à la gravité pointant vers le sol, la direction choisie comme négative, tandis que vers le haut est considérée comme positive..

Puisque la vitesse est la première dérivée de la position, dérivez simplement r (t) en ce qui concerne le temps et obtenir:

v (t) = v_{ou alors} cos α je + (v_{ou alors} .sin α - gt) j

Enfin, l'accélération est exprimée de manière vectorielle par:

à (t) = -g j

- Trajectoire, hauteur maximale, durée maximale et portée horizontale

Trajectoire

Pour trouver l'équation explicite du chemin, qui est la courbe y (x), nous devons éliminer le paramètre de temps, en résolvant l'équation pour x (t) et en le substituant en y (t). La simplification est un peu laborieuse, mais finalement vous obtenez:

Hauteur maximale

La hauteur maximale se produit lorsque v_Oui = 0. Sachant qu'il existe la relation suivante entre la position et le carré de la vitesse:

v_Oui^deux = v_Hey ^deux- 2gy

En faisant v_Oui = 0 juste en atteignant la hauteur maximale:

0 = v_Hey ^deux- 2g. Et_max → et_max = v_Hey ^deux/ 2 g

Avec:

v_Hey = v_{ou alors} senα

Temps maximum

Le temps maximum est le temps qu'il faut à l'objet pour atteindre et_max. Pour le calculer, on utilise:

v_Oui = v_{ou alors} .sin α - gt

Sachant que v_Oui devient 0 quand t = t_max, résultat:

v_{ou alors} .sin α - g.t_max = 0

t_max = v_Hey / g

Portée horizontale maximale et temps de vol

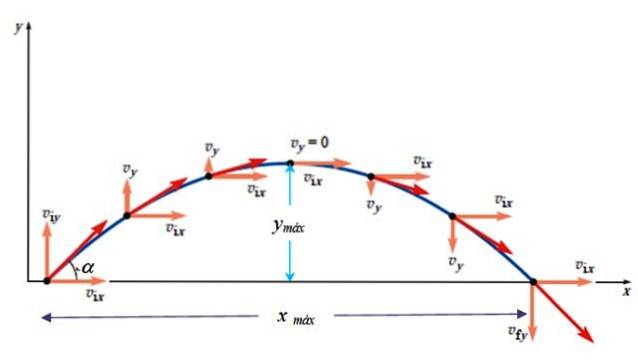
La portée est très importante, car elle signale où l'objet tombera. De cette façon, nous saurons s'il atteint ou non la cible. Pour le trouver, nous avons besoin du temps de vol, du temps total ou de t_v.

À partir de l'illustration ci-dessus, il est facile de conclure que t_v = 2.t_max. Mais attention, cela n'est vrai que si le lancement est de niveau, c'est-à-dire que la hauteur du point de départ est la même que la hauteur de l'arrivée. Sinon, le temps est trouvé en résolvant l'équation quadratique qui résulte de la substitution de la position finale Oui_final:

Oui_final = v_{ou alors} .sin α.t_v - ½g.t_v^deux

Dans tous les cas, la portée horizontale maximale est:

X_max = v_bœuf. t_v

Exemples de tir parabolique

Le tir parabolique fait partie du mouvement des personnes et des animaux. Aussi de presque tous les sports et jeux où la gravité intervient. Par exemple:

Tir parabolique dans les activités humaines

-La pierre lancée par une catapulte.

-Le coup de pied de but du gardien.

-La balle lancée par le lanceur.

-La flèche qui sort de l'arc.

-Toutes sortes de sauts

-Jeter une pierre avec une écharpe.

-Toute arme lancée.

Le tir parabolique dans la nature

-L'eau qui jaillit de jets naturels ou artificiels comme ceux d'une fontaine.

-Pierres et lave jaillissant d'un volcan.

-Une balle qui rebondit sur le trottoir ou une pierre qui rebondit sur l'eau.

-Toutes sortes d'animaux sauteurs: kangourous, dauphins, gazelles, chats, grenouilles, lapins ou insectes, pour n'en nommer que quelques-uns.

Exercer

Une sauterelle saute à un angle de 55 ° avec l'horizontale et atterrit à 0,80 mètre devant. Trouve:

a) La hauteur maximale atteinte.

b) S'il sautait avec la même vitesse initiale, mais formant un angle de 45 °, irait-il plus haut??

c) Que dire de la portée horizontale maximale pour cet angle?

Solution pour

Lorsque les données fournies par le problème ne contiennent pas la vitesse initiale v_{ou alors} les calculs sont un peu plus laborieux, mais à partir des équations connues, une nouvelle expression peut être dérivée. À partir de:

X_max = v_bœuf . t_vol = v_{ou alors}.cos α. t_v

Lorsqu'il atterrit plus tard, la hauteur revient à 0, donc:

v_{ou alors} .sin α.t_v - ½g.t_v^deux= 0

Quoi t_v est un facteur commun, il est simplifié:

v_{ou alors} .sin α - ½g.t_v= 0

Nous pouvons effacer t_v à partir de la première équation:

t_v = x_max / v_{ou alors}.cos α

Et remplacez dans le second:

v_{ou alors} .sin α - (½g.x_max / v_{ou alors}.cos α) = 0

En multipliant tous les termes par v_{ou alors}.cos αl'expression n'est pas modifiée et le dénominateur disparaît:

(v_{ou alors} .sin α.) (v_{ou alors}.cos α) - ½g.x_max = 0

v_{ou alors}^deux sin α. cos α = ½g.x_max

Il peut déjà être effacé v_{ou alors} ou remplacez également l'identité suivante:

sin 2α = 2 sin α. cos α → v_{ou alors}^deux sin 2α = g.x_max

Se calcule v_{ou alors}^deux:

v_{ou alors}^deux = g.X_max / sin 2α = (9,8 x 0,8 / sin 110) m^deux/ s^deux = 8,34 m^deux/ s^deux

Et enfin la hauteur maximale:

Oui_max= v_Hey ^deux/ 2g = (8,34 x sin^deux 55) / (2 x 9,8) m = 0,286 m = 28,6 cm

Solution b

Le homard parvient à maintenir la même vitesse horizontale, mais en diminuant l'angle:

Oui_max= v_Hey ^deux/ 2g = (8,34 x péché^deux 45) / (2 x 9,8) m = 0,213 m = 21,3 cm

Atteint une hauteur inférieure.

Solution c

La portée horizontale maximale est:

X_max = v_{ou alors}^deux sen 2ème / g

En faisant varier l'angle, la portée horizontale change également:

X_max = 8,34 sen 90 / 9,8  m = 0,851 m = 85,1 cm

Le saut est plus long maintenant. Le lecteur peut vérifier qu'il est maximal pour l'angle de 45 ° car:

sin 2α = sin 90 = 1.

Les références

1. Figueroa, D. 2005. Série: Physique pour les sciences et l'ingénierie. Volume 1. Cinématique. Edité par Douglas Figueroa (USB).
2. Giambattista, A. 2010. Physique. Deuxième édition. Mcgraw Hill.
3. Giancoli, D. 2006. Physique: principes avec applications. 6e. Salle des Prentices Ed.
4. Resnick, R. 1999. Physique. Vol. 1. 3e éd. En espagnol. Compañía Editorial Continental S.A. par C.V.
5. Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 1.