
Travail de formule, unités, exemples, exercices

le travail En physique c'est le transfert d'énergie effectué par une force lorsque l'objet sur lequel elle agit se déplace. Mathématiquement, il prend la forme du produit scalaire entre les vecteurs de force F et déplacement s.
Et comme le produit scalaire entre deux vecteurs perpendiculaires est nul, il arrive que les forces qui forment 90º avec le déplacement ne fonctionnent pas, selon la définition, puisque:
W = F ● s = F⋅ s⋅ cos θ
Où W désigne le travail, du mot anglais travail.
L'avantage de définir le travail est qu'il s'agit d'un scalaire, c'est-à-dire qu'il n'a ni direction ni sens, seulement le module et l'unité respective. Cela facilite les calculs impliquant des changements d'énergie provoqués par l'action des forces..
La gravité et le frottement cinétique sont des exemples de forces qui agissent souvent sur des objets en mouvement. Une autre force courante est la force normale exercée par une surface, mais contrairement à celles-ci, elle ne travaille jamais sur les objets, car elle est perpendiculaire au déplacement..
Lorsqu'un corps tombe librement, la gravité effectue un travail positif sur le mobile, l'amenant à augmenter sa vitesse lors de sa chute. Par contre, le frottement cinétique a un effet complètement opposé, car comme il s'oppose toujours au mouvement, il effectue un travail négatif qui ne le favorise pas..
Index des articles
- 1 Formules et cas particuliers
- 1.1 Travail effectué par des forces variables
- 2 unités de travail
- 2.1 Unités dans le système britannique
- 2.2 Autres unités de travail
- 3 Exemples de travaux
- 3.1 Montée et descente d'objets
- 3.2 Charges ponctuelles dans les champs électriques
- 3.3 Friction entre les surfaces
- 3.4 Pousser et tirer
- 3.5 Force dans une poulie
- 3.6 Forces ou supports normaux
- 3.7 Force magnétique
- 3.8 Objets attachés à une corde
- 3.9 Satellites en orbite
- 3.10 Système masse-ressort
- 4 Exercice résolu
- 5 Références
Formules et cas particuliers
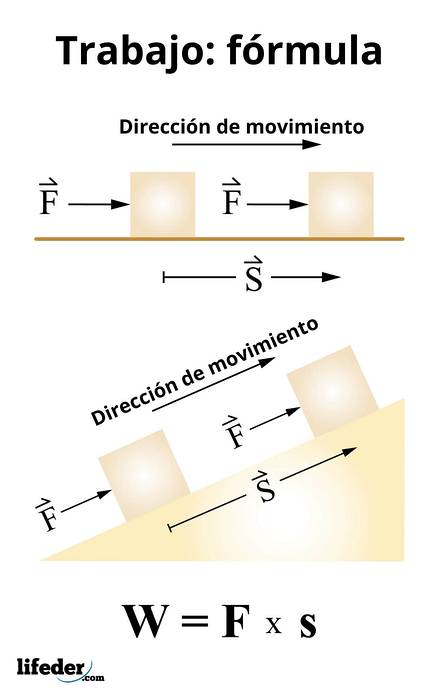
Le travail est calculé par:
W = F ● s
Cette expression est valable pour des forces constantes et selon la définition d'un produit scalaire, elle équivaut à:
W = F. s. cos θ
Où θ est l'angle entre la force et le déplacement. Il s'ensuit donc que seules les forces qui ont une composante dans la direction du déplacement peuvent travailler sur un corps.
Et il devient aussi clair que s'il n'y a pas de mouvement, il n'y a pas non plus de travail.
Quant au signe, le travail peut être positif, négatif ou nul. Dans le cas où la force a une composante parallèle au mouvement, le signe du travail dépend de la valeur de cos θ.
Certains cas particuliers méritent d'être considérés:
- Lorsque la force est parallèle au déplacement, l'angle entre F Oui s est 0º, donc le travail effectué par la force est positif et sa valeur est maximale:
W = F⋅s cos 0º = F⋅s
- Si la force s'oppose au déplacement, alors l'angle entre F Oui s est de 180 °, le travail effectué par F est négatif et il est minimal:
W = F⋅s cos 180º = -F⋅s
- Enfin, il y a le cas évoqué précédemment: si l'angle formé par F Oui s est 90º, puisque cos 90º = 0, le travail est nul:
W = F⋅s cos 90º = 0
Travail effectué par des forces variables
Parfois, la force appliquée n'est pas constante; dans ce cas, il faut recourir au calcul pour trouver le travail effectué. Tout d'abord, un différentiel de travail dW est déterminé, effectué sur un déplacement infinitésimal ds:
dW = F⋅rés
Pour trouver la valeur du travail total effectué par cette force lorsque l'objet passe du point A au point B, il faut intégrer les deux côtés, comme ceci:
Unités de travail
L'unité de travail dans le système international est le joule, en abrégé J. L'unité tire son nom du physicien anglais James Prescott Joule, pionnier dans l'étude de la thermodynamique..
D'après l'équation de travail, le joule est défini comme 1 newton par mètre:
1 J = 1 N⋅m
Unités dans le système britannique
Le travail correspond comme une unité livre-force x pied, parfois appeler pied livre-force. C'est aussi une unité d'énergie, mais il faut se rappeler que le travail effectué sur un corps modifie son état énergétique et que donc travail et énergie sont équivalents. Pas étonnant qu'ils aient les mêmes lecteurs.
L'équivalence entre le pied livre-force et le joule est la suivante:
1 pied-livre-force = 1.35582 J
Une unité bien connue pour le travail et l'énergie, en particulier pour le domaine de la réfrigération et de la climatisation est le BTU ou Unité thermique britannique.
1 BTU équivaut à 1055 J et à 778169 pieds-livre-force.
Autres unités de travail
Il existe d'autres unités de travail qui sont utilisées dans des domaines spécifiques de la physique et de l'ingénierie. Parmi eux, nous avons:
Erg
Désigné comme erg, est l'unité de travail dans le système cégésimal et est égal à 1 dyna⋅cm ou 1 x 10-7 J.
Électron-volt
EV abrégé, il est couramment utilisé en physique des particules et est défini comme l'énergie qu'un électron acquiert lorsqu'il se déplace à travers une différence de potentiel de 1 V.
Kilowattheure (kWh)
Il apparaît fréquemment sur les factures de services publics. C'est le travail effectué pendant 1 heure par une source dont la puissance est de 1 kW, soit 3,6 x 106 J.
Calorie
Il est généralement lié à l'énergie des aliments, bien qu'en fait, dans ce contexte, il soit fait référence à un kilocalorie, c'est-à-dire 1000 calories. En fait, il y a plusieurs unités qui reçoivent ce nom, donc le contexte doit être très bien spécifié.
L'équivalence entre le joule et 1 calorie thermochimique c'est:
1 calorie = 4,1840 J
Exemples de travail
Montée et descente d'objets
Lorsque les corps descendent, soit verticalement, soit sur une rampe, le poids fait un travail positif, favorisant le mouvement. Au lieu de cela, chaque fois qu'un objet monte, la gravité fait un travail négatif.
Charges ponctuelles dans les champs électriques
Un champ électrique uniforme fonctionne sur une charge ponctuelle se déplaçant à l'intérieur. Selon le terrain et le signe de la charge, ce travail peut être négatif ou positif.
Friction entre les surfaces
Le frottement cinétique entre les surfaces fait toujours un travail négatif sur l'objet en mouvement.
Pousser et tirer

Pousser est une force qui éloigne un objet de quelque chose. Tirer est une force qui fait qu'un objet se rapproche.
Force dans une poulie
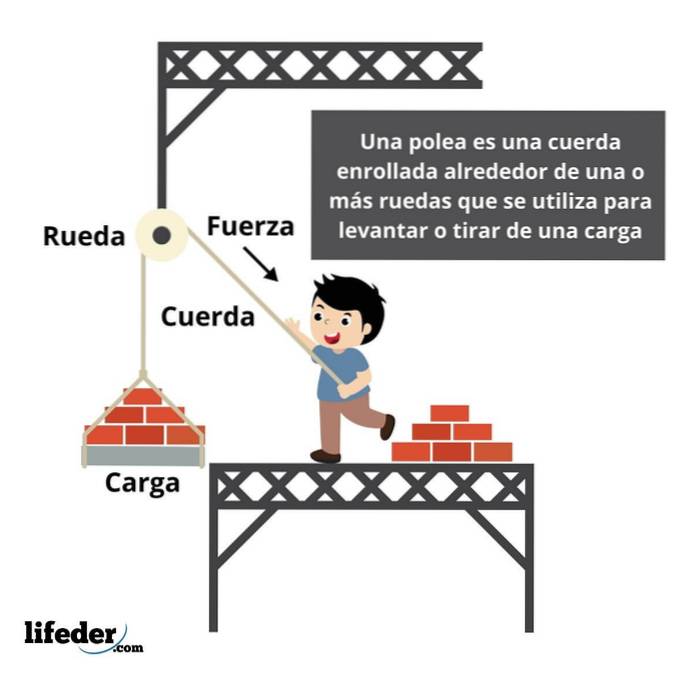
Une poulie est un système utilisé pour transmettre une force à l'une de ses extrémités. Dans une poulie simple, afin de soulever la charge, une force égale à la résistance exercée par l'objet doit être appliquée.
Forces ou supports normaux
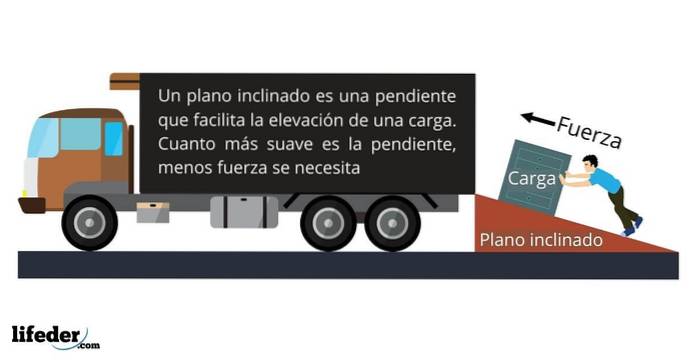
La normale, comme indiqué ci-dessus, ne fonctionne pas lorsqu'un objet posé sur une surface se déplace dessus, même si la surface n'est pas plane ou si elle est inclinée..
Force magnétique
Une autre force qui ne fait aucun travail est la force magnétique qui exerce un champ uniforme sur la particule chargée qui lui est perpendiculaire. Le mouvement de la particule s'avère être un mouvement circulaire uniforme, avec la force dans la direction radiale. Le déplacement étant perpendiculaire à la force, il ne fonctionne pas sur la charge..
Objets attachés à une corde
Une corde ne fonctionne pas non plus sur un pendule suspendu, car sa tension est toujours perpendiculaire au déplacement de la masse..
Satellites en orbite
La gravité ne fonctionne pas non plus sur un satellite en orbite circulaire, pour la même raison que les cas précédents: elle est perpendiculaire au déplacement..
Système masse-ressort
Dans un système masse-ressort, la force F que le ressort exerce sur la masse a une grandeur F = kx, où k est la constante du ressort et X sa compression ou son allongement. C'est une force variable, donc le travail qu'elle fait dépend de combien le ressort s'étire ou rétrécit.
Exercice résolu
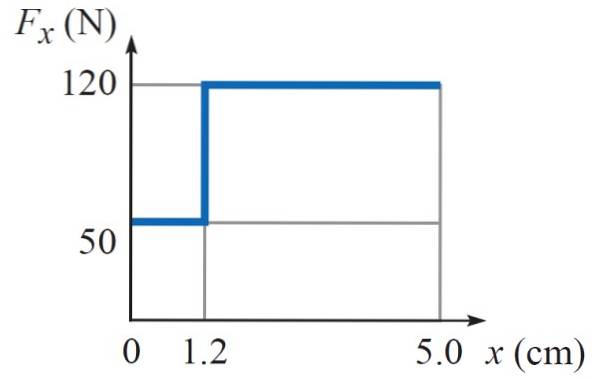
Le graphique suivant montre le travail effectué par une force variable FX qui dépend de la position X. C'est la force exercée par un marteau sur un clou. La première partie est la force utilisée pour clouer sur la section la plus molle du mur et la seconde pour finir d'enfoncer le clou.
Combien de travail le marteau doit-il faire pour que le clou s'enfonce un total de 5 cm dans le mur?
Solution
La force exercée par le marteau est variable, car il faut moins d'intensité (50 N) pour enfoncer le clou de 1,2 cm dans la partie molle du mur, tandis que dans la partie la plus dure, il faut 120 N pour faire couler le clou jusqu'à 5 cm de profondeur, comme indiqué dans le tableau.
Dans ce cas, l'œuvre est l'intégrale:

Où A = 0 cm et B = 5 cm. Puisque l'intégrale est l'aire sous le graphe Fx vs x, il suffit de trouver cette aire, qui correspond à deux rectangles, le premier de hauteur 50 N et largeur 1,2 cm, et le second de hauteur 120 N et largeur (5 cm - 1,2 cm) = 3,8 cm.
Les deux sont calculés et ajoutés pour donner le travail total:
L = 50 N x 1,2 cm + 120 N x 3,8 cm = 516 N.cm = 516 N x 0,01 m = 5,16 J.
Les références
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 2. Dynamique. Edité par Douglas Figueroa (USB).
- Giambattista, A. 2010. Physique. 2ème. Ed. McGraw Hill.
- Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 1. Pearson.
- Serway, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7e. Éd. Cengage Learning.
- Zapata, F. Travaux mécaniques. Récupéré de: francesphysics.blogspot.com.



Personne n'a encore commenté ce post.