
Caractéristiques des vecteurs simultanés, exemples et exercices
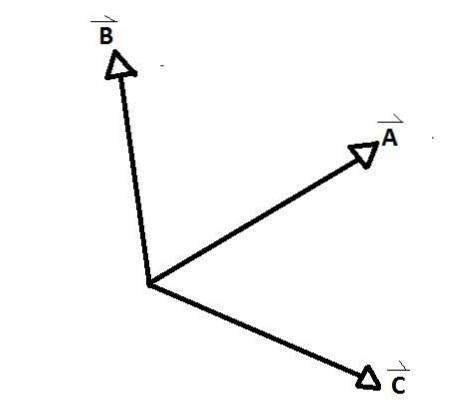
Les vecteurs simultanés sont les groupes de vecteurs dont les axes coïncident en un point, formant entre chaque paire d'entre eux un angle interne et un angle externe. Un exemple clair est vu dans la figure ci-dessous, où A, B et C sont des vecteurs simultanés les uns avec les autres.
D et E contrairement aux autres ne le sont pas. Il y a des angles formés entre les vecteurs concurrents AB, AC et CB. Ils sont appelés angles de relation entre les vecteurs.
Index des articles
- 1 Fonctionnalités
- 2 types de vecteurs
- 3 Notation vectorielle
- 3.1 cartésien
- 3.2 Polaire
- 3.3 Analytique
- 3.4 Sphérique
- 4 Opérations avec des vecteurs simultanés
- 4.1 Somme (A + B)
- 4.2 Différence (A - B)
- 4.3 Produit scalaire (A. B)
- 4.4 Produit vectoriel (A x B)
- 5 Exemples: exercices résolus
- 5.1 Exercice 1
- 5.2 Exercice 2
- 6 Exercices proposés
- 7 Références
Caractéristiques
-Ils ont un point commun, qui coïncide avec leur origine: toutes les grandeurs des vecteurs concurrents partent d'un point commun vers leurs extrêmes respectifs..
-L'origine est considérée comme le point d'action du vecteur: il faut établir un point d'action qui sera directement affecté par chacun des vecteurs concurrents.
-Son domaine dans le plan et l'espace est Rdeux et R3 respectivement: les vecteurs concurrents sont libres de couvrir tout l'espace géométrique.
-Il permet différentes notations dans le même groupe de vecteurs. Selon les branches d'étude, différentes notations sont présentes dans les opérations avec des vecteurs.
Types de vecteurs
La branche des vecteurs a plusieurs subdivisions, dont certaines peuvent être nommées: parallèle, perpendiculaire, coplanaire, correspondante, opposée et unitaire. Les vecteurs simultanés sont répertoriés ici et, comme tous ceux cités ci-dessus, ils ont de nombreuses applications dans différentes sciences..
Ils sont très courants dans l'étude des vecteurs, car ils représentent une généralisation utile dans les opérations avec eux. Tant dans le plan que dans l'espace, les vecteurs concurrents sont couramment utilisés pour représenter différents éléments et étudier leur influence sur un système particulier..
Notation vectorielle
Il existe plusieurs façons de représenter un élément vectoriel. Les principaux et les plus connus sont:
cartésien
Proposé par cette même approche mathématique, il désigne les vecteurs par un triple correspondant aux grandeurs de chaque axe (x, y, z)
A: (1, 1, -1) Espace A: (1, 1) Avion
Polaire
Ils ne servent qu'à désigner les vecteurs dans le plan, bien que dans le calcul intégral, on leur attribue la composante de profondeur. Il est composé d'une magnitude linéaire r et un angle par rapport à l'axe polaire Ɵ.
A: (3, 450 ) Plan A: (2, 450 , 3) Espace
Analytique
Ils définissent les magnitudes du vecteur en utilisant les versores. Les versores (i + j + k) représentent les vecteurs unitaires correspondant aux axes X, Y Oui
A: 3i + 2j - 3k
Sphérique
Ils sont similaires à la notation polaire, mais avec l'ajout d'un deuxième angle qui balaie le plan xy symbolisé par δ.
A: (4, 60ou alors , π / 4)
Opérations vectorielles simultanées
Les vecteurs simultanés sont principalement utilisés pour définir des opérations entre vecteurs, car il est plus facile de comparer les éléments des vecteurs lorsqu'ils sont présentés simultanément..
Somme (A + B)
La somme des vecteurs concurrents vise à trouver le vecteur résultant Vr. Ce qui, selon la filière d'étude, correspond à une action finale
Par exemple: 3 chaînes A, B, C sont liées à une boîte, chaque extrémité de la chaîne est tenue par un sujet. Chacun des 3 sujets doit tirer la corde dans une direction différente des 2 autres.
A: (ax, ay, az) B: (bx, by, bz) C: (cx, cy, cz)
A + B + C = (ax + bx + cx; ay + par + cy; az + bz + cz) = Vr
La boîte ne pourra se déplacer que dans une seule direction, donc Vr indiquera la direction et la direction du mouvement de la boîte.
Différence (A - B)
Il existe de nombreux critères concernant la différence entre les vecteurs, de nombreux auteurs choisissent de l'exclure et déclarent que seule la somme entre les vecteurs est stipulée, où la différence concerne la somme du vecteur opposé. La vérité est que algébriquement les vecteurs peuvent être soustraits.
A: (ax, ay, az) B: (bx, by, bz)
A - B = A + (-B) = (ax-bx; ay-by; az-bz) = [ax + (-bx); ay + (-by); az + (-bz)]
Produit scalaire (A. B)
Aussi connu sous le nom de produit scalaire, il génère une valeur scalaire qui peut être liée à différentes grandeurs en fonction de la branche d'étude..
Pour la géométrie, indique l'aire du parallélogramme formée par la paire de vecteurs simultanés par la méthode du parallélogramme. Pour la physique mécanique définir le travail effectué par une force F lors du déplacement d'un corps à distance Δr.
ѡ = F . Δr
Comme son nom l'indique, il génère une valeur scalaire et se définit comme suit:
Soit les vecteurs A et B
A: (ax, ay, az) B: (bx, by, bz)
-Forme analytique:
(A. B) = | A |. | B | .Cos θ
Où θ est l'angle interne entre les deux vecteurs
-Forme algébrique:
(A. B) = (ax.bx + ay.by + az.bz)
Produit croisé (A x B)
Le produit croisé ou produit ponctuel entre deux vecteurs, définit un troisième vecteur C qui a la qualité d'être perpendiculaire à B Oui C. En physique, définir le vecteur couple τ élément de base de la dynamique de rotation.
-Forme analytique:
| A x B | = | A |. | B | .Sen θ
-Forme algébrique:
(A x B) = = (Ax. By - ay. Bx) - (ax. Bz - az. Bx) j + (ax. par - ay. bx) k
-Mouvement relatif: rUN B
La base de la relativité est le mouvement relatif et les vecteurs concurrents sont la base du mouvement relatif. Les positions, vitesses et accélérations relatives peuvent être déduites en appliquant l'ordre d'idées suivant.
r UN B = rÀ - rB ; Position relative de A par rapport à B
v UN B = vÀ - vB ; Vitesse relative de A par rapport à B
à UN B = aÀ - àB ; Accélération relative de A par rapport à B
Exemples: exercices résolus
Exercice 1
Soit A, B et C des vecteurs concurrents.
A = (-1, 3, 5) B = (3, 5, -2) C = (-4, -2, 1)
-Définir le vecteur résultant Vr = 2A - 3B + C
2A = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)
-3B = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)
Vr = 2A + (-3B) + C = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)
Vr = ([-2 + (- 9) + (- 4)]; [6 + (- 15) + (- 2)]; (10 + 6 + 1))
Vr = (-15, -11, 17)
-Définir le produit scalaire (A. C)
(A. C) = (-1, 3, 5). (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4-6 + 5
(A. C) = 3
-Calculez l'angle entre A et C
(A. C) = | A |. | C |. Cos θ Où θ est l'angle le plus court entre les vecteurs
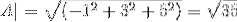
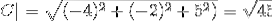
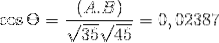
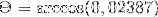
θ = 88,630
-Trouver un vecteur perpendiculaire à A et B
Pour cela, il est nécessaire de définir le produit vectoriel entre (-1, 3, 5) et (3, 5, -2). Comme expliqué précédemment, une matrice 3 x 3 est construite où la première ligne est composée des vecteurs à trois unités (i, j, k). Puis les 2ème et 3ème rangées sont constituées des vecteurs à opérer, en respectant l'ordre opérationnel.
(A x B) = = [(-1). 5 - (3. 3)] je - [ (-1) . (-2) - (5. 3)] j + [ (-1) . 5 - (3. 3)] k
(A x B) = (-5 - 9) je - (2 - 15) j + (-5 - 9) k
(A x B) = -14 I + 13 j - 14 k
Exercice 2
Soit Và et Vb les vecteurs de vitesse de A et B respectivement. Calculez la vitesse de B vue de A.
Và = (3, -1, 5) Vb = (2, 5, -3)
Dans ce cas, la vitesse relative de B par rapport à A est demandée VB / A
VB / A = VB - VÀ
VB / A = (2, 5, -3) - (3, -1, 5) = (-1, 6, -8)
C'est le vecteur vitesse de B vu de A. Où un nouveau vecteur de vitesse de B est décrit en prenant référence d'un observateur positionné en A et se déplaçant avec la vitesse de A.
Exercices proposés
1-Construire 3 vecteurs A, B et C qui sont simultanés et relier 3 opérations entre eux à travers un exercice pratique.
2-Soit les vecteurs A: (-2, 4, -11), B: (1, -6, 9) et C: (-2, -1, 10). Trouver des vecteurs perpendiculaires à: A et B, C et B, La somme A + B + C.
4-Déterminer 3 vecteurs perpendiculaires entre eux, sans tenir compte des axes de coordonnées.
5-Définir le travail effectué par une force qui soulève un bloc de masse de 5 kg, depuis le fond d'un puits de 20m de profondeur.
6-Montrer algébriquement que la soustraction des vecteurs est égale à la somme du vecteur opposé. Justifiez vos postulats.
7-Désignez un vecteur dans toutes les notations développées dans cet article. (Cartésien, polaire, analytique et sphérique).
8-Les forces magnétiques exercées sur un aimant qui repose sur une table, sont données par les vecteurs suivants; V: (5, 3, -2), T: (4, 7, 9), H: (-3, 5, -4). Déterminez dans quelle direction l'aimant se déplacera si toutes les forces magnétiques agissent en même temps.
Les références
- Géométrie euclidienne et transformations. Clayton W. Dodge. Courier Corporation, 1 janvier 2004
- Comment résoudre des problèmes de mathématiques appliquées L. Moiseiwitsch. Courier Corporation, 10 avril 2013
- Concepts de base de la géométrie. Walter Prenowitz, Meyer Jordan. Rowman & Littlefield, 4 octobre 2012
- Vecteurs. Rocío Navarro Lacoba, 7 juin. 2014
- Algèbre linéaire. Bernard Kolman, David R. Hill. Pearson Education, 2006



Personne n'a encore commenté ce post.