
Vecteurs teamlenses définition, notation, exercices
Deux ou plus les vecteurs sont la lentille de l & # 39; équipe s'ils ont le même module, la même direction et le même sens, même si leur point d'origine est différent. Rappelez-vous que les caractéristiques d'un vecteur sont précisément: l'origine, le module, la direction et le sens.
Les vecteurs sont représentés par un segment orienté ou une flèche. La figure 1 montre la représentation de plusieurs vecteurs dans le plan, dont certains sont en équipe selon la définition donnée initialement..
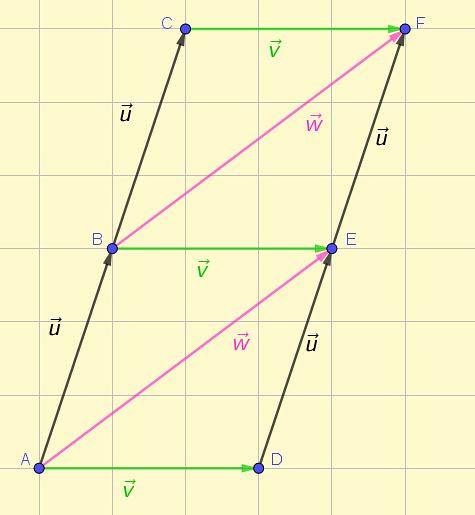
Au premier coup d'œil, il est possible de voir que les trois vecteurs verts ont la même taille, la même direction et le même sens. On peut dire la même chose des deux vecteurs roses et des quatre vecteurs noirs.
De nombreuses grandeurs de la nature ont un comportement de type vectoriel, comme c'est le cas de la vitesse, de l'accélération et de la force, pour n'en nommer que quelques-unes. D'où l'importance de bien les caractériser.
Index des articles
- 1 Notation pour les vecteurs et l'équipement
- 1.1 Vecteurs libres, glissants et opposés
- 2 exercices
- 2.1 -Exercice 1
- 2.2 -Exercice 2
- 2.3 -Exercice 3
- 3 Références
Notation des vecteurs et des équipements
Pour distinguer les quantités vectorielles des quantités scalaires, le caractère gras ou une flèche au-dessus de la lettre est souvent utilisé. Lorsque vous travaillez avec des vecteurs à la main, sur le cahier, il est nécessaire de les distinguer avec la flèche et lors de l'utilisation d'un support imprimé, des caractères gras sont utilisés.
Les vecteurs peuvent être désignés en indiquant leur point de départ ou d'origine et leur point d'arrivée. Par exemple UN B, avant JC, DE Oui EF de la figure 1 sont des vecteurs, à la place UN B, avant JC, DE Oui EF sont des quantités scalaires ou des nombres qui indiquent la grandeur, le module ou la taille de leurs vecteurs respectifs.
Pour indiquer que deux vecteurs sont orientés équipe, le symbole "∼ ". Avec cette notation, dans la figure, nous pouvons souligner les vecteurs suivants qui sont orientés équipe les uns par rapport aux autres:
AB∼BC∼DE∼EF
Ils ont tous la même ampleur, la même direction et la même signification. Par conséquent, ils sont conformes aux réglementations indiquées ci-dessus..
Vecteurs libres, glissants et opposés
L'un des vecteurs de la figure (par exemple UN B) est représentatif de l'ensemble de tous les vecteurs fixes équipement-lentille. Cet ensemble infini définit la classe des vecteurs libres ou alors.
ou alors = AB, BC, DE, EF, ...
Une notation alternative est la suivante:
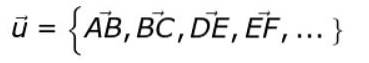
Si le gras ou la petite flèche n'est pas placé au-dessus de la lettre ou alors, est que l'on veut se référer au module vectoriel ou alors.
Les vecteurs libres ne sont appliqués à aucun point particulier.
Pour leur part vecteurs glissants Ce sont des vecteurs de longueur d'équipe vers un vecteur donné, mais leur point d'application doit être contenu dans la ligne d'action du vecteur donné.
Et les vecteurs opposés Ce sont des vecteurs qui ont la même ampleur et la même direction, mais des sens opposés, bien que dans les textes anglais, ils soient appelés de directions opposées puisque la direction indique également le sens. Les vecteurs opposés ne font pas équipe.
Exercices
-Exercice 1
Quels autres vecteurs parmi ceux illustrés dans la figure 1 sont liés les uns aux autres??
Solution
En dehors de ceux déjà indiqués dans la section précédente, on observe à partir de la figure 1 que UN D, ÊTRE Oui CE Ce sont également des vecteurs d'équipe:
AD ∼ BE ∼ CE
Chacun d'eux est représentatif de la classe des vecteurs libres v.
Les vecteurs AE Oui BF :
AE ∼ BF
Qui sont les représentants de la classe w.
-Exercice 2
Les points A, B et C sont sur le plan cartésien XY et leurs coordonnées sont:
A = (- 4,1), B = (- 1,4) et C = (- 4, -3)
Trouvez les coordonnées d'un quatrième point D telles que les vecteurs UN B Oui CD être orienté équipe.
Solution
Pour que CD être orienté équipe UN B doit avoir le même module et la même adresse que UN B .
Le module UN B au carré est:
|UN B| ^ 2 = (-1 - (-4)) ^ 2 + (4-1) ^ 2 = 9 + 9 = 18
Les coordonnées de D sont inconnues, nous pouvons donc dire: D = (x, y)
Puis: |CD| ^ 2 = (x - (- 4)) ^ 2 + (y - (-3)) ^ 2
As |UN B| = |CD| est l'une des conditions pour UN B Oui CD être orienté équipe, vous avez:
(x + 4) ^ 2 + (y + 3) ^ 2 = 18
Puisque nous avons deux inconnues, une autre équation est nécessaire, qui peut être obtenue à partir de la condition que UN B Oui CD sont parallèles et dans le même sens.
Pente du vecteur AB
La pente vectorielle UN B indique votre adresse:
Pente AB = (4-1) / (- 1 - (-4)) = 3/3 = 1
Indiquant que le vecteur UN B 45º avec l'axe X.
Pente du CD vectoriel
La pente de CD est calculé de la même manière:
Pente CD = (y - (-3)) / (x - (- 4)) = (y + 3) / (x + 4)
En assimilant ce résultat à la pente de UN B nous avons l'équation suivante:
y + 3 = x + 4
Ce qui signifie que y = x + 1.
Si ce résultat est substitué dans l'équation pour l'égalité des modules, on a:
(x + 4) ^ 2 + (x + 1 + 3) ^ 2 = 18
Simplifier cela reste:
2 (x + 4) ^ 2 = 18,
Ce qui équivaut à:
(x + 4) ^ 2 = 9
Autrement dit, x + 4 = 3, ce qui implique que x = -1. Donc les coordonnées de D sont (-1, 0).
Chèque
Les composants du vecteur UN B sont (-1 - (- 4), 4-1) = (3, 3)
et le vecteur CD sont (-1 - (- 4)); 0 - (- 3)) = (3, 3)
Ce qui signifie que les vecteurs sont orientés équipe. Si deux vecteurs ont les mêmes composantes cartésiennes, ils ont le même module et la même direction, donc ils sont en équipe..
-Exercice 3
Le vecteur libre ou alors a la magnitude 5 et la direction 143.1301º.
Trouvez leurs composantes cartésiennes et déterminez les coordonnées des points B et C sachant que les vecteurs fixes AB et CD sont orientés équipe vers u. Les coordonnées de A sont (0, 0) et les coordonnées du point C sont (-3,2).
Solution
La situation posée par l'exercice peut être représentée par la figure suivante:
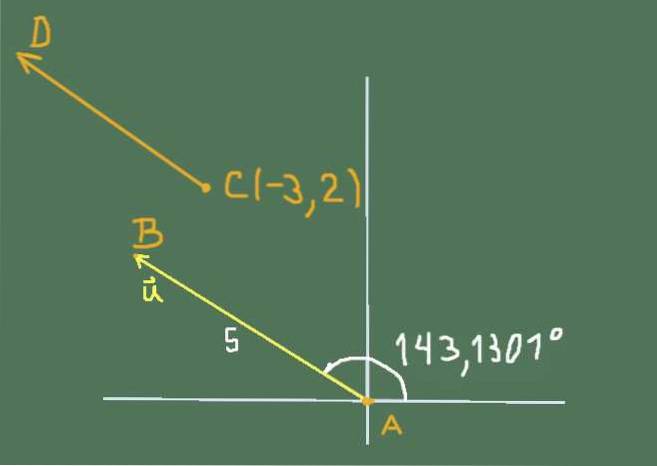
Les composantes cartésiennes de ou alors ils sont
ou alors = (5 * cos (143.1301º); 5 * sin (143.1301º))
Faire les calculs, il reste:
ou alors = (-4,3)
Les coordonnées de B sont inconnues donc nous placerons B (x, y)
Les coordonnées du vecteur UN B sont (x-0; y-0), mais comme u est une lentille d'équipe, l'égalité des composantes doit être remplie, il s'ensuit donc que les coordonnées de B sont (-4, 3).
De même les coordonnées du vecteur CD sont (x - (- 3)); (et - 2) qu'il doit être axé sur l'équipe u, lou conduisant à:
x + 3 = -4 et y -2 = 3
Alors les coordonnées du point D seront (-7, 5).
Les références
- Calculus.cc. Vecteur fixe. Vecteur libre. Récupéré de: calculo.cc
- Descartes 2d. Vecteurs fixes et vecteurs d'avion gratuits. Récupéré de: recursostic.educacion.es
- Projet Guao. Vecteurs teamlenses. Récupéré de: guao.org
- Resnick, R., Krane, K. (2001). La physique. New York: John Wiley & Sons.
- Serway, R.; Jewett, John W. (2004). Physique pour les scientifiques et les ingénieurs (6e éd.). Brooks / Cole.
- Tipler, Paul A. (2000). Physique pour la science et la technologie. Volume I. Barcelone: Ed. Reverté.
- Weisstein, E. «Vector». Dans Weisstein, Eric W. MathWorld. Recherche Wolfram.



Personne n'a encore commenté ce post.