Les vecteurs gratuits Ce sont ceux qui sont pleinement spécifiés par leur ampleur, leur direction et leur sens, sans qu'il soit nécessaire d'indiquer un point d'application ou une origine particulière.
Puisque des vecteurs infinis peuvent être dessinés de cette manière, un vecteur libre n'est pas une seule entité, mais un ensemble de vecteurs parallèles et identiques qui sont indépendants de l'endroit où ils se trouvent..
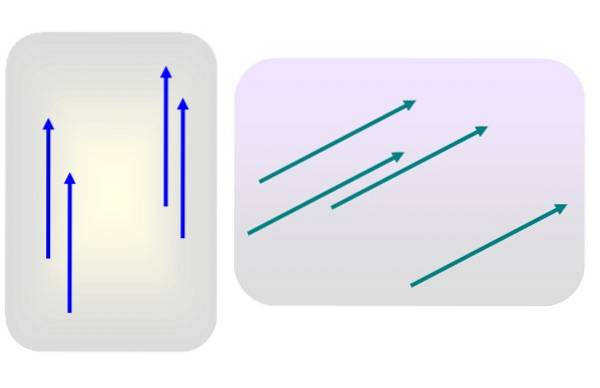
Disons que nous avons plusieurs vecteurs de magnitude 3 dirigés verticalement vers le haut, ou de magnitude 5 et inclinés vers la droite, comme sur la figure 1.
Aucun de ces vecteurs n'est spécifiquement appliqué à aucun moment. Alors l'un quelconque des vecteurs bleus ou verts est représentatif de leur groupe respectif, puisque leurs caractéristiques - module, direction et sens - ne changent pas du tout lorsqu'ils sont transférés à un autre endroit du plan..
Un vecteur libre est généralement indiqué dans le texte imprimé par une lettre en gras et minuscule, par exemple v. Ou avec des minuscules et une flèche en haut s'il s'agit d'un texte manuscrit.
Index des articles
L'avantage des vecteurs libres est qu'ils peuvent être déplacés dans le plan ou dans l'espace et conserver leurs propriétés, car tout représentant de l'ensemble est également valable..
C'est pourquoi, en physique et en mécanique, ils sont fréquemment utilisés. Par exemple, pour indiquer la vitesse linéaire d'un solide en mouvement, il n'est pas nécessaire de choisir un point particulier sur l'objet. Ainsi, le vecteur de vitesse se comporte comme un vecteur gratuit.
Un autre exemple de vecteur libre est la paire de forces. UNE paire Il se compose de deux forces d'amplitude et de direction égales, mais de directions opposées, appliquées en des points différents sur un solide. L'effet d'une paire n'est pas de translater l'objet, mais de provoquer une rotation grâce au moment produit.
La figure 2 montre un couple de forces appliquées à un volant. À travers les forces F1 Oui Fdeux, un couple est créé qui fait tourner le volant autour de son centre et dans le sens des aiguilles d'une montre.
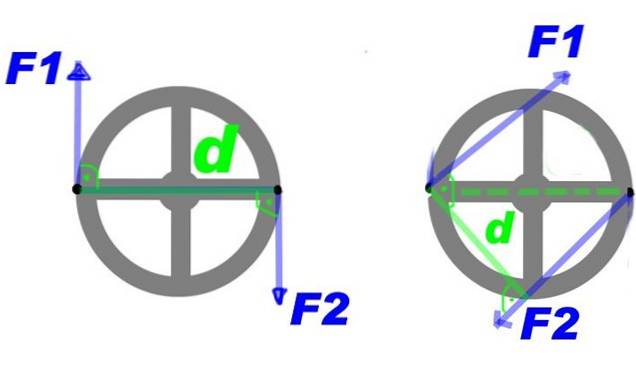
Vous pouvez apporter des modifications au couple et obtenir le même effet de rotation, par exemple en augmentant la force, mais en diminuant la distance entre eux. Ou maintenez la force et la distance, mais appliquez le couple sur une autre paire de points sur le volant, c'est-à-dire faites tourner le couple autour du centre.
Le moment de la paire de forces ou simplement paire, est un vecteur dont le module est Fd et est dirigé perpendiculairement au plan du volant. Dans l'exemple montré par convention, la rotation dans le sens des aiguilles d'une montre a un sens négatif.
Contrairement au vecteur libre v, les vecteurs UN B Oui CD ils sont fixes (voir figure 3), car ils ont un point de départ et un point d'arrivée spécifiés. Mais comme ils sont indulgents en équipe les uns avec les autres, et à leur tour avec le vecteur v, sont représentatifs du vecteur libre v.
Les principales propriétés des vecteurs libres sont les suivantes:
-Tout vecteur UN B (voir figure 2) est, comme dit, représentatif du vecteur libre v.
-Le module, la direction et le sens sont les mêmes chez tout représentant du vecteur libre. Dans la figure 2, les vecteurs UN B Oui CD représentent le vecteur libre v et ils sont axés sur l'équipe.
-Étant donné un point P dans l'espace, il est toujours possible de trouver un représentant du vecteur libre v dont l'origine est en P et ledit représentant est unique. C'est la propriété la plus importante des vecteurs libres et celle qui les rend si polyvalents.
-Un vecteur libre nul est noté 0 y est l'ensemble de tous les vecteurs qui manquent d'amplitude, de direction et de sens.
-Si le vecteur UN B représente un vecteur libre v, puis le vecteur BA représente un vecteur libre -v.
-La notation sera utilisée V3 pour désigner l'ensemble de tous les vecteurs libres de l'espace et Vdeux pour désigner tous les vecteurs libres de l'avion.
Avec des vecteurs libres, les opérations suivantes peuvent être effectuées:
-Somme
-Soustraction
-Multiplication du scalaire par un vecteur
-Produit scalaire entre deux vecteurs.
-Produit croisé entre deux vecteurs
-Combinaison linéaire de vecteurs
Et de plus.
Un élève essaie de nager d'un point sur la rive d'une rivière à un autre qui est juste en face. Pour y parvenir, rien directement à une vitesse de 6 km / h, dans une direction perpendiculaire, cependant le courant a une vitesse de 4 km / h qui le dévie.
Calculez la vitesse résultante du nageur et combien il est dévié par le courant.
La vitesse résultante du nageur est la somme vectorielle de sa vitesse (par rapport à la rivière, dessinée verticalement vers le haut) et de la vitesse de la rivière (dessinée de gauche à droite), qui est effectuée comme indiqué dans la figure ci-dessous:
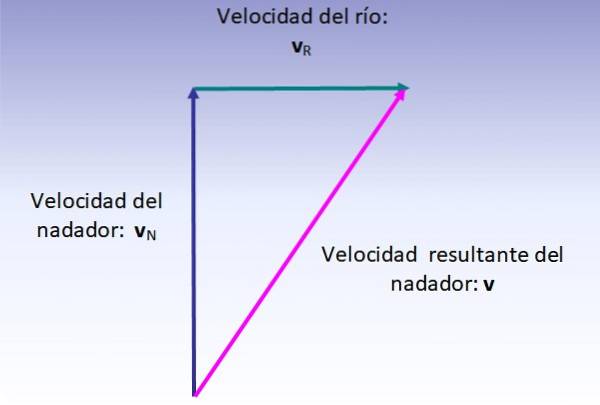
L'amplitude de la vitesse résultante correspond à l'hypoténuse du triangle rectangle représenté, donc:
v = (6deux + 4deux) ½ km / h = 7,2 km / h
La direction peut être calculée en utilisant l'angle par rapport à la perpendiculaire à la rive:
α = arcg (4/6) = 33,7 ° ou 56,3 ° par rapport à la rive.
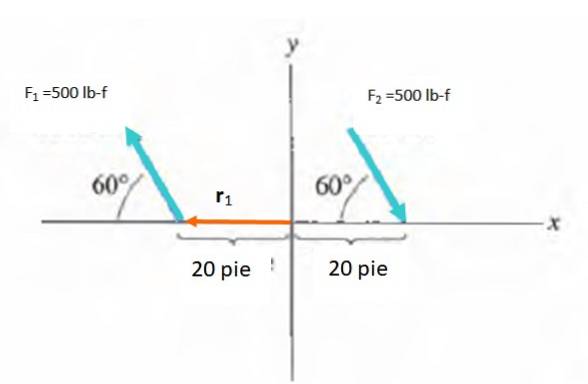
Trouvez le moment du couple montré dans la figure:
Le moment est calculé par:
M = r X F
Les unités du moment sont lb-f.ft. Le couple étant dans le plan de l'écran, le moment est dirigé perpendiculairement à celui-ci, soit vers l'extérieur, soit vers l'intérieur..
Comme le couple dans l'exemple a tendance à faire tourner l'objet sur lequel il est appliqué (ce qui n'est pas représenté sur la figure) dans le sens des aiguilles d'une montre, ce moment est considéré comme pointant vers l'intérieur de l'écran avec un signe négatif.
L'amplitude du moment est M = F.d. en a, où a est l'angle entre la force et le vecteur r. Vous devez choisir un point par rapport auquel calculer le moment, qui est un vecteur libre. L'origine du référentiel est choisie, donc r va de O au point d'application de chaque force.
M1 = Mdeux = -Fdsen60º = -500. 20 .sin 60º lb-f. pi = -8660,3 lb-f. le pied
Le moment net est la somme de M1 et Mdeux: -17329,5 lb-f. le pied.
Personne n'a encore commenté ce post.