La vitesse relative d'un objet est celui qui est mesuré par rapport à un observateur donné, puisqu'un autre observateur peut obtenir une mesure différente. La vitesse dépend toujours de l'observateur qui la mesure.
Par conséquent, la vitesse d'un objet mesurée par une certaine personne sera la vitesse relative par rapport à lui. Un autre observateur peut obtenir une valeur différente pour la vitesse, même s'il s'agit du même objet.
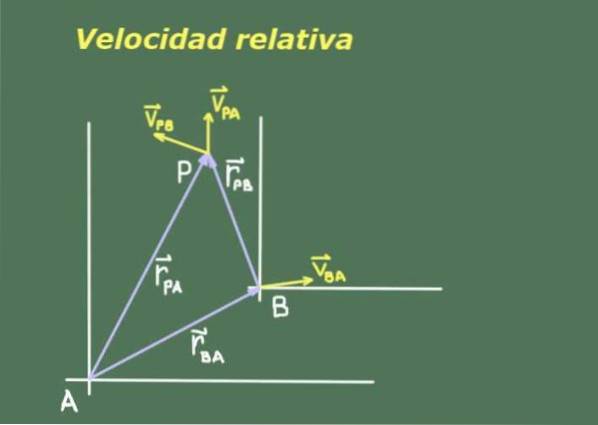
Puisque deux observateurs A et B se déplaçant l'un par rapport à l'autre peuvent avoir des mesures différentes d'un troisième objet mobile P, il est nécessaire de rechercher une relation entre les positions et les vitesses de P vues par A et B.
La figure 1 montre deux observateurs A et B avec leurs systèmes de référence respectifs, à partir desquels ils mesurent la position et la vitesse de l'objet P.
Chaque observateur A et B mesure la position et la vitesse de l'objet P à un instant donné t. En relativité classique (ou galiléenne), le temps pour l'observateur A est le même que pour l'observateur B indépendamment de leurs vitesses relatives.
Cet article traite de la relativité classique qui est valable et applicable à la plupart des situations quotidiennes dans lesquelles les objets ont des vitesses beaucoup plus lentes que celle de la lumière..
On note la position de l'observateur B par rapport à A comme rBA. Puisque la position est une quantité vectorielle, nous utilisons le gras pour l'indiquer. La position de l'objet P par rapport à A est notée rPennsylvanie et celle du même objet P par rapport à B rPB.
Index des articles
Il existe une relation vectorielle entre ces trois positions qui peut être déduite de la représentation de la figure 1:
rPennsylvanie= rPB + rBA
Si la dérivée de l'expression précédente est prise par rapport au temps t nous obtiendrons la relation entre les vitesses relatives de chaque observateur:
VPennsylvanie= VPB + VBA
Dans l'expression précédente on a la vitesse relative de P par rapport à A en fonction de la vitesse relative de P par rapport à B et de la vitesse relative de B par rapport à A.
De même, la vitesse relative de P par rapport à B peut s'écrire en fonction de la vitesse relative de P par rapport à A et de la vitesse relative de A par rapport à B.
VPB= VPennsylvanie + VUN B
Il est à noter que la vitesse relative de A par rapport à B est égale et contraire à celle de B par rapport à A:
VUN B = -VBA
Une voiture emprunte une route droite, qui va d'ouest en est, à une vitesse de 80 km / h tandis que dans la direction opposée (et de l'autre voie) une moto arrive à une vitesse de 100 km / h.
Un garçon se déplace sur la banquette arrière de la voiture qui veut connaître la vitesse relative d'une moto qui s'approche de lui. Pour trouver la réponse, l'enfant appliquera les relations qu'il vient de lire dans la section précédente, en identifiant chaque système de coordonnées comme suit:
-A est le système de coordonnées d'un observateur sur la route et par rapport à lui les vitesses de chaque véhicule ont été mesurées.
-B est la voiture et P est la moto.
Si vous souhaitez calculer la vitesse de la moto P par rapport à la voiture B, la relation suivante sera appliquée:
VPB= VPennsylvanie + VUN B=VPennsylvanie - VBA
En prenant la direction ouest-est comme positive, nous avons:
VPB= (-100 km / h - 80 km / h) je = -180 km / h je
Ce résultat est interprété comme suit: la moto se déplace par rapport à la voiture avec une vitesse de 180 km / h et une direction -je, c'est-à-dire d'est en ouest.
La moto et la voiture se sont croisées en suivant leur voie. L'enfant assis sur le siège arrière de la voiture voit la moto s'éloigner et veut maintenant savoir à quelle vitesse elle s'éloigne de lui, en supposant que la moto et la voiture maintiennent la même vitesse qu'avant la traversée..
Pour connaître la réponse, l'enfant applique la même relation que celle utilisée précédemment:
VPB= VPennsylvanie + VUN B=V Pennsylvanie - VBA
VPB= -100 km / h je - 80 km / h je = -180 km / h je
Et maintenant, la moto s'éloigne de la voiture avec la même vitesse relative à laquelle elle s'approchait avant de traverser..
La même moto de la partie 2 est renvoyée en conservant sa même vitesse de 100 km / h mais en changeant de direction. Autrement dit, la voiture (qui continue à une vitesse de 80 km / h) et la moto se déplacent toutes deux dans une direction positive est-ouest..
A un certain moment, la motocyclette dépasse la voiture, et l'enfant assis sur la banquette arrière de la voiture veut connaître la vitesse relative de la motocyclette par rapport à lui quand il la voit passer..
Pour obtenir la réponse, l'enfant applique à nouveau les relations de mouvement relatif:
VPB= VPennsylvanie + VUN B=VPennsylvanie - VBA
VPB= +100 km / h je - 80 km / h je = 20 km / h je
L'enfant de la banquette arrière regarde la moto dépasser la voiture à une vitesse de 20 km / h.
Un bateau à moteur traverse une rivière de 600 m de large et coule du nord au sud. La vitesse de la rivière est de 3 m / s. La vitesse du bateau par rapport à l'eau de la rivière est de 4 m / s vers l'est.
(i) Trouvez la vitesse du bateau par rapport à la rive du fleuve.
(ii) Indiquer la vitesse et la direction du bateau par rapport à la terre.
(iii) Calculer le temps de transition.
(iv) À quelle distance au sud il se sera déplacé à partir du point de départ.
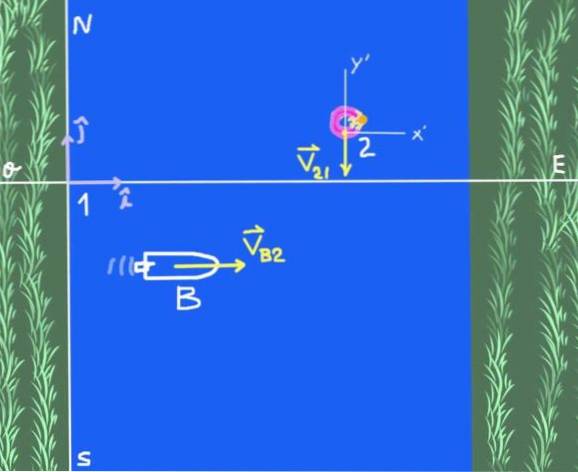
Il existe deux référentiels: le référentiel solidaire sur la rive que nous appellerons 1 et le référentiel 2, qui est un observateur flottant sur l'eau du fleuve. L'objet d'étude est le bateau B.
La vitesse du bateau par rapport à la rivière s'écrit sous forme vectorielle comme suit:
VB2 = 4 je Mme
La vitesse de l'observateur 2 (radeau sur la rivière) par rapport à l'observateur 1 (à terre):
Vvingt-et-un = -3 j Mme
Vous voulez trouver la vitesse du bateau par rapport à la terre VB1.
VB1 = VB2 + Vvingt-et-un
VB1 = (4 je - 3 j) Mme
La vitesse du bateau sera le module de la vitesse précédente:
|VB1| = (42 + (-3) 2) ½ = 5 m / s
Et l'adresse sera:
θ = arctan (-¾) = -36,87º
Le temps de traversée du bateau est le quotient entre la largeur de la rivière et la composante x de la vitesse du bateau par rapport à la terre.
t = (600 m) / (4 m / s) = 150 s
Pour calculer la dérive du bateau vers le sud, la composante y de la vitesse du bateau par rapport à la terre est multipliée par le temps de traversée:
ré = -3 j m / s * 150 s = -450 j m
Le déplacement vers le sud par rapport au point de départ est de 450m.
Personne n'a encore commenté ce post.