
Distribution du chi carré (χ²), comment la calculer, exemples
La preuve Chi au carré ou alors chi carré (χdeux, où χ est la lettre grecque appelée «chi») est utilisé pour déterminer le comportement d'une certaine variable et aussi lorsque vous voulez savoir si deux ou plusieurs variables sont statistiquement indépendantes.
Pour vérifier le comportement d'une variable, le test à effectuer est appelé test d'ajustement du chi carré. Pour savoir si deux ou plusieurs variables sont statistiquement indépendantes, le test est appelé chi carré de l'indépendance, aussi appelé contingence.
Ces tests font partie de la théorie de la décision statistique, dans laquelle une population est étudiée et des décisions sont prises à son sujet, en analysant un ou plusieurs échantillons prélevés sur elle. Cela nécessite de faire certaines hypothèses sur les variables, appelées hypothèse, qui peut ou peut ne pas être vrai.
Il existe des tests pour contraster ces conjectures et déterminer celles qui sont valides, dans une certaine marge de confiance, y compris le test du chi carré, qui peut être appliqué pour comparer deux ou plusieurs populations..
Comme nous le verrons, deux types d'hypothèses sont généralement soulevés à propos d'un paramètre de population dans deux échantillons: l'hypothèse nulle, appelée Hou alors (les échantillons sont indépendants), et l'hypothèse alternative, notée H1, (les échantillons sont corrélés) ce qui est l'opposé de cela.
Index des articles
- 1 Quand le test du chi carré est-il utilisé?
- 1.1 Conditions pour l'appliquer
- 2 Distribution du chi carré
- 2.1 Degrés de liberté
- 2.2 Formulation d'hypothèses
- 3 Comment la statistique du chi carré est-elle calculée?
- 3.1 Critères d'acceptation pour Ho
- 4 Exemple de calcul
- 5 Références
Quand le test du chi carré est-il utilisé?
Le test du chi carré est appliqué à des variables qui décrivent des qualités, telles que le sexe, l'état matrimonial, le groupe sanguin, la couleur des yeux et les préférences de divers types.
Le test est destiné lorsque vous souhaitez:
-Vérifier si une distribution est appropriée pour décrire une variable, qui est appelée qualité de l'ajustement. En utilisant le test du chi carré, il est possible de savoir s'il existe des différences significatives entre la distribution théorique choisie et la distribution de fréquence observée..
-Savoir si deux variables X et Y sont indépendantes du point de vue statistique. Ceci est connu comme test d'indépendance.
Puisqu'il est appliqué à des variables qualitatives ou catégorielles, le test du chi carré est largement utilisé en sciences sociales, en gestion et en médecine..
Conditions pour l'appliquer
Il y a deux conditions importantes pour l'appliquer correctement:
-Les données doivent être regroupées en fréquences.
-L'échantillon doit être suffisamment grand pour que la distribution du chi carré soit valide, sinon sa valeur est surestimée et conduit au rejet de l'hypothèse nulle alors que cela ne devrait pas être le cas..
La règle générale est que si une fréquence avec une valeur inférieure à 5 apparaît dans les données groupées, elle n'est pas utilisée. S'il y a plus d'une fréquence inférieure à 5, elles doivent être combinées en une seule pour obtenir une fréquence avec une valeur numérique supérieure à 5.
Distribution du chi carré
χdeux c'est une distribution continue de probabilités. En fait, il existe différentes courbes, en fonction d'un paramètre k appelé degrés de liberté de la variable aléatoire.
Ses propriétés sont:
-L'aire sous la courbe est égale à 1.
-Les valeurs de χdeux ils sont positifs.
-La distribution est asymétrique, c'est-à-dire qu'elle a un biais.
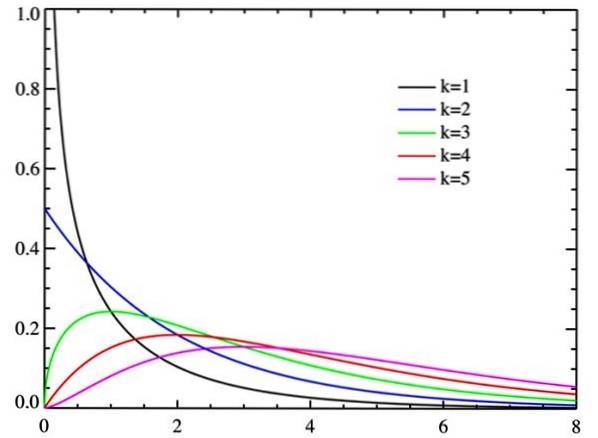
Degrés de liberté
Au fur et à mesure que les degrés de liberté augmentent, la distribution du chi carré tend vers la normalité, comme le montre la figure.
Pour une distribution donnée, les degrés de liberté sont déterminés par la tableau de contingence, qui est le tableau où sont enregistrées les fréquences observées des variables.
Si une table a F lignes et c colonnes, la valeur de k c'est:
k = (f - 1) ⋅ (c - 1)
Formulation d'hypothèses
Lorsque le test du chi carré est d'ajustement, les hypothèses suivantes sont formulées:
-Hou alors: la variable X a une distribution de probabilité f (x) avec les paramètres spécifiques y1, Ouideux…, Yp
-H1: X a une autre distribution de probabilité.
La distribution de probabilité supposée dans l'hypothèse nulle peut être, par exemple, la distribution normale connue, et les paramètres seraient la moyenne μ et l'écart type σ.
De plus, l'hypothèse nulle est évaluée avec un certain niveau de signification, c'est-à-dire une mesure de l'erreur qui serait commise en la rejetant étant vraie.
Habituellement, ce niveau est réglé sur 1%, 5% ou 10% et plus il est bas, plus le résultat du test est fiable..
Et si le test de contingence du chi carré est utilisé, qui, comme nous l'avons dit, sert à vérifier l'indépendance entre deux variables X et Y, les hypothèses sont:
-Hou alors: les variables X et Y sont indépendantes.
-H1: X et Y sont dépendants.
Encore une fois, il est nécessaire de spécifier un niveau de signification pour connaître la mesure de l'erreur lors de la prise de décision..
Comment la statistique du chi carré est-elle calculée?
La statistique du chi carré est calculée comme suit:

La sommation est effectuée de la première classe i = 1 à la dernière, qui est i = k.
En outre:
-Fou alors est une fréquence observée (provient des données obtenues).
-Fet est la fréquence attendue ou théorique (doit être calculée à partir des données).
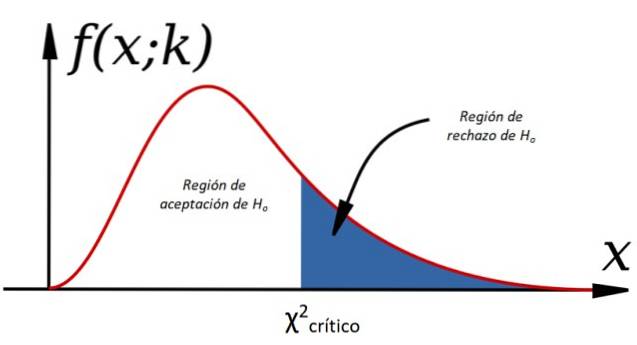
Pour accepter ou rejeter l'hypothèse nulle, on calcule χdeux pour les données observées et comparées à une valeur appelée chi carré critique, qui dépend des degrés de liberté k et le niveau de signification α:
χdeuxcritique = χdeuxk, α
Si, par exemple, nous voulons effectuer le test avec un niveau de signification de 1%, alors α = 0,01, si cela va être avec 5% alors α = 0,05 et ainsi de suite. Nous définissons p, le paramètre de la distribution, comme:
p = 1 - α
Ces valeurs critiques du chi carré sont déterminées par des tableaux contenant la valeur de surface cumulée. Par exemple, pour k = 1, qui représente 1 degré de liberté et α = 0,05, ce qui équivaut à p = 1- 0,05 = 0,95, la valeur de χdeux est 3841.

Critères d'acceptation Hou alors
Le critère d'acceptation de Hou alors c'est:
-Oui χdeux < χdeuxcritique H est acceptéou alors, sinon il est rejeté (voir figure 1).
Exemple de calcul
Dans l'application suivante, le test du chi carré sera utilisé comme test d'indépendance.
Supposons que les chercheurs veuillent savoir si la préférence pour le café noir est liée au sexe de la personne, et spécifiez la réponse avec un niveau de signification α = 0,05.
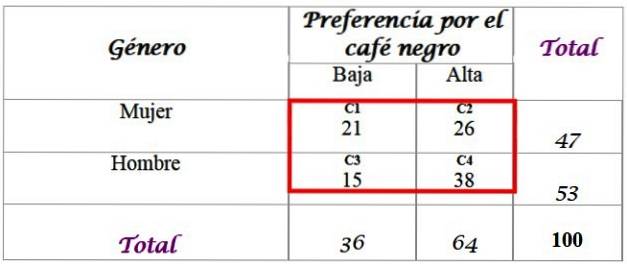
Pour cela, un échantillon de 100 personnes interrogées et leurs réponses sont disponibles:
Étape 1
Établissez les hypothèses:
-Hou alors: le sexe et la préférence pour le café noir sont indépendants.
-H1: le goût du café noir est lié au sexe de la personne.
Étape 2
Calculez les fréquences attendues pour la distribution, pour laquelle les totaux ajoutés dans la dernière ligne et dans la colonne de droite du tableau sont requis. Chaque cellule de la boîte rouge a une valeur attendue Fet, qui est calculé en multipliant le total de votre ligne F par le total de votre colonne C, divisé par le total de l'échantillon N:
Fet = (F x C) / N
Les résultats sont les suivants pour chaque cellule:
-C1: (36 x 47) / 100 = 16,92
-C2: (64 x 47) / 100 = 30,08
-C3: (36 x 53) / 100 = 19,08
-C4: (64 x 53) / 100 = 33,92
Étape 3
Ensuite, la statistique du chi carré doit être calculée pour cette distribution, selon la formule donnée:

Étape 4
Déterminer χdeuxcritique, sachant que les données enregistrées sont en f = 2 lignes et c = 2 colonnes, le nombre de degrés de liberté est donc:
k = (2-1) ⋅ (2-1) = 1.
Ce qui signifie qu'il faut chercher dans le tableau ci-dessus la valeur de χdeuxk, α = χdeux1; 0,05 , qui est:
χdeuxcritique = 3 841
Étape 5
Comparez les valeurs et décidez:
χdeux = 2,9005
χdeuxcritique = 3 841
Depuis χdeux < χdeuxcritique l'hypothèse nulle est acceptée et on conclut que la préférence pour le café noir n'est pas liée au sexe de la personne, avec un niveau de signification de 5%.
Les références
- Test du Chi Square pour l'indépendance. Récupéré de: saylordotorg.github.io.
- Med Wave. Statistiques appliquées aux sciences de la santé: le test du chi carré. Récupéré de: medwave.cl.
- Probabilités et statistiques. Test d'ajustement du chi carré. Récupéré de: probayestadistica.com.
- Triola, M. 2012. Statistiques élémentaires. 11ème. Édition. Addison Wesley.
- UNAM. Test du chi carré. Récupéré de: asesorias.cuautitlan2.unam.mx.

Personne n'a encore commenté ce post.