
Formules de coefficients de corrélation, calcul, interprétation, exemple
le Coefficient de corrélation en statistique, c'est un indicateur qui mesure la tendance de deux variables quantitatives X et Y à avoir une relation linéaire ou proportionnelle entre elles.
Généralement, les paires de variables X et Y sont deux caractéristiques d'une même population. Par exemple, X peut être la taille d'une personne et Y son poids..
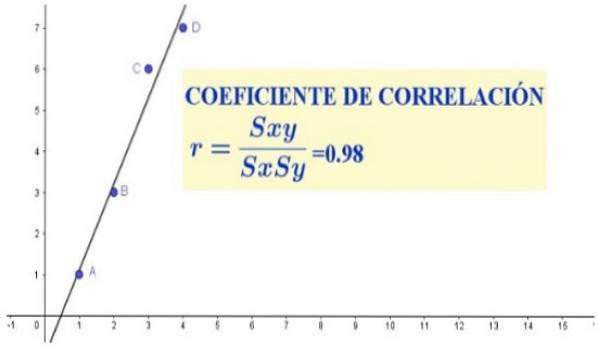
Dans ce cas, le coefficient de corrélation indiquerait s'il existe ou non une tendance à une relation proportionnelle entre la taille et le poids dans une population donnée..
Le coefficient de corrélation linéaire de Pearson est indiqué par la lettre r minuscules et ses valeurs minimale et maximale sont respectivement -1 et +1.
Une valeur r = +1 indiquerait que l'ensemble des paires (X, Y) sont parfaitement alignés et que lorsque X croît, Y croîtra dans la même proportion. Par contre, s'il arrivait que r = -1, l'ensemble des paires serait également parfaitement aligné, mais dans ce cas quand X augmente, Y diminue dans la même proportion.
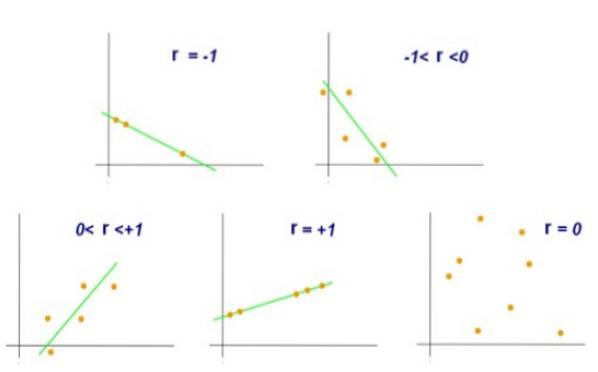
D'un autre côté, une valeur de r = 0 indiquerait qu'il n'y a pas de corrélation linéaire entre les variables X et Y. Alors qu'une valeur de r = +0,8 indiquerait que les paires (X, Y) ont tendance à se regrouper d'un côté et un autre d'une certaine hétéro.
La formule pour calculer le coefficient de corrélation r est la suivante:
Comment calculer le coefficient de corrélation?
Le coefficient de corrélation linéaire est une quantité statistique trouvée dans les calculatrices scientifiques, la plupart des feuilles de calcul et les programmes statistiques..
Cependant, il est pratique de savoir comment la formule qui la définit est appliquée, et pour cela un calcul détaillé sera affiché, effectué sur un petit ensemble de données.
Et comme il a été dit dans la section précédente, le coefficient de corrélation est la covariance Sxy divisée par le produit de l'écart type Sx pour les variables X et Sy pour la variable Y.
Covariance et variance
La covariance Sxy est:
Sxy = [Σ (Xi -
Où la somme va de 1 aux N paires de données (Xi, Yi).
Pour sa part, l'écart type de la variable X est la racine carrée de la variance de l'ensemble de données Xi, avec i de 1 à N:
Sx = √ [Σ (Xi -
De même, l'écart type de la variable Y est la racine carrée de la variance de l'ensemble de données Yi, avec i de 1 à N:
Sy = √ [Σ (Yi -
Cas illustratif
Afin de montrer en détail comment calculer le coefficient de corrélation, nous prendrons l'ensemble suivant de quatre paires de données
(X, Y): (1, 1); (2,3); (3, 6) et (4, 7).
Nous calculons d'abord la moyenne arithmétique pour X et Y, comme suit:
Ensuite, les paramètres restants sont calculés:
Covariance Sxy
Sxy = [(1 - 2,5) (1 - 4,25) + (2 - 2,5) (3 - 4,25) + (3 - 2,5) (6 - 4,25) +….…. (4 - 2,5) (7 - 4,25) ] / (4-1)
Sxy = [(-1,5) (- 3,25) + (-0,5) (- 1,25) + (0,5) (1,75) +… .
…. (1,5) (2,75)] / (3) = 10,5 / 3 = 3,5
Écart type Sx
Sx = √ [(-1,5)deux + (-0,5)deux + (0,5)deux + (1,5)deux) / (4-1)] = √ [5/3] = 1,29
Écart type Sy
Sx = √ [(-3,25)deux + (-1,25)deux + (1,75)deux + (2,75)deux) / (4-1)] =
√ [22,75 / 3] = 2,75
Coefficient de corrélation r
r = 3,5 / (1,29 * 2,75) = 0,98
Interprétation
Dans l'ensemble de données du cas précédent, une forte corrélation linéaire est observée entre les variables X et Y, qui se manifeste à la fois dans le nuage de points (illustré à la figure 1) et dans le coefficient de corrélation, qui a donné une valeur assez proche de l'unité.
Dans la mesure où le coefficient de corrélation est plus proche de 1 ou -1, plus il est logique d'ajuster les données à une ligne, résultat d'une régression linéaire..
Régression linéaire
La droite de régression linéaire est obtenue à partir de Méthode des moindres carrés. dans lequel les paramètres de la droite de régression sont obtenus à partir de la minimisation de la somme du carré de la différence entre la valeur Y estimée et le Yi des N données.
Par contre, les paramètres a et b de la droite de régression y = a + bx, obtenus par la méthode des moindres carrés, sont:
* b = Sxy / (Sxdeux) Pour la pente
* a =
Rappelons que Sxy est la covariance définie ci-dessus et Sxdeux est la variance ou le carré de l'écart type défini ci-dessus.
Exemple
Le coefficient de corrélation est utilisé pour déterminer s'il existe une corrélation linéaire entre deux variables. Elle est applicable lorsque les variables à étudier sont quantitatives et, en outre, on suppose qu'elles suivent une distribution de type normale..
Nous avons un exemple illustratif ci-dessous: une mesure du degré d'obésité est l'indice de masse corporelle, qui est obtenu en divisant le poids d'une personne en kilogrammes par la hauteur au carré de la même en unités de mètres carrés.
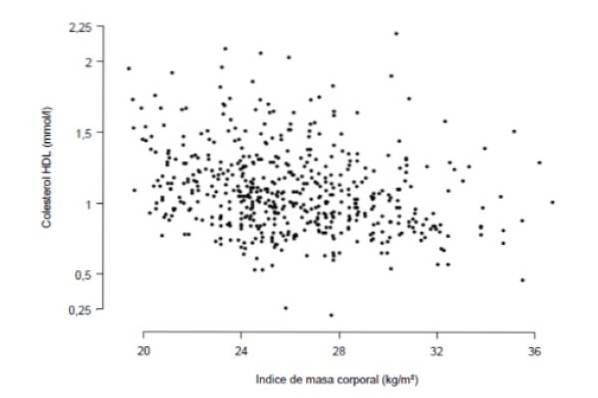
Vous voulez savoir s'il existe une forte corrélation entre l'indice de masse corporelle et la concentration de cholestérol HDL dans le sang, mesurée en millimoles par litre. A cet effet, une étude auprès de 533 personnes a été réalisée, qui est résumée dans le graphique suivant, dans lequel chaque point représente les données d'une personne.

Une observation attentive du graphique montre qu'il existe une certaine tendance linéaire (peu marquée) entre la concentration de cholestérol HDL et l'indice de masse corporelle. La mesure quantitative de cette tendance est le coefficient de corrélation, qui pour ce cas s'est avéré être r = -0,276.
Les références
- González C. Statistiques générales. Récupéré de: tarwi.lamolina.edu.pe
- IACS. Institut aragonais des sciences de la santé. Récupéré de: ics-aragon.com
- Salazar C. et Castillo S. Principes de base de la statistique. (2018). Récupéré de: dspace.uce.edu.ec
- Superprof. Coefficient de corrélation. Récupéré de: superprof.es
- USAC. Manuel de statistiques descriptives. (2011). Récupéré de: statistics.ingenieria.usac.edu.gt
- Wikipédia. Coefficient de corrélation de Pearson. Récupéré de: es.wikipedia.com.


Personne n'a encore commenté ce post.